您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹了C#中算法的實例詳解,具有一定借鑒價值,感興趣的朋友可以參考下,希望大家閱讀完這篇文章之后大有收獲,下面讓小編帶著大家一起了解一下。
給出以下表達式的值:
a. (0 + 15) / 2
b. 2.0e-6 * 100000000.1
c. true && false || true && true
a.7
b.1562500.0015625
c.True
static void Main(string[] args)
{int a = (0 + 15) / 2;double b = Math.Pow(2.0, -6) * 100000000.1; //Math.Pow(double x, double y) 求x的y次方bool c = true && false || true && true;//Console.WriteLine 向控制臺窗口輸出一行Console.WriteLine($"a.{a}");
Console.WriteLine($"b.{b}");
Console.WriteLine($"c.{c}");
}給出以下表達式的類型和值:
a. (1 + 2.236) / 2
b. 1 + 2 + 3 + 4.0
c. 4.1 >= 4
d. 1 + 2 + "3"
Name Type Value
a System.Double 1.618
b System.Double 10
c System.Boolean True
d System.String 33
static void Main(string[] args)
{//var 變量名 = 初始值 根據初始值自動判斷變量類型var a = (1 + 2.236) / 2;var b = 1 + 2 + 3 + 4.0;var c = 4.1 >= 4;var d = 1 + 2 + "3";//Console.WriteLine 向控制臺輸出一行//變量名.GetType() 返回變量類型//Type.ToString() 將類型名轉換為字符串Console.WriteLine("\tName\tType \tValue");
Console.WriteLine($"\ta\t{a.GetType().ToString()}\t{a}");
Console.WriteLine($"\tb\t{b.GetType().ToString()}\t{b}");
Console.WriteLine($"\tc\t{c.GetType().ToString()}\t{c}");
Console.WriteLine($"\td\t{d.GetType().ToString()}\taegqsqibtmh");
}編寫一個程序,從命令行獲取三個整數參數。
如果它們都相等則打印 equal,
否則打印 not equal。
簡單的 if 判斷即可
static void Main(string[] args)
{//Console.ReadLine() 從控制臺讀入一整行(返回int)//string.Split(char) 根據提供的分隔符將字符串分割,返回字符串數組//Int32.Parse(string) 將字符串轉換為相應的整型數據string input = Console.ReadLine();int a = Int32.Parse(input.Split(' ')[0]);int b = Int32.Parse(input.Split(' ')[1]);int c = Int32.Parse(input.Split(' ')[2]);//Console.WriteLine() 向控制臺輸出一行if (a == b && b == c)
{
Console.WriteLine("equal");
}else{
Console.WriteLine("not equal");
}
}下列語句各有什么問題(如果有的話)?
a. if (a > b) then c = 0;
b. if a > b { c = 0; }
c. if (a > b) c = 0;
d. if (a > b) c = 0 else b = 0;
a. if 后跟 then 的語法不能在 C# 中使用。
b. if 后的判斷語句需要在括號內。
c. 正確,只有一條語句時大括號可以省略。
d. c = 0 后缺少分號。
static void Main(string[] args)
{int a = 1;int b = 2;int c = 0;//if (a > b) then c = 0; //if 后不能跟 then//if a > b { c = 0; } //if后必須跟括號if (a > b) c = 0;//正確//if (a > b) c = 0 else b = 0; //c = 0后缺少分號}編寫一段程序,
如果 double 類型的變量 x 和 y 都嚴格位于 0 和 1 之間則打印 true
否則打印 false。
比較簡單,直接判斷即可。
static void Main(string[] args)
{//修改這兩個值進行測試double x = 0.05;double y = 0.01;if (x > 0 && x < 1 && y > 0 && y < 1)
{
Console.WriteLine("true");
}else{
Console.WriteLine("false");
}
}下面這段程序會打印出什么?
輸出斐波那契數列。
將書中的代碼直接實現即可。
//輸出斐波那契數列static void Main(string[] args)
{int f = 0;int g = 1;for (int i = 0; i <= 15; i++)
{//Console.WriteLine與StdOut.println功能相同//實現向控制臺輸出一行 Console.WriteLine(f);
f = f + g;
g = f - g;
}
}分別給出以下代碼段打印出的值。
同上題,直接實現即可。
a
3.00009
double計算存在誤差,并不精確。
b
499500
1000 + 999 + 998……
c
10000
1000 * 10,外層循環的結束條件為 2i > 1000。
private static void a()
{
Console.WriteLine("a");double t = 9.0;while (Math.Abs(t - 9.0 / t) > .001)
{
t = (9.0 / t + t) / 2.0;
}
Console.Write($"{t:N5}\n");//:N5代表保留5位小數,同理可使用N1、N2…… }private static void b()
{
Console.WriteLine("\nb");int sum = 0;for (int i = 1; i < 1000; i++)
{for (int j = 0; j < i; j++)
{
sum++;
}
}
Console.WriteLine(sum);
}private static void c()
{
Console.WriteLine("\nc");int sum = 0;for (int i = 1; i < 1000; i *= 2)
{for (int j = 0; j < 1000; j++)
{
sum++;
}
}
Console.WriteLine(sum);
}static void Main(string[] args)
{//a double 計算存在誤差 a();//b 1000+999+998…… b();//c 由于2^10 = 1024 > 1000,最終sum = 1000 * 10 = 10000 c();
}下列語句會打印出什么結果?給出解釋。
b
197
e
static void Main(string[] args)
{
Console.WriteLine('b');
Console.WriteLine('b' + 'c'); //char 被隱式轉為為 int 類型,取 ascii 碼Console.WriteLine((char)('a' + 4)); //強制轉換后,ascii 碼被轉換為相應的字符}編寫一段代碼,將一個正整數N用二進制表示并轉換為一個 String 類型的值 s。
有兩種方法,要么直接調用庫函數,要么用書中給出的代碼轉換。
static void Main(string[] args)
{int N = 4;//1.直接轉換 Convert.ToString(int, int) 第一個為要轉換的數,第二個為要轉換的進制Console.WriteLine($"{Convert.ToString(N, 2)}");//2.轉換為二進制數string s = "";for (int n = N; n > 0; n /= 2)
{
s = (n % 2) + s;
}
Console.WriteLine(s);
}下面這段代碼有什么問題?
變量使用前需要先賦值。
static void Main(string[] args)
{int[] a;for (int i = 0; i < 10; i++)
{
a[i] = i * i; //不允許使用未賦值的局部變量 }
}編寫一段代碼,打印出一個二維布爾數組的內容。
其中,使用 * 表示真,空格表示假,打印出行號和列號。
注意,二維數組 bool[M, N] 代表 M 行 N 列的布爾數組。
使用二重循環即可實現。
輸出使用制表符 ’\t’ 作為分隔。
static void PrintArray2D(bool[,] array)
{int rows = array.GetLength(0);//獲取行數int columns = array.GetLength(1);//獲取列數//輸出列號for (int i = 0; i < columns; i++)
{
Console.Write($"\t{i + 1}");
}
Console.Write("\n");for (int i = 0; i < rows; i++)
{//輸出行號Console.Write($"{i + 1}");for (int j = 0; j < columns; j++)
{if (array[i, j])
{
Console.Write($"\t*");
}else{
Console.Write($"\t ");
}
}
Console.Write("\n");
}
}以下代碼段會打印出什么結果?
第一個循環初始化數組{9, 8, 7, 6, 5, 4, 3, 2, 1, 0}
第二個循環用相應位置的值作為下標取值,例如:a[0] = a[a[0]] = a[9] = 0
最后結果為:0,1,2,3,4,4,3,2,1,0
static void Main(string[] args)
{int[] a = new int[10];for (int i = 0; i < 10; i++)
{
a[i] = 9 - i;
}//a[10] = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0}for (int i = 0; i < 10; i++)
{
a[i] = a[a[i]];
}//a[0] = a[9] = 0; a[1] = a[8] = 1; a[2] = a[7] = 2;......for (int i = 0; i < 10; i++)
{
Console.WriteLine(a[i]);
}
}編寫一段代碼,打印出一個 M 行 N 列的二維數組的轉置。
轉置輸出只需要在二重循環的時候將行、列輸出順序取反即可。
static void Main(string[] args)
{int M = 2;int N = 3;int[,] array = new int[M, N];//新建一個二維數組for (int i = 0; i < M; i++)
{for (int j = 0; j < N; j++)
{
array[i, j] = i + j;
}
}
Console.WriteLine("Origin");
PrintArray2D(array, M, N);
Console.WriteLine("Transposed");
PrintArrayTranspose2D(array, M, N);
}//轉置輸出private static void PrintArrayTranspose2D(int[,] array, int rows, int columns)
{//交換行、列輸出順序for (int i = 0; i < columns; i++)
{for (int j = 0; j < rows; j++)
{
Console.Write($"\t{array[j, i]}");
}
Console.Write("\n");
}
}//正常輸出private static void PrintArray2D(int[,] array, int rows, int columns)
{for (int i = 0; i < rows; i++)
{for (int j = 0; j < columns; j++)
{
Console.Write($"\t{array[i, j]}");
}
Console.Write("\n");
}
}編寫一個靜態方法lg(),接受一個整型參數N,返回不大于log2(N)的最大整數。
不要使用 Math 庫。
簡單使用 log 的定義逼近即可。
static void Main(string[] args)
{int N = 9;
Console.WriteLine($"{ lg(N)}");
}//利用循環逼近 N,得到 log2(N) 的值static int lg(int N)
{int baseNumber = 2;int pow = 1;int sum = 2;for (pow = 1; sum < N; ++pow)
{
sum *= baseNumber;
}return pow - 1;
}編寫一個靜態方法 histogram(),
接受一個整型數組 a[] 和一個整數 M 作為參數并返回一個大小為 M 的數組,
其中第 i 個元素的值為整數 i 在參數數組中出現的次數。
如果 a[] 中的值均在 0 到 M-1 之間,
返回數組中所有元素之和應該和 a.length 相等。
利用二重循環,查找每個值在數組中出現的次數。
static void Main(string[] args)
{int[] a = new int[10];int M = 10;for (int i = 0; i < 10; ++i)
{
a[i] = i;
}int[] result = Histogram(a, M);
Console.WriteLine($"a.length: {a.Length}");
Console.WriteLine($"sum of result array: {result.Sum()}");
}static int[] Histogram(int[] a, int M)
{int[] result = new int[M];for (int i = 0; i < M; ++i)
{//初始化result[i] = 0;//遍歷數組,計算數組中值為 i 的元素個數for (int j = 0; j < a.Length; ++j)
{if (a[j] == i) //值為 i 的元素 {
result[i]++;
}
}
}return result;
}給出 exR1(6) 的返回值。
填入代碼測試即可。
用字符串拼接的方式展示遞歸。
類似于這個:

static void Main(string[] args)
{
Console.WriteLine($"{exR1(6)}");
}//exR1(6) = //exR1(3) + 6 + exR1(4) + 6//exR1(0) + 3 + exR1(1) + 3 + 6 + exR1(4) + 6//"" + 3 + exR1(-2) + 1 + exR1(-1) + 1 + 3 + 6 + exR1(4) + 6//"" + 3 + "" + 1 + "" + 1 + 3 + 6 + exR1(4) + 6//"31136" + exR1(4) + 6//......public static string exR1(int n)
{if (n <= 0)
{return "";
}return exR1(n - 3) + n + exR1(n - 2) + n;
}找出以下遞歸函數的問題:
public static String exR2(int n)
{
String s = exR2(n - 3) + n + exR2(n - 2) + n; if (n <= 0) return ""; return s;
}書中已經給出了解釋。
遞歸時結束條件必須放在遞歸語句的前面,否則會不斷展開而無法結束。
static void Main(string[] args)
{
Console.WriteLine($"{exR2(6)}");//拋出 StackOverflow Exception }public static string exR2(int n)
{string s = exR2(n - 3) + n + exR2(n - 2) + n;//運行到 exR2 即展開,不會再運行下一句if (n <= 0) return "";return s;
}請看以下遞歸函數:
public static int mystery(int a, int b)
{if (b == 0) return 0;if (b % 2 == 0) return mystery(a + a, b / 2);return mystery(a + a, b / 2) + a;
}mystery(2, 25) 和 mystery(3, 11) 的返回值是多少?
給定正整數 a 和 b,mystery(a, b) 計算的結果是什么?
將代碼中的 + 替換為 * 并將 return 0 改為 return 1,然后回答相同的問題。
其實就是一種快速乘法的實現,換成乘號之后就變成了快速乘冪。
例如對于乘法 2 * 4,可以用 2 + 2 + 2 + 2 做四次加法計算;也可以變為 (2 + 2) * 2 = (2 + 2) + (2 + 2) 的形式,用兩次加法就可以完成(先計算 2 + 2 的值,再計算 4 + 4 的值)。
同理對于乘冪 28,既可以用 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 做 8 次乘法,也可以只用三次乘法就計算出來:
22 = 2 * 2
24 = 22 * 22
28 = 24 * 24
這樣時間復雜度就從 O(n) 變為了 O(log n)。
static void Main(string[] args)
{
Console.WriteLine($"mystery(2, 25): {mystery(2, 25)}");
Console.WriteLine($"mystery(3, 11): {mystery(3, 11)}");
Console.WriteLine($"mysteryChanged(2, 8): {mysteryChanged(2, 8)}");
Console.WriteLine($"mysteryChanged(3, 2): {mysteryChanged(3, 2)}");
}//mystery(a, b) = a * b//利用等式:a * b = 2a * b/2 = (2a * (b-1) / 2) + a//示例://mystery(2, 25) =//mystery(2 + 2, 12) + 2 =//mystery(4 + 4, 6) + 2 =//mystery(8 + 8, 3) =//mystery(16 + 16, 1) + 16 + 2 =//mystery(32 + 32, 0) + 32 + 16 + 2 =//0 + 32 + 16 + 2 =//50public static int mystery(int a, int b)
{if (b == 0) return 0;if (b % 2 == 0) return mystery(a + a, b / 2);return mystery(a + a, b / 2) + a;
}//mysteryChanged(a, b) = a ^ b//同理(乘方與乘法,乘法與加法之間具有類似的性質)//a ^ b = (a ^ 2) ^ (b / 2) = (a ^ 2) ^ ((b - 1) / 2) * apublic static int mysteryChanged(int a, int b)
{if (b == 0) return 1;if (b % 2 == 0) return mysteryChanged(a * a, b / 2);return mysteryChanged(a * a, b / 2) * a;
}在計算機上運行以下程序:
public class Fibnacci
{public static long F(int N)
{if (N == 0) return 0;if (N == 1) return 1;return F(N - 1) + F(N - 2);
}public static void main(String[] args)
{for (int N = 0; N < 100; N++)
StdOut.println(N + " " + F(N));
}
}計算機用這段程序在一個小時之內能夠得到 F(N) 結果的最大 N 值是多少?
開發 F(N) 的一個更好的實現,用數組保存已經計算過的值。
普通的遞歸算法效率很低,原因是越到后面重復運算的數目越多。
比如:
F(2) = F(1) + F(0)
F(3) = F(2) + F(1) = F(1) + F(1) + F(0)
可以看到 F(1) 被重復計算了兩次。
改進的方式是將每次運算的結果保存在數組中,之后計算過的數據直接從數組中提取。
class Fibnacci
{//long 類型不夠大,換成 UINT64 類型//用于保存計算結果的數組,UInt64? 代表可以賦值為普通 UInt64 類型的值以及 null 值private static UInt64?[] fibnacciResults = new UInt64?[100]; static void Main(string[] args)
{/* * 測試環境
*
* Surface Pro3 i7
* i7 4650U + 8G
*
*/Stopwatch timer = Stopwatch.StartNew();for (int N = 0; N < 100; ++N)
{//書本中的代碼,非常慢,1小時后 N = 50//Console.WriteLine($"{N} {F(N)}");//利用已知結果加速//全部計算完畢耗時 84msConsole.WriteLine($"{N} {BetterF(N)}");
}
Console.WriteLine($"{timer.ElapsedMilliseconds} ms");
}//書中提供的代碼public static UInt64 F(int N)
{if (N == 0)return 0;if (N == 1)return 1;return F(N - 1) + F(N - 2);
}//更好的實現,將已經計算的結果保存,不必重復計算public static UInt64? BetterF(int N)
{if (N == 0)return 0;if (N == 1)return 1;if (fibnacciResults[N] != null) //如果已經計算過則直接讀取已知值 {return fibnacciResults[N];
}else{
fibnacciResults[N] = BetterF(N - 1) + BetterF(N - 2);return fibnacciResults[N];
}
}
}編寫一個遞歸的靜態方法計算 ln(N!) 的值。
根據對數的性質可以得到:
ln(N!) = ln(N) + ln(N – 1) + ln(N – 2)…
static void Main(string[] args)
{int N = 4;
Console.WriteLine($"{factorialLn(N)}");
}//ln(N!) =//ln(N * (N - 1) * ... * 1) =//ln(N) + ln((N - 1)!)public static double factorialLn(int N)
{if (N == 1)
{return 0;
}return Math.Log(N) + factorialLn(N - 1);
}編寫一段程序,從標準輸入按行讀取數據,其中每行都包含一個名字和兩個整數。
然后用 printf() 打印一張表格,
每行的若干列數據包含名字、兩個整數和第一個整數除以第二個整數的結果,
精確到小數點后三位。
可以用這種程序將棒球球手的擊球命中率或者學生的考試分數制成表格。
實現上沒什么難度,打印表格的部分可以參考之前打印二位布爾數組的方法。
注意整型數據之間相除得到的仍然是整型,小數部分會直接舍去,例如 2 / 3 = 0。
static void Main(string[] args)
{int columns = 2;int rows = int.Parse(Console.ReadLine()); //行號string[] names = new string[rows]; //姓名int[,] array = new int[rows, columns]; //輸入的兩個整數double[] results = new double[rows]; //計算結果for (int i = 0; i < rows; ++i)
{string temp = Console.ReadLine();
names[i] = temp.Split(' ')[0];for (int j = 0; j < columns; ++j)
{
array[i, j] = int.Parse(temp.Split(' ')[j + 1]);
}
results[i] = (double)array[i, 0] / array[i, 1];
}
PrintArray2D(names, array, results);
}static void PrintArray2D(string[] names, int[,] array, double[] results)
{int rows = array.GetLength(0);//獲取行數int columns = array.GetLength(1);//獲取列數for (int i = 0; i < rows; i++)
{
Console.Write($"\t{names[i]}");for (int j = 0; j < columns - 1; j++)
{
Console.Write($"\t{array[i, j]}");
}
Console.Write($"\t{array[i, columns - 1]}");
Console.Write($"\t{results[i]:N3}"); //變量名:N3 保留三位小數Console.Write("\n");
}
}使用 1.1.6.4 節中的 rank() 遞歸方法重新實現 BinarySearch 并跟蹤該方法的調用。
每當該方法被調用時,打印出它的參數 lo 和 hi 并按照遞歸的深度縮進。
提示:為遞歸方法添加一個參數來保存遞歸的深度。
按照書中的提示增加一個保存深度的參數。
class BinarySearch
{static void Main(string[] args)
{int[] array = new int[10] { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
rank(9, array);
}//重載方法,用于啟動二分查找public static int rank(int key, int[] a)
{return rank(key, a, 0, a.Length - 1, 1);
}//二分查找public static int rank(int key, int[] a, int lo, int hi, int number)
{for (int i = 0; i < number; ++i)
{
Console.Write(" ");
}
Console.WriteLine($"{number}: {lo} {hi}");if (lo > hi)
{return -1;
}int mid = lo + (hi - lo) / 2;if (key < a[mid])
{return rank(key, a, lo, mid - 1, number + 1);
}else if (key > a[mid])
{return rank(key, a, mid + 1, hi, number + 1);
}else{return mid;
}
}
}為 BinarySearch 的測試用例添加一個參數:
+ 打印出標準輸入中不在白名單上的值;
- 則打印出標準輸入中在白名單上的值。
在主函數里做一下判斷就可以了,加號則輸出所有找不到的值,減號則相反。
static void Main(string[] args)
{//從largeW.txt中讀取數據string[] whiteList = File.ReadAllLines("largeW.txt");int[] WhiteList = new int[whiteList.Length]; for (int i = 0; i < whiteList.Length; ++i)
{
WhiteList[i] = int.Parse(whiteList[i]);
}
Array.Sort<int>(WhiteList);
Console.WriteLine("Type the numbers you want to query: ");//輸入樣例:5 824524 478510 387221string input = Console.ReadLine();int[] Query = new int[input.Split(' ').Length];for (int i = 0; i < Query.Length; ++i)
{
Query[i] = int.Parse(input.Split(' ')[i]);
}
Console.WriteLine("Type '+' to get the numbers that not in the whitelist," + "'-' to get the numbers that in the whitelist.");char operation = Console.ReadLine()[0];foreach (int n in Query)
{if (rank(n, WhiteList) == -1)
{if (operation == '+')
{
Console.WriteLine(n);
}
}else if (operation == '-')
{
Console.WriteLine(n);
}
}
}//重載方法,用于啟動二分查找public static int rank(int key, int[] a)
{return rank(key, a, 0, a.Length - 1);
}//二分查找public static int rank(int key, int[] a, int lo, int hi)
{if (lo > hi)
{return -1;
}int mid = lo + (hi - lo) / 2;if (key < a[mid])
{return rank(key, a, lo, mid - 1);
}else if (key > a[mid])
{return rank(key, a, mid + 1, hi);
}else{return mid;
}
}給出使用歐幾里得算法計算 105 和 24 的最大公約數的過程中得到的一系列 p 和 q 的值。
擴展該算法中的代碼得到一個程序 Euclid,從命令行接受兩個參數,
計算它們的最大公約數并打印出每次調用遞歸方法時的兩個參數。
使用你的程序計算 1111111 和 1234567 的最大公約數。
在書本中 GCD 的基礎上,在函數開始時增加一條輸出語句即可。
static void Main(string[] args)
{
GCD(105, 24);
Console.WriteLine();
GCD(111111, 1234567);
}public static int GCD(int a, int b)
{
Console.WriteLine($"{a} {b}");if (b == 0)
{return a;
}return GCD(b, a % b);
}用數學歸納法證明歐幾里得算法能夠計算出任意一對非負整數 p 和 q 的最大公約數
證明見代碼。
也可以訪問維基百科:輾轉相除法
namespace _1._1._25
{/* * 1.1.25
*
* 用數學歸納法證明歐幾里得算法能夠計算出任意一對非負整數 p 和 q 的最大公約數
*
*/class Program
{static void Main(string[] args)
{/* 證明:
*
* 已知: a, b 皆為正整數,且 a > b。g 是 a、b 的最大公約數
* 設 r0 = a % b, rk = rk-2 % rk-1
* 那么有 gcd(a, b) = gcd(b, r0) = gcd(r0, r1)... = gcd(rn-1, rn)
* 且 rn = 0 (此時算法終止)
*
* 由于 rn-2 = qn * rn - 1 + rn = qn * rn-1 (qn = [rn-2 / rn-1] []代表向下取整)
* 可得 rn-2 能被 rn-1 整除
* 則
* rn-3 = qn-1 * rn-2 + rn-1
* = qn-1 * (qn * rn-1) + rn-1 (代入 rn-2 = qn * rn-1)
* = qn-1 * qn * rn-1 + rn-1
* = (qn-1 * qn + 1) * rn-1
* 可得 rn-3 也能被 rn-1 整除
* 以此類推,rn-1 可以整除 a 和 b,即 rn-1 是 a 和 b 的公約數
* 則 rn-1 <= g
*
* 因為 g 是 a、b 的最大公約數,由性質可得:
* a = mg, b = ng (m、n 是自然數)
*
* r0
* = a % b
* = a - q0 * b (q0 = [a / b] []代表向下取整)
* = mg - q0 * ng (代入 34 行的結論)
* = (m - q0 * n)g
*
* 可得 r0 能被 g 整除
* 同理 r1, r2, r3, ..., rn-1 都可以被 g 整除
* 因此 g <= rn-1
*
* 綜合 31 行和 44 行的結論可得 rn-1 = g
*
* 證明完畢 */}static int gcd(int p, int q)
{if (q == 0)
{return p;
}int r = p % q;return gcd(q, r);
}
}
}將三個數字排序。
假設 a、b、c 和 t 都是同一種原始數字類型的變量。
證明如下代碼能夠將 a、b、c 按照升序排列。
if (a > b) { t = a; a = b; b = t; }if (a > c) { t = a; a = c; c = t; }if (b > c) { t = b; b = c; c = t; }見代碼部分。
static void Main(string[] args)
{int a = 3;int b = 2;int c = 1;int t = 0;if (a > b) { t = a; a = b; b = t; } //如果 a > b,那么 a, b 交換,保證b >= aif (a > c) { t = a; a = c; c = t; } //如果 b >= a > c,那么 a, c 交換,保證 c >= aif (b > c) { t = b; b = c; c = t; } //如果 b > c >= a,那么 b, c 交換,保證 c >= bConsole.WriteLine($"{a} {b} {c}"); //最終結果為 c >= b >= a,保證升序排列}二項分布。
估計用以下代碼計算 binomial(100, 50, 0.25) 將會產生的遞歸調用次數:
public static double binomial(int N, int k, double p)
{if (N == 0 && k == 0) return 1.0;if (N < 0 || k < 0) return 0.0;return (1.0 - p) * binomial(N - 1, k, p) + p * binomial(N - 1, k - 1, p);
}將已經計算過的值保存在數組中并給出一個更好的實現。
與之前的斐波那契數列類似,都是重復計算的問題。
7751次。
class Program
{static int BinomialCalled = 0; //計算遞歸調用次數static double?[,] BinomialCache; //保存計算結果的數組static void Main(string[] args)
{
BinomialCache = new double?[101, 51];
Console.WriteLine(Binomial(100, 50, 0.25));
Console.WriteLine(BinomialCalled);
}public static double? Binomial(int N, int k, double p)
{
BinomialCalled++;if (N == 0 && k == 0)return 1.0;if (N < 0 || k < 0)return 0.0;if (BinomialCache[N, k] != null)
{return BinomialCache[N, k];
}else{
BinomialCache[N, k] = (1.0 - p) * Binomial(N - 1, k, p) + p * Binomial(N - 1, k - 1, p);return BinomialCache[N, k];
}
}
}刪除重復元素。
修改 BinarySearch 類中的測試用例來刪去排序之后白名單中的所有重復元素。
實現方法有很多,這里是使用一個 HashSet 做中轉,刪除所有的重復元素。
也可以使用 Linq 里的 Distinct() 方法,
也可以排序后直接遍歷一遍,遇到相同的就刪除,遇到不同的就保存起來用于之后的比較。
static void Main(string[] args)
{//從largeW.txt中讀取數據//用 HashSet 的不可重復性去除重復HashSet<string> h = new HashSet<string>(File.ReadAllLines("largeW.txt"));string[] whiteList = new string[h.Count];
h.CopyTo(whiteList);int[] WhiteList = new int[whiteList.Length];for (int i = 0; i < whiteList.Length; ++i)
{
WhiteList[i] = int.Parse(whiteList[i]);
}
Array.Sort<int>(WhiteList);
Console.WriteLine("Type the numbers you want to query: ");//輸入樣例:5 824524 478510 387221string input = Console.ReadLine();int[] Query = new int[input.Split(' ').Length];for (int i = 0; i < Query.Length; ++i)
{
Query[i] = int.Parse(input.Split(' ')[i]);
}
Console.WriteLine("Irrelevant:");foreach (int n in Query)
{if (rank(n, WhiteList) == -1)
{
Console.WriteLine(n);
}
}
}//重載方法,用于啟動二分查找public static int rank(int key, int[] a)
{return rank(key, a, 0, a.Length - 1);
}//二分查找public static int rank(int key, int[] a, int lo, int hi)
{if (lo > hi)
{return -1;
}int mid = lo + (hi - lo) / 2;if (key < a[mid])
{return rank(key, a, lo, mid - 1);
}else if (key > a[mid])
{return rank(key, a, mid + 1, hi);
}else{return mid;
}
}等值鍵。
為 BinarySearch 類添加一個靜態方法 rank(),
它接受一個鍵和一個整型有序數組(可能存在重復值)作為參數
并返回數組中小于該鍵的元素數量,
以及一個類似的方法 count() 來返回數組中等于該鍵的元素數量。
注意:
如果 i 和 j 分別是 rank(key, a) 和 count(key, a) 的返回值,
那么 a[i..i + j - 1] 就是數組中所有和 key 相等的元素。
查找小于指定值的元素數量可以多次使用二分查找實現。
例如:
序號:0 1 2 3 4 5 6 7 8
元素:1 2 2 2 2 2 2 2 3
二分查找返回 4
再次在 0~3 之間查找
二分查找返回 1
再次在 0~1 之間查找
二分查找返回 -1,沒有指定值了
因此小于該值的元素數量就是 1 – 0 = 1 個
用同樣的方法可以找到大于指定值的元素個數,從總數中減去這兩個數值就是等于指定值的元素數量。
static void Main(string[] args)
{int[] WhiteList = new int[] { 1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6 };
Array.Sort<int>(WhiteList);
Console.WriteLine("Type the numbers you want to query: ");string input = Console.ReadLine();int[] Query = new int[input.Split(' ').Length];for (int i = 0; i < Query.Length; ++i)
{
Query[i] = int.Parse(input.Split(' ')[i]);
}
Console.WriteLine("Result:");foreach (int n in Query)
{int less = rank(n, WhiteList);int equal = count(n, WhiteList);
Console.WriteLine($"Less: {less} Equal: {equal}");
}
}//返回數組中相等元素的個數public static int count(int key, int[] a)
{int lowerBound = rank(key, a);int upperBound = lowerBound;if (lowerBound == -1)return 0;int result = 0;while (true)
{
result = rank(key, a, upperBound + 1, a.Length - 1);if (result == -1)break;if (result > upperBound)
{
upperBound = result;
}
}return upperBound - lowerBound + 1;
}//返回數組中小于該數的數字個數public static int rank(int key, int[] a)
{int mid = rank(key, a, 0, a.Length - 1);if (mid == -1)return 0;int result = mid;while (true)
{
result = rank(key, a, 0, mid - 1);if (result == -1)break;if (result < mid)
mid = result;
}return mid;
}//二分查找public static int rank(int key, int[] a, int lo, int hi)
{if (lo > hi)
{return -1;
}int mid = lo + (hi - lo) / 2;if (key < a[mid])
{return rank(key, a, lo, mid - 1);
}else if (key > a[mid])
{return rank(key, a, mid + 1, hi);
}else{return mid;
}
}
}數組練習。
編寫一段程序,創建一個 N×N 的布爾數組 a[][]。
其中當 i 和 j 互質時(沒有相同的因子),a[i][j] 為 true,否則為 false。
互質可以用之前的 GCD 最大公因數算法判斷,如果最大公因數是 1 則兩數互質。
//互質 = 最大公約數為 1 = gcd(i, j) == 1static void Main(string[] args)
{int N = int.Parse(Console.ReadLine());bool[,] a = new bool[N, N];for (int i = 0; i < N; ++i)
{for (int j = 0; j < N; ++j)
{
a[i, j] = (gcd(i, j) == 1);
}
}
PrintArray2D(a, N, N);
}static int gcd(int a, int b)
{if (b == 0)return a;return gcd(b, a % b);
}private static void PrintArray2D(bool[,] array, int rows, int columns)
{for (int i = 0; i < rows; i++)
{for (int j = 0; j < columns; j++)
{
Console.Write($"\t{array[i, j]}");
}
Console.Write("\n");
}
}
}隨機連接。
編寫一段程序,從命令行接受一個整數 N 和 double 值 p (0 到 1 之間)作為參數,
在一個圓上畫出大小為 0.05 且間距相等的 N 個點,
然后將每對點按照概率 p 用灰線連接。
概率的實現方法:
例如概率是 60 %,就在 [0, 100) 之間隨機一個值,小于等于 60 則執行操作,反之不執行。
需要更精確的情況可以增大隨機的范圍,例如 [0, 1000)。
繪圖結果:
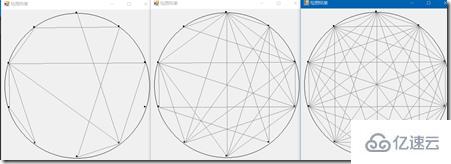
N = 10,p = 0.2, 0.5, 1
完整項目可以到 Github 上下載。
/// <summary>/// 主繪圖函數/// </summary>/// <param name="N">點的總數目</param>/// <param name="p">每對點之間連接的概率</param>public static void StartDrawing(int N, double p)
{int pointSize = 5;//每個點繪制的大小int precious = 1000;//概率判斷的精度//新建一個繪圖窗口Form2 DrawPad = new Form2();//顯示繪圖窗口 DrawPad.Show();//新建畫布Graphics graphics = DrawPad.CreateGraphics();//建立繪圖區域(矩形)Rectangle rect = new Rectangle(10, 10, 400, 400); //畫圓 graphics.DrawEllipse(Pens.Black, rect);//計算旋轉角度double rotateDgree = 360.0 / N;//計算點的坐標Point Center = new Point(rect.Top + rect.Height / 2, rect.Top + rect.Height / 2);
Point[] points = new Point[N];
points[0].X = rect.Left + rect.Width / 2;
points[0].Y = rect.Top;for (int i = 1; i < N; ++i)
{
points[i] = Rotate(Center, points[i - 1], rotateDgree);
}//繪制點foreach (Point point in points)
{
graphics.FillEllipse(Brushes.Black, point.X - pointSize, point.Y - pointSize, pointSize, pointSize);
}//按照概率繪制直線Random random = new Random();for (int i = 0; i < N; ++i)
{for (int j = i + 1; j < N; ++j)
{//舉例:輸入概率為 0.6,精度為 1000//在 0~1000 范圍內等概率取值,如果小于等于 600 則視為事件發生if (random.Next(0, precious) <= p * precious)
{
graphics.DrawLine(Pens.Gray, points[i], points[j]);
}
}
}//釋放資源 graphics.Dispose();
}/// <summary>/// 計算一個點繞某點旋轉之后的坐標值/// </summary>/// <param name="origin">旋轉的圓心</param>/// <param name="point">需要旋轉的點</param>/// <param name="dgree">旋轉的角度(逆時針)</param>/// <returns>返回旋轉后的坐標</returns>public static Point Rotate(Point origin, Point point, double dgree)
{
Point rotated = new Point();double dgreePi = dgree / 180 * Math.PI;
rotated.X = (int)((point.X - origin.X) * Math.Cos(dgreePi) -(point.Y - origin.Y) * Math.Sin(dgreePi) + origin.X);
rotated.Y = (int)((point.X - origin.X) * Math.Sin(dgreePi) +(point.Y - origin.Y) * Math.Cos(dgreePi) + origin.Y);return rotated;
}直方圖。
假設標準輸入流中含有一系列 double 值。
編寫一段程序,從命令行接受一個整數 N 和兩個 double 值 l 和 r。
將 (l, r) 分為 N 段并使用 StdDraw 畫出輸入流中的值落入每段的數量的直方圖。
繪圖結果:
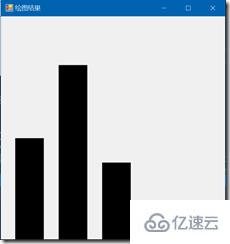
完整的項目代碼可以去 Github 上下載。
public static void StartDrawing(double[] array, int N, double l, double r)
{//創建并顯示繪圖窗口Form2 DrawPad = new Form2();
DrawPad.Show();//新建畫布Graphics graphics = DrawPad.CreateGraphics(); //翻轉默認坐標系graphics.TranslateTransform(0, DrawPad.Height);
graphics.ScaleTransform(1, -1);//對原始數組排序 Array.Sort(array);//計算各區域的值int[] counts = new int[N];int index = 0;for (int i = 0; i < N; ++i)
{for (int j = index; j < array.Length; ++j)
{if (array[j] <= (r - l) * (i + 1) / N)
{
counts[i]++;
index++;
}else{break;
}
}
}//獲取最大值double max = counts.Max();//計算間距double unit = DrawPad.Width / (3.0 * N + 1);//計算直方圖的矩形Rectangle[] rects = new Rectangle[N];
rects[0].X = (int)unit;
rects[0].Y = 0;
rects[0].Width = (int)(2 * unit);
rects[0].Height = (int)((counts[0] / max) * DrawPad.Height);for (int i = 1; i < N; ++i)
{
rects[i].X = (int)(rects[i - 1].X + 3 * unit);
rects[i].Y = 0;
rects[i].Width = (int)(2 * unit);
rects[i].Height = (int)((counts[i] / (max + 1)) * DrawPad.Height);
}//繪圖 graphics.FillRectangles(Brushes.Black, rects);//釋放資源 graphics.Dispose();
}矩陣庫。
編寫一個 Matrix 庫并實現以下 API
public class Matrix | 功能 |
static double dot(double[] x, double[] y) | 實現向量點乘 |
static double[][] mult(double[][] a, double[][] b) | 矩陣與矩陣相乘 |
static double[][] transpose(double[][] a) | 矩陣轉置 |
static double[] mult(double[][] a, double[] x) | 矩陣與向量相乘 |
static double[] mult(double[] y, double[][] a) | 向量與矩陣相乘 |
編寫一個測試用例,從標準輸入讀取矩陣并測試所有方法。
這里矩陣使用交錯數組實現(方便取行向量),不是普通的二維數組。
矩陣和矩陣、矩陣和向量、向量和矩陣都使用行向量點乘列向量的方式計算。
public class Matrix
{/// <summary>/// 計算兩個向量的點積/// </summary>/// <param name="x">需要點乘的向量</param>/// <param name="y">需要點乘的另一個向量</param>/// <returns>返回點乘的結果</returns>/// <exception cref="FormatException"></exception>public static double Dot(double[] x, double[] y)
{//確保兩向量等長if (x.Length != y.Length)
{throw new FormatException("the length of two vectors must be equal");
}//點乘double result = 0;for (int i = 0; i < x.Length; ++i)
{
result += x[i] * y[i];
}return result;
}/// <summary>/// 計算兩個矩陣相乘的結果,返回一個矩陣/// </summary>/// <param name="a">用交錯數組表示的 m * p 矩陣</param>/// <param name="b">用交錯數組表示的 p * n 矩陣</param>/// <returns>返回 m * n 的矩陣</returns>/// <exception cref="FormatException"></exception>/// <example>/// a = {(1,2,3),(4,5,6)}/// b = {(1,4),(2,5),(3,6)}/// Mult(a, b) = {(14,32),(32,77)}/// </example>public static double[][] Mult(double[][] a, double[][] b)
{if (a[0].Length != b.GetLength(0))
{throw new FormatException("a's column number must be equal to b's row number");
}int m = a.GetLength(0);int n = b[0].Length;int p = a[0].Length;double[][] result = new double[m][];for (int i = 0; i < m; ++i)
{double[] resultrow = new double[n];for (int j = 0; j < n; ++j)
{//result[i][j] = 行向量 a[i] 與列向量 b[j] 的點積double[] row = a[i];double[] col = new double[p];//取得列向量for (int k = 0; k < p; ++k)
{
col[k] = b[k][j];
}//點積resultrow[j] = Dot(row, col);
}
result[i] = resultrow;
}return result;
}/// <summary>/// 將一個矩陣轉置/// </summary>/// <param name="a">待轉置的矩陣</param>/// <returns>返回轉置后的數組</returns>public static double[][] Transpose(double[][] a)
{double[][] trans = new double[a[0].Length][];for (int i = 0; i < a[0].Length; ++i)
{double[] row = new double[a.GetLength(0)];for (int j = 0; j < a.GetLength(0); ++j)
{
row[j] = a[j][i];
}
trans[i] = row;
}return trans;
}/// <summary>/// 計算矩陣與向量的乘積/// </summary>/// <param name="a">左乘的矩陣</param>/// <param name="x">列向量</param>/// <returns>返回一個向量</returns>/// <exception cref="FormatException"></exception>public static double[] Mult(double[][] a, double[] x)
{if (a[0].Length != x.Length)
{throw new FormatException("a's column number must be equal to x's length");
}double[] result = new double[a.GetLength(0)];for (int i = 0; i < a.GetLength(0); ++i)
{
result[i] = Dot(a[i], x);
}return result;
}/// <summary>/// 計算向量與矩陣的乘積/// </summary>/// <param name="x">行向量</param>/// <param name="a">矩陣</param>/// <returns>返回一個向量</returns>/// <exception cref="FormatException"></exception>public static double[] Mult(double[] x, double[][] a)
{if (a.GetLength(0) != x.Length)
{throw new FormatException("a's column number must be equal to x's length");
}double[] result = new double[a[0].Length];for (int i = 0; i < a[0].Length; ++i)
{double[] colVector = new double[a.GetLength(0)];for (int j = 0; j < colVector.Length; ++j)
{
colVector[j] = a[j][i];
}
result[i] = Dot(x, colVector);
}return result;
}/// <summary>/// 在控制臺上輸出矩陣/// </summary>/// <param name="a">需要輸出的矩陣</param>public static void PrintMatrix(double[][] a)
{for (int i = 0; i < a.GetLength(0); ++i)
{for (int j = 0; j < a[i].Length; ++j)
{
Console.Write($"\t{a[i][j]}");
}
Console.Write("\n");
}
}/// <summary>/// 在控制臺上輸出一行向量/// </summary>/// <param name="a">需要輸出的向量</param>public static void PrintVector(double[] a)
{for (int i = 0; i < a.Length; ++i)
{
Console.Write($"\t{a[i]}");
}
Console.Write("\n");
}
}過濾。
以下那些任務需要(在數組中,比如)保存標準輸入中的所有值?
那些可以被實現為一個過濾器且僅使用固定數量的變量和固定大小的數組(和 N 無關)?
每個問題中,輸入都是來自于標準輸入且含有 N 個 0 到 1 的實數。
打印出最大和最小的數
打印出所有數的中位數
打印出第 k 小的數, k 小于 100
打印出所有數的平方和
打印出 N 個數的平均值
打印出大于平均值的數的百分比
將 N 個數按照升序打印
將 N 個數按照隨機順序打印
第二個以及最后三個需要,其他都可以設計成過濾器的模式。
這里的 largeW.txt 只需要保留前 100 個數字就可以了,太多的話最后兩個測試會刷屏。
static void Main(string[] args)
{string[] AllNumbers = File.ReadAllLines("largeW.txt");int N = AllNumbers.Length;int[] input = new int[N];for (int i = 0; i < N; ++i)
{
input[i] = int.Parse(AllNumbers[i]);
}
MinAndMax(input);
Console.WriteLine();
MidNumber(input);
Console.WriteLine();
NumberK(4, input);
Console.WriteLine();
SquareSum(input);
Console.WriteLine();
AboveAverage(input);
Console.WriteLine();
Ascending(input);
Console.WriteLine();
Shuffle(input);
Console.WriteLine();
}/// <summary>/// 獲取最大值和最小值/// </summary>/// <param name="input">輸入流</param>static void MinAndMax(int[] input)
{//只用到了兩個變量int min = input[0];int max = input[0];//只對輸入值正向遍歷一遍,不需要保存for (int i = 1; i < input.Length; ++i)
{if (input[i] > max)
{
max = input[i];
}if (input[i] < min)
{
min = input[i];
}
}
Console.WriteLine("Min and Max:");
Console.WriteLine($"Min: {min}\nMax: {max}");
}/// <summary>/// 獲取中位數/// </summary>/// <param name="input">輸入流</param>/// <returns>中位數</returns>static int MidNumber(int[] input)
{//需要對輸入值進行去重 & 排序,故需要保存List<int> DistinctNumbers = new List<int>(input.Distinct());
DistinctNumbers.Sort();
Console.WriteLine("MidNumber:");
Console.WriteLine(DistinctNumbers[DistinctNumbers.Count / 2]);return DistinctNumbers[DistinctNumbers.Count / 2];
}/// <summary>/// 獲取第 k 小的數/// </summary>/// <param name="k">需要獲取的排名</param>/// <param name="input">輸入流</param>/// <returns>第 k 小的數</returns>static int NumberK (int k, int[] input)
{int[] temp = new int[101];//只正向遍歷一遍,不需要保存for (int i = 0; i < input.Length; ++i)
{if (i < 100)
{
temp[i] = input[i];
}else{
temp[100] = input[i];
Array.Sort(temp);
}
}
Console.WriteLine("NumberK");
Console.WriteLine($"No.k: {temp[k - 1]}");return temp[k - 1];
}/// <summary>/// 計算輸入流中所有數的平方和/// </summary>/// <param name="input">輸入流</param>/// <returns>所有數的平方和</returns>static long SquareSum(int[] input)
{long sum = 0;//只正向遍歷一遍,不需要保存for (int i = 0; i < input.Length; ++i)
{
sum += input[i] * input[i];
}
Console.WriteLine("Sum Of Square:");
Console.WriteLine(sum);return sum;
}/// <summary>/// 計算所有輸入數據的平均值/// </summary>/// <param name="input">輸入流</param>/// <returns>所有輸入數據的平均值</returns>static double Average(int[] input)
{long sum = 0;//只遍歷一遍,且不保存整個數組for (int i = 0; i < input.Length; ++i)
{
sum += input[i];
}double ave = sum / (double)input.Length;
Console.WriteLine("Average:");
Console.WriteLine(ave);return ave;
}/// <summary>/// 計算大于平均值的元素數量/// </summary>/// <param name="input">輸入流</param>/// <returns>大于平均值的元素數量</returns>static double AboveAverage(int[] input)
{double ave = Average(input);
Console.WriteLine();double count = 0;for (int i = 0; i < input.Length; ++i)
{if (input[i] > ave)
{
count++;
}
}
Console.WriteLine("AboveAverage:");
Console.WriteLine($"{(count / input.Length) * 100}%");return count;
}/// <summary>/// 升序打印數組/// </summary>/// <param name="input">輸入流</param>static void Ascending(int[] input)
{
Array.Sort(input);
Console.WriteLine("Ascending:");for (int i = 0; i < input.Length; ++i)
{
Console.Write($" {input[i]}");
}
Console.Write("\n");
}/// <summary>/// 隨機打印數組/// </summary>/// <param name="input">輸入流</param>static void Shuffle(int[] input)
{
Random random = new Random();
List<int> All = new List<int>(input);int N = input.Length;int temp = 0;
Console.WriteLine("Shuffle:");for (int i = 0; i < N; ++i)
{
temp = random.Next(0, All.Count - 1);
Console.Write($" {All[temp]}");
All.RemoveAt(temp);
}
}模擬擲骰子。
以下代碼能夠計算每種兩個骰子之和的準確概率分布:
int SIDE = 6;double[] dist = new double[2 * SIDES + 1];for (int I = 1; i <= SIDES; i++)for (int j = 1; j <= SIDES; j++) dist[i + j] += 1.0;for (int k = 2; k <= 2 * SIDES; k++) dist[k] /= 36.0;
dist[i] 的值就是兩個骰子之和為 i 的概率。
用實驗模擬 N 次擲骰子,
并在計算兩個 1 到 6 之間的隨機整數之和時記錄每個值出現頻率以驗證它們的概率。
N 要多大才能夠保證你的經驗數據和準確數據的吻合程度達到小數點后 3 位?
這里用 Random 類模擬擲骰子并計算概率,最后和程序得出的比較。
//程序運行大概需要十幾秒時間(也可能更長,看運氣)//我的數據://24098 44448 37776 44401 32541static void Main(string[] args)
{//書中給出的程序int SIDES = 6;double[] dist = new double[2 * SIDES + 1];for (int i = 1; i <= SIDES; i++)for (int j = 1; j <= SIDES; j++)
dist[i + j] += 1.0;for (int k = 2; k <= 2 * SIDES; k++)
dist[k] /= 36.0;//不斷進行模擬,直至誤差小于 0.001int N = 36;bool isAccepted = false;double[] disttemp = null;double error = 0.001;while (isAccepted == false)
{
disttemp = PlayDice(N);
isAccepted = true;for (int i = 0; i < disttemp.Length; ++i)
{if (Math.Abs(disttemp[i] - dist[i]) >= error)
isAccepted = false;
}
N++;
}
Console.WriteLine($"N:{N}\n");for (int i = 0; i < dist.Length; ++i)
{
Console.WriteLine($"{i}:\n Standerd:{dist[i]}\nSimulated:{disttemp[i]}\nOffset:{Math.Abs(disttemp[i] - dist[i])}");
}
}//利用隨機數模擬擲骰子static double[] PlayDice(int N)
{
Random random = new Random();int SIDES = 6;double[] dist = new double[2 * SIDES + 1];//擲 N 次int sumtemp = 0;for (int i = 0; i < N; ++i)
{
sumtemp = random.Next(1, 7) + random.Next(1, 7);
dist[sumtemp]++;
}//計算概率for (int i = 0; i < dist.Length; ++i)
{
dist[i] /= N;
}return dist;
}亂序檢查。
通過實驗檢查表 1.1.10 中的亂序代碼是否能夠產生預期的效果。
編寫一個程序 ShuttleTest,接受命令行參數 M 和 N,
將大小為 M 的數組打亂 N 次且在每次打亂之前都將數組重新初始化為 a[i] = i。
打印一個 M×M 的表格,對于所有的列 j,行 i 表示的是 i 在打亂后落到 j 的位置的次數。
數組中的所有元素的值都應該接近于 N/M。
N 取到 1000 左右數據就比較明顯了。
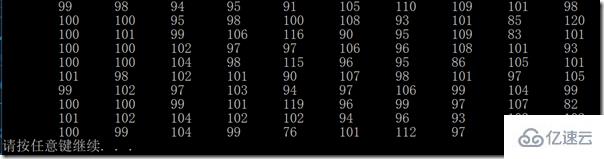
N = 1000, M = 10
static void Main(string[] args)
{int M = 10;//數組大小int N = 1000;//打亂次數int[] a = new int[10];int[,] result = new int[M, M];for (int i = 0; i < N; ++i)
{//初始化for (int j = 0; j < a.Length; ++j)
{
a[j] = j;
}//打亂 Shuffle(a, i);//記錄for (int j = 0; j < M; ++j)
{
result[a[j], j]++;
}
}
PrintMatrix(result);
}/// <summary>/// 打亂數組/// </summary>/// <param name="a">需要打亂的數組</param>/// <param name="seed">用于生成隨機數的種子值</param>static void Shuffle(int[] a, int seed)
{int N = a.Length;
Random random = new Random(seed);for (int i = 0; i < N; ++i)
{int r = i + random.Next(N - i);//等于StdRandom.uniform(N-i)int temp = a[i];
a[i] = a[r];
a[r] = temp;
}
}/// <summary>/// 在控制臺上輸出矩陣/// </summary>/// <param name="a">需要輸出的矩陣</param>public static void PrintMatrix(int[,] a)
{for (int i = 0; i < a.GetLength(0); ++i)
{for (int j = 0; j < a.GetLength(1); ++j)
{
Console.Write($"\t{a[i,j]}");
}
Console.Write("\n");
}
}糟糕的打亂。
假設在我們的亂序代碼中你選擇的是一個 0 到 N - 1 而非 i 到 N - 1 之間的隨機整數。
證明得到的結果并非均勻地分布在 N! 種可能性之間。
用上一題中的測試檢驗這個版本。
使用 0~N-1 的隨機數會導致每次交換的數字可能相同。
例如:
原數組: 1 2 3 4。
第一次: 2 1 3 4 random = 1,第 0 個和第 1 個交換。
第二次: 1 2 3 4 random = 0,第 1 個和第 0 個交換。
static void Main(string[] args)
{int M = 10;//數組大小int N = 100000;//打亂次數int[] a = new int[10];int[,] result = new int[M, M];for (int i = 0; i < N; ++i)
{//初始化for (int j = 0; j < a.Length; ++j)
{
a[j] = j;
}//打亂 Shuffle(a, i);//記錄for (int j = 0; j < M; ++j)
{
result[a[j], j]++;
}
}
PrintMatrix(result);
}/// <summary>/// 打亂數組(不夠好的版本)/// </summary>/// <param name="a">需要打亂的數組</param>/// <param name="seed">用于生成隨機數的種子值</param>static void Shuffle(int[] a, int seed)
{int N = a.Length;
Random random = new Random(seed);for (int i = 0; i < N; ++i)
{//int r = i + random.Next(N - i);int r = random.Next(N); //返回的是 0 ~ N-1 之間的隨機整數int temp = a[i];
a[i] = a[r];
a[r] = temp;
}
}/// <summary>/// 在控制臺上輸出矩陣/// </summary>/// <param name="a">需要輸出的矩陣</param>public static void PrintMatrix(int[,] a)
{for (int i = 0; i < a.GetLength(0); ++i)
{for (int j = 0; j < a.GetLength(1); ++j)
{
Console.Write($"\t{a[i, j]}");
}
Console.Write("\n");
}
}二分查找與暴力查找。
根據 1.1.10.4 節給出的暴力查找法編寫一個程序 BruteForceSearch,
在你的計算機上比較它和 BinarySearch 處理 largeW.txt 和 largeT.txt 所需的時間。
為了使差距比較明顯,故意取了比較靠后的數字。
static void Main(string[] args)
{string[] largeWString = File.ReadAllLines("largeW.txt");int[] largeW = new int[largeWString.Length];for (int i = 0; i < largeW.Length; ++i)
{
largeW[i] = int.Parse(largeWString[i]);
}
Stopwatch timer = Stopwatch.StartNew();
BruteForceSearch(111111, largeW);
Console.WriteLine($"BruteForceSearch: {timer.ElapsedMilliseconds} ms");
timer.Restart();
rank(111111, largeW);
Console.WriteLine($"BinarySearch: {timer.ElapsedMilliseconds} ms");string[] largeTString = File.ReadAllLines("largeT.txt");int[] largeT = new int[largeTString.Length];for (int i = 0; i < largeW.Length; ++i)
{
largeT[i] = int.Parse(largeTString[i]);
}
timer.Restart();
BruteForceSearch(111111, largeT);
Console.WriteLine($"BruteForceSearch: {timer.ElapsedMilliseconds} ms");
timer.Restart();
rank(111111, largeT);
Console.WriteLine($"BinarySearch: {timer.ElapsedMilliseconds} ms");
}//暴力查找public static int BruteForceSearch(int key, int[] a)
{for (int i = 0; i < a.Length; ++i)
{if (a[i] == key)return i;
}return -1;
}//重載方法,用于啟動二分查找public static int rank(int key, int[] a)
{return rank(key, a, 0, a.Length - 1, 1);
}//二分查找public static int rank(int key, int[] a, int lo, int hi, int number)
{if (lo > hi)
{return -1;
}int mid = lo + (hi - lo) / 2;if (key < a[mid])
{return rank(key, a, lo, mid - 1, number + 1);
}else if (key > a[mid])
{return rank(key, a, mid + 1, hi, number + 1);
}else{return mid;
}
}隨機匹配。
編寫一個使用 BinarySearch 的程序,
它從命令行接受一個整型參數 T,
并會分別針對 N = 10^3、10^4、10^5 和 10^6 將以下實驗運行 T 遍:
生成兩個大小為 N 的隨機 6 位正整數數組并找出同時存在于兩個數組中的整數的數量。
打印一個表格,對于每個 N,給出 T 次實驗中該數量的平均值。
按照要求編程就好,視機器不同需要的時間也不同。
//需要 6 秒左右的運算時間static void Main(string[] args)
{
Random r = new Random();int baseNum = 10;int powNum = 3;int T = 10;int M = 4;double[,] Matrix = new double[M,2];for (int i = 0; i < M; ++i)
{int N = (int)Math.Pow(baseNum, powNum + i);double sum = 0;for (int j = 0; j < T; ++j)
{
sum += Test(N, r.Next());
}
Matrix[i, 0] = N;
Matrix[i, 1] = sum / T;
}
PrintMatrix(Matrix);
}/// <summary>/// 執行一次“實驗”/// </summary>/// <param name="N">數組的大小</param>/// <param name="seed">隨機種子</param>/// <returns>返回相同數字的數目</returns>static int Test(int N, int seed)
{
Random random = new Random(seed);int[] a = new int[N];int[] b = new int[N];int count = 0;for (int i = 0; i < N; ++i)
{
a[i] = random.Next(100000, 1000000);
b[i] = random.Next(100000, 1000000);
}for (int i = 0; i < N; ++i)
{if (rank(a[i], b) != -1)
count++;
}return count;
}//重載方法,用于啟動二分查找public static int rank(int key, int[] a)
{return rank(key, a, 0, a.Length - 1, 1);
}//二分查找public static int rank(int key, int[] a, int lo, int hi, int number)
{if (lo > hi)
{return -1;
}int mid = lo + (hi - lo) / 2;if (key < a[mid])
{return rank(key, a, lo, mid - 1, number + 1);
}else if (key > a[mid])
{return rank(key, a, mid + 1, hi, number + 1);
}else{return mid;
}
}/// <summary>/// 在控制臺上輸出矩陣/// </summary>/// <param name="a">需要輸出的矩陣</param>public static void PrintMatrix(double[,] a)
{for (int i = 0; i < a.GetLength(0); ++i)
{for (int j = 0; j < a.GetLength(1); ++j)
{
Console.Write($"\t{a[i, j]}");
}
Console.Write("\n");
}
}感謝你能夠認真閱讀完這篇文章,希望小編分享的“C#中算法的實例詳解”這篇文章對大家有幫助,同時也希望大家多多支持億速云,關注億速云行業資訊頻道,更多相關知識等著你來學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。