您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
如何用dijkstra算法找到五一最省旅游路線?這個問題可能是我們日常學習或工作經常見到的。希望通過這個問題能讓你收獲頗深。下面是小編給大家帶來的參考內容,讓我們一起來看看吧!
案例:
查了查到各地的機票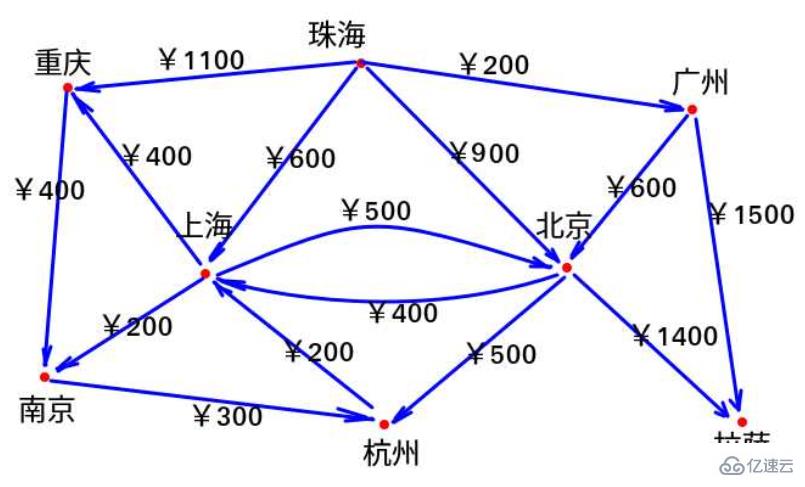
因為今年被扣工資扣得很慘,小張手頭不是很寬裕,必須精打細算。他想弄清去各個城市的最低開銷。
【嗯,不用考慮回來的開銷。小張準備找警察叔叔說自己被拐賣,免費被送回來。】
如果他想從珠海飛到拉薩,最少要花多少機票錢呢?下面就說到我們今天要說的這個算法。
Dijkstra(迪杰斯特拉)算法是典型的單源最短路徑算法,用于計算一個節點到其他所有節點的最短路徑。主要特點是以起始點為中心向外層層擴展,直到擴展到終點為止。Dijkstra算法的時間復雜度為O(N^2)。
狄克斯特拉Dijkstra1930年5月11日生于荷蘭鹿特丹的一個知識分子家庭,在兄弟姊妹4人中排行第三。他的父親是一名化學家和發明家,曾擔任荷蘭化學會主席。他母親則是一位數學家。他成功地設計并實現了在有障礙物的兩個地點之間找出一條最短路徑的高效算法,這個算法被命名為“狄克斯特拉算法”,解決了機器人學中的一個十分關鍵的問題,即運動路徑規劃問題,至今仍被廣泛應用。
相關教程:數據結構探險之圖篇
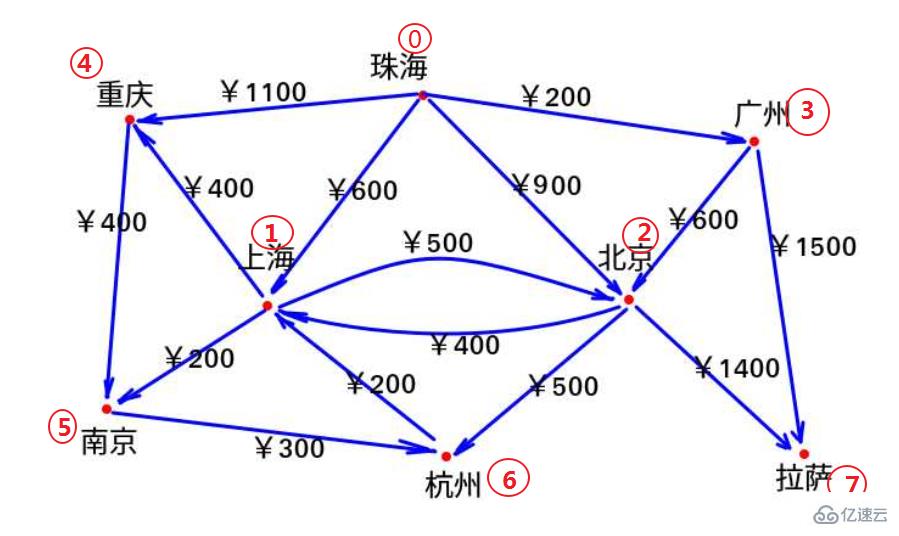
珠海直達的城市有上海、北京、廣州、重慶,那么珠海到其他城市的機票價格如下(無法直達的我們標記無窮大):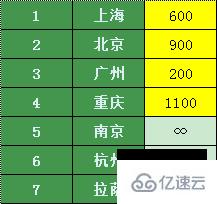
可以看出,這4個城市中廣州價格最低,那我們就從廣州轉機吧
廣州能直達的城市有北京、拉薩,那么珠海從廣州轉機到達其他城市的機票價格如下:(無法知道就能從廣州轉機)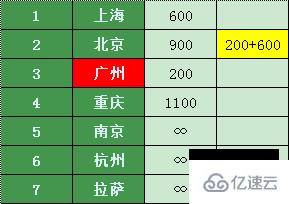
對比發現從珠海到廣州 200 ,廣州到北京600,算下來才800塊錢(可能時間花銷上損失,管他呢,小張窮的只剩下時間了)
從廣州中轉,到拉薩1700,那么肯定比到不了強。
這么算下來我們有最便宜的價格表了。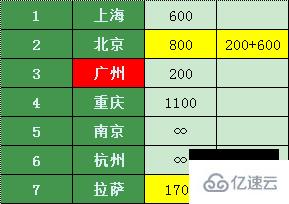
上海直達的城市重慶、南京,那么珠海從上海轉機到達其他城市的機票價格如下: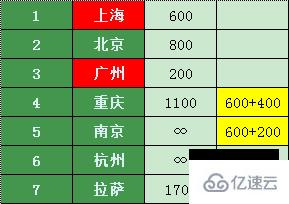
對比原來的價格,發現上海中轉到重慶、南京比較便宜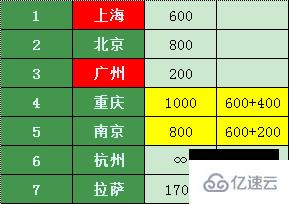
北京直達上海(上海已經被標記了,肯定已經是最便宜的價格,其實已經沒有比較的意義)、杭州和拉薩,價格如下:
到拉薩的價格 即 到北京最低的價格800 + 北京 -> 拉薩 1400 的價格之和(2200)高于1700,到杭州 800 + 500 = 1300,那么最低價格表如下
南京只能直達杭州,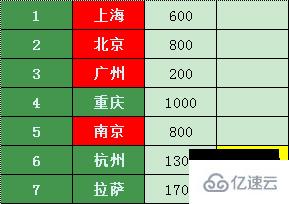
南京到杭州的價格為1100,劃算
重慶直達的只有南京,且到南京需要1000 + 400 = 1400元,和原來的到南京的800比,肯定不合算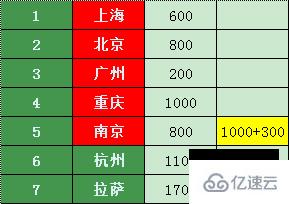
杭州也只能到上海,且比上海價格高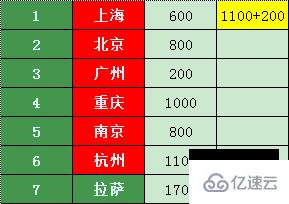

那么拉薩最便宜的機票就是1700元。
1)用0,1,2,. . . ,7分別表示珠海,上海,北京,廣州,重慶,南京,杭州,拉薩。
2)用一個二維數組 prices [8][8] 來表示航班價格:prices[i][j] = i到j的直飛價格(如無航班記作∞)
3)用一個數組minPrice來記錄珠海到各個城市的最少機票開銷:
4)用一個數組flag標記城市是否已經轉機過
// 表示無窮大 即不可達
public static int NO_AIRPLANE = Integer.MAX_VALUE;
// 初始直飛價格表
public int[][] prices ;
// 最優轉機價格表
public int[] minPrice ;
public boolean[] flag ;
private int citySize; public static int[][] getPrices(){
int ZH = 0,SH = 1, BJ = 2, GZ = 3,CQ = 4,NJ = 5, HZ = 6,LS = 7;
int[][] prices = new int[8][8];
//from Zhuhai
prices[ZH][CQ] = 1100;
prices[ZH][SH] = 600;
prices[ZH][BJ] = 900;
prices[ZH][GZ] = 200;
//others
prices[CQ][NJ] = 400;
prices[SH][CQ] = 400;
prices[SH][BJ] = 500;
prices[SH][NJ] = 200;
prices[BJ][SH] = 400;
prices[BJ][HZ] = 500 ;
prices[BJ][LS] = 1400;
prices[GZ][BJ] = 600 ;
prices[GZ][LS] = 1500 ;
prices[NJ][HZ] = 300 ;
prices[HZ][SH] = 200 ;
for(int i = 0 ; i < 8 ; i++){
for(int j = 0 ; j < 8 ; j++){
if(prices[i][j] == 0){
prices[i][j] = NO_AIRPLANE;
}
}
}
return prices;
}// 初始化始發站價格表
for(int i = 1; i < citySize;i++){
minPrice[i-1] = prices[0][i];
}private void dijkstra(){
int min = Integer.MAX_VALUE;
int minIdx = Integer.MAX_VALUE;
// 找到最小的價格
for(int idx = 0 ; idx < minPrice.length ; idx ++ ) {
if(!flag[idx] && minPrice[idx] < min ){
min = minPrice[idx];
minIdx = idx ;
}
}
if(minIdx == Integer.MAX_VALUE){
// 已經沒有最小的了
return ;
}
//標記從該城市轉機
flag[minIdx] = true;
minIdx += 1;
System.out.println("最小城市序號"+minIdx +" 價格"+ minPrice[minIdx -1]);
// 獲取當前城市的價格表
int cityPrice = minPrice[minIdx -1];
int[] minCityPrices = prices[minIdx];
for(int idx = 1 ; idx < citySize ; idx ++ ){
int price = minCityPrices[idx];
// 如果從杭州到達該城市的價格 加上 idx城市轉機的價格 低于 從杭州到達idx城市的價格 則更新
if(!flag[idx -1 ] && price != NO_AIRPLANE && (cityPrice+ price) < minPrice[idx - 1]){
// 可達的城市到達的
minPrice[idx - 1] = cityPrice+ price;
System.out.println(idx+"更新最優表:" + Arrays.toString(minPrice));
}
}
dijkstra();
}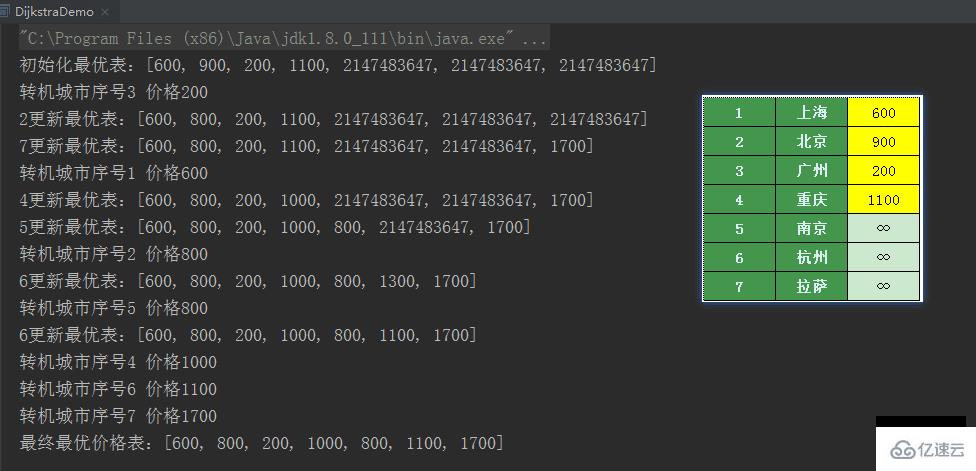
跟上述推到過程一致,希望本文能對你有所幫助。
附件-源碼:
package a;
import java.util.Arrays;
/**
* ┏┓ ┏┓+ +
* ┏┛┻━━━┛┻┓ + +
* ┃ ┃
* ┃ ━ ┃ ++ + + +
* ████━████ ┃+
* ┃ ┃ +
* ┃ ┻ ┃
* ┃ ┃ + +
* ┗━┓ ┏━┛
* ┃ ┃
* ┃ ┃ + + + +
* ┃ ┃ Code is far away from bug with the animal protecting
* ┃ ┃ + 神獸保佑,代碼無bug
* ┃ ┃
* ┃ ┃ +
* ┃ ┗━━━┓ + +
* ┃ ┣┓
* ┃ ┏┛
* ┗┓┓┏━┳┓┏┛ + + + +
* ┃┫┫ ┃┫┫
* ┗┻┛ ┗┻┛+ + + +
*
* @Author:Halburt
* @Date:2019-04-24 下午 5:47
* @Description:
*/
public class DijkstraDemo {
// 表示無窮大 即不可達
public static int NO_AIRPLANE = Integer.MAX_VALUE;
// 初始直飛價格表
public int[][] prices ;
// 最優轉機價格表
public int[] minPrice ;
public boolean[] flag ;
private int citySize;
/**
* @param citySize 城市數量
*/
public DijkstraDemo(int citySize){
this.citySize = citySize;
// prices = new int [citySize][citySize];
flag = new boolean [citySize - 1];
minPrice = new int[citySize - 1 ];
}
public static int[][] getPrices(){
int ZH = 0,SH = 1, BJ = 2, GZ = 3,CQ = 4,NJ = 5, HZ = 6,LS = 7;
int[][] prices = new int[8][8];
//from Zhuhai
prices[ZH][CQ] = 1100;
prices[ZH][SH] = 600;
prices[ZH][BJ] = 900;
prices[ZH][GZ] = 200;
//others
prices[CQ][NJ] = 400;
prices[SH][CQ] = 400;
prices[SH][BJ] = 500;
prices[SH][NJ] = 200;
prices[BJ][SH] = 400;
prices[BJ][HZ] = 500 ;
prices[BJ][LS] = 1400;
prices[GZ][BJ] = 600 ;
prices[GZ][LS] = 1500 ;
prices[NJ][HZ] = 300 ;
prices[HZ][SH] = 200 ;
for(int i = 0 ; i < 8 ; i++){
for(int j = 0 ; j < 8 ; j++){
if(prices[i][j] == 0){
prices[i][j] = NO_AIRPLANE;
}
}
}
return prices;
}
public static void main(String[] args) {
DijkstraDemo demo = new DijkstraDemo(8);
demo.dijkstra(getPrices());
}
public void dijkstra(int[][] prices ){
this.prices = prices;
// 初始化
// 初始化始發站價格表
for(int i = 1; i < citySize;i++){
minPrice[i-1] = prices[0][i];
}
System.out.println("初始化最優表:" + Arrays.toString(minPrice));
dijkstra();
System.out.println("最終最優價格表:" + Arrays.toString(minPrice));
}
private void dijkstra(){
int min = Integer.MAX_VALUE;
int minIdx = Integer.MAX_VALUE;
// 找到最小的價格
for(int idx = 0 ; idx < minPrice.length ; idx ++ ) {
if(!flag[idx] && minPrice[idx] < min ){
min = minPrice[idx];
minIdx = idx ;
}
}//=已經沒有最小的了
if(minIdx == Integer.MAX_VALUE){
return ;
}
//標記從該城市轉機
flag[minIdx] = true;
minIdx += 1;
System.out.println("轉機城市序號"+minIdx +" 價格"+ minPrice[minIdx -1]);
//獲取該城市轉機時飛往其他城市的價格表
int cityPrice = minPrice[minIdx -1];
//獲取杭州飛往該城市的價格
int[] minCityPrices = prices[minIdx];
for(int idx = 1 ; idx < citySize ; idx ++ ){
int price = minCityPrices[idx];
// 如果從杭州到達該城市的價格 加上 idx城市轉機的價格 低于 從杭州到達idx城市的價格 則更新
if(!flag[idx -1 ] && price != NO_AIRPLANE && (cityPrice+ price) < minPrice[idx - 1]){
// 可達的城市到達的
minPrice[idx - 1] = cityPrice+ price;
System.out.println(idx+"更新最優表:" + Arrays.toString(minPrice));
}
}
dijkstra();
}
}感謝各位的閱讀!看完上述內容,你們對如何用dijkstra算法找到五一最省旅游路線大概了解了嗎?希望文章內容對大家有所幫助。如果想了解更多相關文章內容,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。