Curves(曲線)

周一到周五，每天一篇，北京時間早上7點準時更新~

Curves(曲線)

If moving everything along a straight line between two points is all we wanted to do, then this would be enough. However, in the real world, objects move in smooth curves and accelerate and decelerate smoothly. A curve can be represented by three or more control points. For most curves, there are more than three control points, two of which form the endpoints; the others define the shape of the curve. Consider the simple curve shown in Figure 4.14

如果沿著一條直線運動就能滿足我們的所有需求，那么線性插值就足夠了，然而，實際上，物體更多的是沿著曲線運動，慢慢的加速和減速。三個或者三個以上的點可以表達一個曲線，大部分曲線有三個以上的控制點。 其中兩個點用來定義邊界，其他的點用來定義曲線的形狀，圖4.14展示了一個簡單的曲線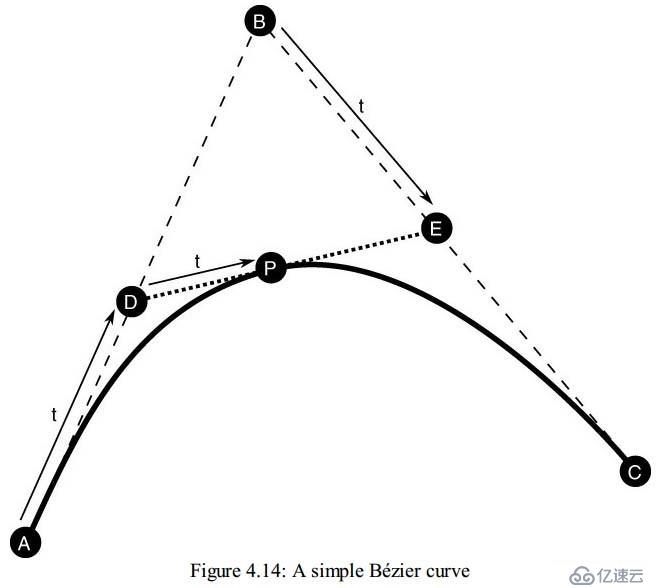

The curve shown in Figure 4.14 has three control points, A, B, and C. A and C are theendpoints of the curve and B defines the shape of the curve. If we join points A and B with one line and points B and C together with another line, then we can interpolate along the two lines using a simple linear interpolation to find a new pair of points, D and E. Now, given these two points, we can join them with yet another line and interpolate along it to find a new point, P. As we vary our interpolation parameter, t, point P will move in a smooth curved path from A to D. Expressed mathematically, this is

圖4.14中的曲線有3個控制點，其中A和C是端點，B控制著曲線的形狀。如果我們將AB和BC連起來，我們就可以沿著這兩條線段進行線性插值，找到類似于D、E這樣的一對一對的點。 連接D、E兩點又可以得到一條新的線段，插值這條線又會得到新的點p。當我們去讓t變化，就可以得到p點從A到D平滑運動，計算公式如下：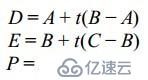

Substituting for D and E and doing a little crunching, we come up with the following:(同樣的對于D、E之間的插值，我們有如下式子:)

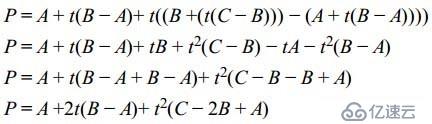
You should recognize this as a quadratic equation in t. The curve that it describes is known as a quadratic Bézier curve(你會發現，這個插值實際上就是二階的貝塞爾曲線). We can actually implement this very easily in GLSL using the mix function, as all we’re doing is linearly interpolating (mixing) the results of two previous interpolations(我們在GLSL里面很容易去實現這一插值)

vec4 quadratic_bezier(vec4 A, vec4 B, vec4 C, float t)
{
vec4 D = mix(A, B, t); // D = A + t(B - A)
vec4 E = mix(B, C, t); // E = B + t(C - B)
vec4 P = mix(D, E, t); // P = D + t(E - D)
return P;
}
By adding a fourth control point as shown in Figure 4.15, we can increase the order by 1 and produce a cubic Bézier curve.

當我們添加第四個控制點后，這個插值又變成了三次方的貝塞爾曲線了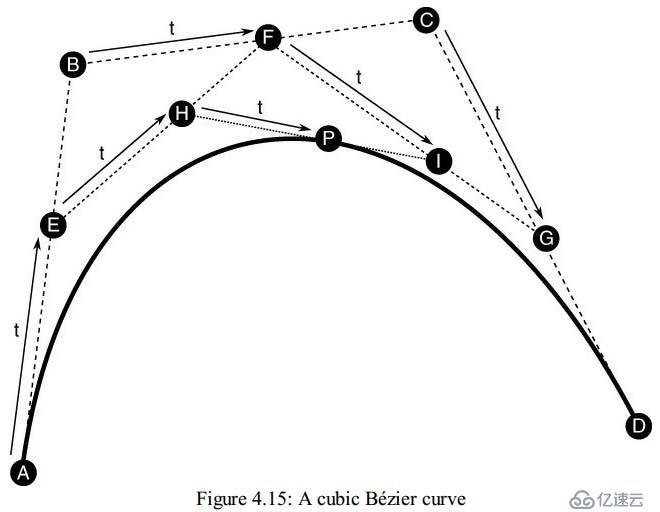

We now have four control points, A, B, C, and D. The process for constructing the curve is similar to that for the quadratic Bézier curve. We form a first line from A to B, a second line from B to C, and a third line from C to D. Interpolating along each of the three lines gives rise to three new points, E, F, and G. Using these three points, we form two more lines, one from E to F and another from F to G, interpolating along which gives rise to points H and I, between which we can interpolate to find our final point, P. Therefore, we have

現在我們有四個控制點了，構建曲線的方法跟三個控制點構建曲線的方法類似。我們首先連接AB、BC、CD，然后分別對他們插值，得到新的點E、F、G。然后用這仨點做出新的兩條線EF、FG， 然后繼續對EF、FG插值得到H、I點，然后我們對HI進行插值，得到了p點，這樣一來我們有下面的公式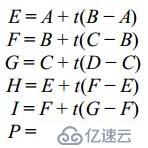

If you think these equations look familiar, you’re right: Our points E, F, and G form a quadratic Bézier curve that we use to interpolate to our final point P. If we were to substitute the equations for E, F, and G into the equations for H and I, then substitute those into the equation for P, and crunch through the expansions, we would be left with a cubic equation with terms in t—hence the name cubic Bézier curve. Again, we can implement this simply and efficiently in terms of linear interpolations in GLSL using the mix function:

如果你覺得這個等式非常相似，那么你的直覺是正確的，我們E、F、G組成了的二次方的貝塞爾曲線去插值p點的時候，如果把E、F、G求得H、I，那么就可以得到P，如此這般，最后我們就會得到 由因子t影響的插值公式，下面給出了GLSL里面的插值實現算法

vec4 cubic_bezier(vec4 A, vec4 B, vec4 C, vec4 D, float t)
{
vec4 E = mix(A, B, t); // E = A + t(B - A)
vec4 F = mix(B, C, t); // F = B + t(C - B)
vec4 G = mix(C, D, t); // G = C + t(D – C)
vec4 H = mix(E, F, t); // H = E + t(F - E)
vec4 I = mix(F, G, t); // I = F + t(G - F)
vec4 P = mix(H, I, t); // P = H + t(I - H)
return P;
}
Just as the structure of the equations for a cubic Bézier curve “includes” the equations for a quadratic curve, so, too, does the code to implement them. In fact, we can layer these curves on top of each other, using the code for one to build the next

正如三次方與二次方的貝塞爾曲線的關系那樣，是包含關系，實際上，咱們的代碼也是這樣的包含關系。如下所示：

vec4 cubic_bezier(vec4 A, vec4 B, vec4 C, vec4 D, float t)
{
vec4 E = mix(A, B, t); // E = A + t(B - A)
vec4 F = mix(B, C, t); // F = B + t(C - B)
vec4 G = mix(C, D, t); // G = C + t(D - C)
return quadratic_bezier(E, F, G, t);
}
Now that we see this pattern, we can take it further and produce even higher-order curves. For example, a quintic Bézier curve (one with five control points) can be implemented as

類似的，我們可以得到更高階的曲線的推導公式，長相如下這般

vec4 quintic_bezier(vec4 A, vec4 B, vec4 C, vec4 D, vec4 E, float t)
{
vec4 F = mix(A, B, t); // F = A + t(B - A)
vec4 G = mix(B, C, t); // G = B + t(C - B)
vec4 H = mix(C, D, t); // H = C + t(D - C)
vec4 I = mix(D, E, t); // I = D + t(E - D)
return cubic_bezier(F, G, H, I, t);
}
This layering could theoretically be applied over and over for any number of control points. However, in practice, curves with more than four control points are not commonly used. Rather, we use splines.

這種形勢的曲線實際上可以一層層的嵌套下去，但是在現實中，我們很少使用有4個控制點以上的貝塞爾曲線，如果控制點比較多的使用我們使用樣條曲線

本日的翻譯就到這里，明天見，拜拜~~

第一時間獲取最新橋段，請關注東漢書院以及圖形之心公眾號

東漢書院，等你來玩哦