Matrices(矩陣)

周一到周五，每天一篇，北京時間早上7點準時更新~

The matrix is not just a Hollywood movie trilogy, but an exceptionally powerful mathematical tool that greatly simplifies the process of solving one or more equations with variables that have complex relationships with one another(矩陣不像東漢書院那樣，是個花花腸子，天天想著多圈點粉絲，完了還想兜售課程，還想推廣他們自家的引擎，簡直是不懷好意， 矩陣它能夠讓空間位置關系方面的表達得到簡化，這么看來，矩陣的確是個好人的說呢。但是比起像柯文哲這樣的喜歡把fan念成huan的，東漢書院還是至少逼格高一點的呢). One common example of this, near and dear to the hearts of graphics programmers, is coordinate transformations(矩陣這個同學比較常見的姿勢就是坐標的轉換). For example, if you have a point in space represented by x, y, and zcoordinates, and you need to know where that point is if you rotate it some number of degrees around some arbitrary point and orientation, you use a matrix(比如，你使用矩陣沿著空間中的某個軸去旋轉一個點，你需要知道這個點被轉到哪里去了). Why? Because the new x coordinate depends not only on the old x coordinate and the other rotation parameters, but also on what the y and z coordinates were(為什么？因為新的x坐標不僅僅受到原來的x坐標的影響，還會受到原來的y、z坐標的影響). This kind of dependency between the variables and solution is just the sort of problem at which matrices excel(這種類型的變量間的依賴關系剛好是矩陣所能解決的問題). For fans of the Matrix movies who have a mathematical inclination, the term “matrix” is indeed an appropriate title(對于那些有數學功底的***帝國的粉絲來說，毫無疑問matrix確實是一個非常合適的電影名稱)

Mathematically, a matrix is nothing more than a set of numbers arranged in uniform rows and columns—in programming terms, a two-dimensional array(數學意義上，矩陣就是很多行列的數據組成一坨東西，在程序員眼里，就是一個二維數組). A matrix doesn’t have to be square, but all of the rows must have the same number of elements and all of the columns must have the same number of elements(一個矩陣不必要非得是方陣，只不過要求每一行或者每一列的元素個數都相同就行). The following are a selection of matrices. They don’t represent anything in particular but serve only to demonstrate matrix structure(下面就是一系列的矩陣，他們不代表任何東西，僅僅是展示了矩陣的結構). Note that it is also valid for a matrix to have a single column or row(矩陣也可能只包含一行或者一列元素). A single row or column of numbers would more simply be called a vector, as discussed previously(如果一個矩陣只有一行或者一列，那么它可以被看成是一個向量). In fact, as you will soon see, we can think of some matrices as a table of column vectors(實際上，你將很快看到，我們可以把矩陣想象成為一個列向量組成的表)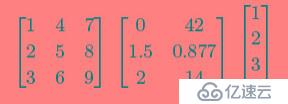

Matrix” and “vector” are two important terms that you see often in 3D graphics programming literature(在3D圖形學里，矩陣和向量是非常重要的東西). When dealing with these quantities, you also see the term “scalar.”(當處理這些數據的時候，你經常還會看到標量，一個標量就是一個表達長度的數字或者說什么其他的東西的數據) A scalar is just an ordinary single number used to represent a magnitude or a specific quantity (you know—a regular old, plain, simple number... like before you cared or had all this jargon added to your vocabulary). Matrices can be multiplied and added together, but they can also be multiplied by vectors and scalar values(矩陣間可以進行乘法加法運算，它還可以跟向量和標量進行乘法運算). Multiplying a point (represented by a vector) by a matrix (representing a transformation) yields a new transformed point (another vector)(用點和矩陣相乘可以得到一個轉換后的點). Matrix transformations are actually not too difficult to understand but can be intimidating at first(矩陣變換不是非常難理解但是剛接觸的玩家會感到很怕怕，如果是這樣的話，建議去抓住×××姐的手). Because an understanding of matrix transformations is fundamental to many 3D tasks, you should still make an attempt to become familiar with them(由于理解矩陣任然是你做很多3D工作的基礎，所以你還是要克服恐懼，適應這塊的數學內容). Fortunately, only a little understanding is enough to get you going and doing some pretty incredible things with OpenGL(幸運的是，只需要小學數學，你就可以玩轉OpenGL了). Over time, and with a little more practice and study, you will master this mathematical tool yourself.(隨著時間的推移和簡單的練習，你就會完全掌握數學工具)

In the meantime, as previously for vectors, you will find a number of useful matrix functions and features available in the vmath library(就如同前面的內容一樣，vmath庫里也包含了很多可以用于矩陣計算的函數). The source code to this library is also available in the file vmath.h in the book’s source code folder(源代碼就在vmath.h里). This 3D math library greatly simplifies many tasks in this chapter and the ones to come(這個3D數學庫真的是太棒了，它簡化了很多工作以及后面要做得事情，然而感覺這個跟學生學習沒什么關系，只是讓作者看起來他后面教學內容會簡單了). One useful feature of this library is that it lacks incredibly clever and highly optimized code!(一個非常重要的特點就是，這個庫的代碼很傻，完全沒怎么優化過) This makes the library highly portable and easy to understand(這會使得這個庫很容易被人理解，以我們的實際經驗得到的結果是，沒人會去看那些晦澀的代碼，尤其是背后有數學理論的時候，即便自己寫完都不再愿意看第二遍). You’ll also find it has a very GLSL-like syntax(你會發現它跟GLSL里的語法很像).

In your 3D programming tasks with OpenGL, you will use three sizes of matrices extensively: 2 × 2, 3 × 3, and 4 × 4(在我們的OpenGL里，你將會使用三種不同大小的矩陣，2、3、4維的方陣). The vmath library has matrix data types that match those, defined by GLSL, such as(vmath提供對應的矩陣實現代碼，如下所示：)

vmath::mat2 m1;
vmath::mat3 m2;
vmath::mat4 m3;

As in GLSL, the matrix classes in vmath define common operators such as addition, subtraction, unary negation, multiplication, and division, along with constructors and relational operators(就如同GLSL里一樣，vmath庫定義了基本的矩陣的運算操作的函數接口). Again, the matrix classes in vmath are built using templates and include type definitions for single- and double-precision floating-point, and signed- and unsigned-integer matrix types(同樣，該函數是由C++模板實現，你可以使用任意的數據類型，比如浮點、雙精度或者是×××都可以的。實際上作為一個大學生或者初級3D圖形學選手，你不會去看他的vmath實現， 這些老外寫的東西需要你具備牛X的C++基礎，才勉強能看懂他們的C++代碼，這種是極其不推薦的，學習語言是為了做項目，不是為了使用語言的高級語法，C++學習應該適可而止，重點還是回過頭來看圖形學。至于3D圖形學 方面，我們的建議是如果想深入了解，還是腳踏實地一步一步好好把你的大學工科基礎那些書都翻一遍，作者此處純粹是一筆帶過，知識含量有限)

本日的翻譯就到這里，明天見，拜拜~~

第一時間獲取最新橋段，請關注東漢書院以及圖形之心公眾號

東漢書院，等你來玩哦