您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
二叉樹:樹的每個節點最多有兩個子節點。
我們看下它的結構,有二叉鏈表結構與三叉鏈表結構,具體結果如我摘自《C++Primer》中的圖。
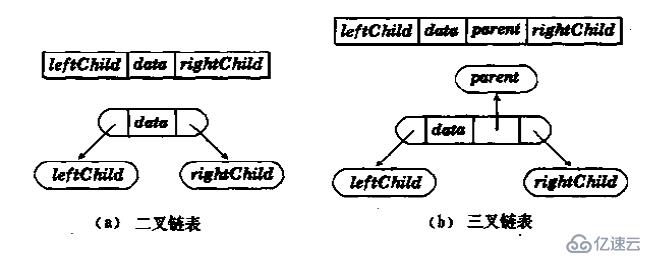
相比之下,三叉鏈表的優勢在于當我們知道父親節點要找他的子女節點比較方便和便捷,反之當我們知道子女節點找它的父親節點時也方便。
下面,我實現下二叉鏈表的結構。
template <class T>
struct BinaryTreeNode
{
BinaryTreeNode<T>* _left; //左子樹
BinaryTreeNode<T>* _right; //右子樹
T _data;
BinaryTreeNode(const T& x)
:_left(NULL)
, _right(NULL)
, _data(x)
{}
};(1)求二叉樹的葉子節點數leafsize:
葉子節點指的是,節點無子女節點。我們有兩種思路:
1)設置一下全局變量或者靜態變量的size,遍歷二叉樹,每次遇到一個節點就加加一次size
2)總葉子節點數就等于左子樹葉子節點個數+右子樹葉子節點個數
//思路1:
size_t _LeafSize(Node* root)
{
static int size = 0;
if (root == NULL)
{
return size;
}
if (root->_left == NULL && root->_right == NULL)
{
size++;
return size;
}
_LeafSize(root->_left);
_LeafSize(root->_right);
}//思路2:
size_t _LeafSize(Node* root)
{
if (root == NULL)
{
return 0;
}
if (root->_left == NULL &&root->_right == NULL)
{
return 1;
}
return _LeafSize(root->_left) + _LeafSize(root->_right);
}(2)求二叉樹的深度depth:
深度也稱作為高度,就是左子樹和右子樹深度的較大值。
size_t _Depth(Node* root)
{
if (root == NULL)
{
return 0;
}
int LeftDepth = _Depth(root->_left);
int RightDepth = _Depth(root->_right);
return LeftDepth > RightDepth ? LeftDepth +1: RightDepth+1;
}(3)求二叉樹的節點個數size:
總節點數就等于左子樹節點個數+右子樹節點個數+根節點個數1
size_t _Size(Node* root)
{
if (root == NULL)
{
return 0;
}
return _Size(root->_left) + _Size(root->_right) + 1;
}(4)求第k層節點數:
默認根節點為第一層1。
思路與求葉子節點類似。
size_t _kLevelSize(Node* root, int k)//默認根節點為第1層
{
assert(k > 0);
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
//不可以傳參數k--,不然只能是執行完這一句代碼后k才會發生變化,k一直為3
//不可以傳參數--k,執行root->_left時,k變為2,執行root->_right時為同一層k變為1
//傳參數k-1
return _kLevelSize(root->_left, k - 1) + _kLevelSize(root->_right, k - 1);
}(5)遍歷二叉樹:
注意:前中后序遍歷要不要漏掉遞歸出口。
1)前序遍歷:訪問根節點->左子樹->右子樹
void _PrevOrder(Node* root)
{
if (root == NULL)
{
return;
}
cout << root->_data << " ";
_PrevOrder(root->_left);
_PrevOrder(root->_right);
}2)中序遍歷:訪問左子樹->根節點->右子樹
void _InOrder(Node* root)
{
if (root == NULL)
{
return;
}
_InOrder(root->_left);
cout << root->_data << " ";
_InOrder(root->_right);
}3)后序遍歷:訪問左子樹->右子樹->根節點
void _PostOrder(Node* root)
{
if (root == NULL)
{
return;
}
_PostOrder(root->_left);
_PostOrder(root->_right);
cout << root->_data << " ";
}4)層次遍歷:
即一層一層地遍歷結束,再遍歷下一層節點,如int a1[10] = { 1, 2, 3, '#', '#', 4, '#', '#', 5, 6 }(注意:#表示空。)則層次遍歷就應為:1,2,5,3,4,6。
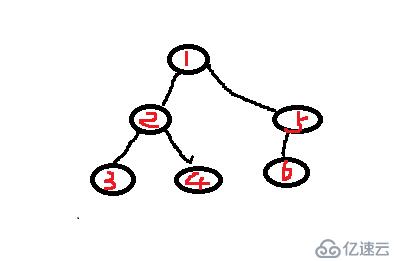
我們用隊列解決該問題:首先先給隊列無條件入隊根節點,下面在出隊根節點之前先入隊它的子女節點2、5。此時,出隊1后隊頭元素為2,在出隊它之前入隊它的根節點3,4……
void _LevelOrder(Node* root)
{
queue<Node*> q;
if (root == NULL)
{
return;
}
q.push(root);
while (!q.empty())
{
if (q.front()->_left != NULL)
{
q.push(q.front()->_left);
}
if (q.front()->_right != NULL)
{
q.push(q.front()->_right);
}
cout << q.front()->_data<< " ";
q.pop();
}
}我給出完整程序代碼(測試用例我就不要在此處多加闡述了,你們可以自己實現)。
#define _CRT_SECURE_NO_WARNINGS 1
#ifndef __TREE_H__ //防止多次包含
#define __TREE_H__
#include<iostream>
using namespace std;
#include<assert.h>
#include<queue>
#include<stack>
template <class T>
struct BinaryTreeNode
{
BinaryTreeNode<T>* _left; //左子樹
BinaryTreeNode<T>* _right; //右子樹
T _data;
BinaryTreeNode(const T& x)
:_left(NULL)
, _right(NULL)
, _data(x)
{}
};
template<class T>
class BinaryTree
{
typedef BinaryTreeNode<T> Node; //重命名在于想簡化代碼,避免過長。
public:
BinaryTree()
:_root(NULL)
{}
BinaryTree(const T* a, size_t size, const T& invalid)
:_root(NULL)
{
size_t index = 0;
_root = _CreateTree(a, size, invalid, index);
}
BinaryTree<T>(const BinaryTree<T>& t)
: _root(NULL)
{
_root = _Copy(t._root);
}
BinaryTree<T>& operator=(const BinaryTree<T>& t)
{
if (&t != this)
{
_Copy(t._root);
_Destroy(_root);
}
return *this;
}
~BinaryTree()
{
if (_root)
{
_Destroy(_root);
}
}
//前序遍歷
void PreOrder()
{
_PrevOrder(_root);
cout << endl;
}
//前序遍歷非遞歸寫法
void PreOrderNon_R()
{
_PreOrderNon_R(_root);
cout << endl;
}
//中序遍歷
void InOrder()
{
_InOrder(_root);
cout << endl;
}
//中序遍歷非遞歸寫法
void InOrderNon_R()
{
_InOrderNon_R(_root);
cout << endl;
}
//后序遍歷
void PostOrder()
{
_PostOrder(_root);
cout << endl;
}
//后序遍歷非遞歸寫法
void PostOrderNon_R()
{
_PostOrderNon_R(_root);
cout << endl;
}
//層次遍歷
void LevelOrder()
{
_LevelOrder(_root);
cout << endl;
}
//節點數
size_t Size()
{
return _Size(_root);
}
//深度(高度)
size_t Depth()
{
return _Depth(_root);
}
//葉子節點數
size_t LeafSize()
{
return _LeafSize(_root);
}
//第k層節點
size_t kLevelSize(int k)
{
return _kLevelSize(_root, k);
}
protected:
void _Destroy(Node* root)
{
if (root == NULL)
{
return;
}
if (root->_left == NULL && root->_right == NULL)
{
delete root;
root = NULL;
return;
}
_Destroy(root->_left);
_Destroy(root->_right);
}
Node* _Copy(Node* troot)
{
if (troot == NULL)
{
return NULL;
}
Node* root = new Node(troot->_data);
root->_left = _Copy(troot->_left);
root->_right = _Copy(troot->_right);
return root;
}
//方法1:
/*size_t _LeafSize(Node* root)
{
static int size = 0;
if (root == NULL)
{
return size;
}
if (root->_left == NULL && root->_right == NULL)
{
size++;
return size;
}
_LeafSize(root->_left);
_LeafSize(root->_right);
}*/
//方法2:
size_t _LeafSize(Node* root)
{
if (root == NULL)
{
return 0;
}
if (root->_left == NULL &&root->_right == NULL)
{
return 1;
}
return _LeafSize(root->_left) + _LeafSize(root->_right);
}
size_t _Size(Node* root)
{
if (root == NULL)
{
return 0;
}
return _Size(root->_left) + _Size(root->_right) + 1;
}
size_t _Depth(Node* root)
{
if (root == NULL)
{
return 0;
}
int LeftDepth = _Depth(root->_left);
int RightDepth = _Depth(root->_right);
return LeftDepth > RightDepth ? LeftDepth +1: RightDepth+1;
}
size_t _kLevelSize(Node* root,int k)//默認根節點為第1層
{
assert(k > 0);
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
//不可以傳參數k--,不然只能是執行完這一句代碼后k才會發生變化,k一直為3
//不可以傳參數--k,執行root->_left時,k變為2,執行root->_right時為同一層k變為1
//傳參數k-1
return _kLevelSize(root->_left, k-1) + _kLevelSize(root->_right, k-1);
}
Node* _CreateTree(const T* a, size_t size, const T& invalid, size_t& index)
{
Node* root = NULL;
if (index < size && a[index] != invalid)
{
root = new Node(a[index]);
root->_left = _CreateTree(a, size, invalid, ++index);
root->_right = _CreateTree(a, size, invalid, ++index);
}
return root;
}
//前序遍歷:訪問根節點->左子樹->右子樹
void _PrevOrder(Node* root)
{
if (root == NULL)
{
return;
}
cout << root->_data << " ";
_PrevOrder(root->_left);
_PrevOrder(root->_right);
}
//前序遍歷的非遞歸
void _PrevOrderNon_R(Node* root)
{
stack<Node*> s;
if (root == NULL)
{
return;
}
s.push(root);
while (!s.empty())
{
root = s.top();
cout << root->_data << " ";
s.pop();
if (root->_right)
{
s.push(root->_right);
}
if (root->_left)
{
s.push(root->_left);
}
}
}
//中序遍歷:訪問左子樹->根節點->右子樹
void _InOrder(Node* root)
{
if (root == NULL)
{
return;
}
_InOrder(root->_left);
cout << root->_data << " ";
_InOrder(root->_right);
}
//中序遍歷的非遞歸
void _InOrderNon_R(Node* root)
{
if (root == NULL)
{
return;
}
stack<Node*> s;
Node* cur = root;
Node* tmp = root;
while (cur || !s.empty())
{
while (cur)
{
tmp = cur;
s.push(cur);
cur = cur->_left;
}
cur = s.top();//將棧頂元素保存,以便于后面判斷它是否有右孩子
cout << s.top()->_data << " ";
s.pop();
if (cur->_right == NULL)
{
cur = NULL;
}
else
{
cur = cur->_right;
}
}
}
//后序遍歷:訪問左子樹->右子樹->根節點
void _PostOrder(Node* root)
{
if (root == NULL)
{
return;
}
_PostOrder(root->_left);
_PostOrder(root->_right);
cout << root->_data << " ";
}
//后序遍歷非遞歸
void _PostOrderNon_R(Node* root)
{
if (root == NULL)
{
return;
}
Node* cur = root;
Node* prev = NULL;
stack<Node*> s;
while (cur || !s.empty())
{
while (cur)
{
s.push(cur);
cur = cur->_left;
}
cur = s.top();
if (cur->_right == NULL ||cur->_right==prev )
{
cout << cur->_data << " ";
s.pop();
prev = cur;
cur = NULL;
}
else
{
cur = cur->_right;
}
}
}
//層次遍歷
void _LevelOrder(Node* root)
{
queue<Node*> q;
if (root == NULL)
{
return;
}
q.push(root);
while (!q.empty())
{
if (q.front()->_left != NULL)
{
q.push(q.front()->_left);
}
if (q.front()->_right != NULL)
{
q.push(q.front()->_right);
}
cout << q.front()->_data<< " ";
q.pop();
}
}
protected:
Node* _root;
};
#endif //__TREE_H__免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。