二叉樹的先序、中序、后序、層序遞歸及非遞歸遍歷

  二叉樹是一種樹形結構，它每個結點至多只有兩棵子樹（即二叉樹中不存在度大于2的結點）。

所謂度是結點擁有的子樹數。

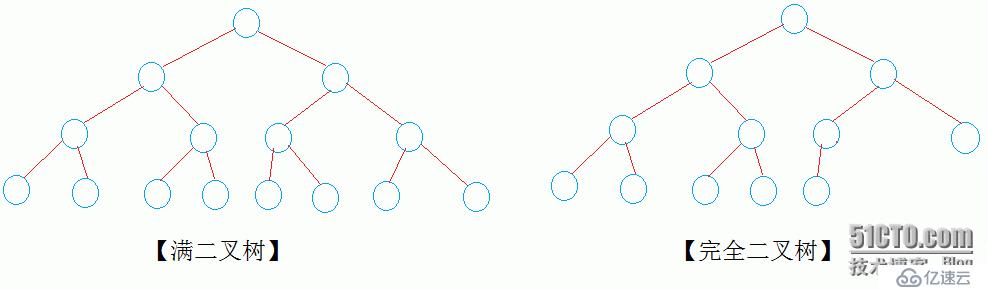
 對于二叉樹，它具有以下的性質：

1、在二叉樹的第i層上至多有2^(i-1)個結點（i>=1）。

2、深度為k的二叉樹至多有2^k-1個結點。

3、對任何一棵二叉樹，如果它的葉子結點個數為n0，度為2的結點為n2，那么m = n + 1;

  eg.如果設一個二叉樹中度為1的結點個數為n1

故總結點數   N = n0 + n1 + n2;   (1)

  二叉樹除了根結點外，其余結點都有一個分支，設M為分支總數，則 N = M + 1;由于這些分支是由度為1或2的結點射出的，則M = n1 + 2*n2;

   則有    N = n1 + 2*n2 + 1   (2)

   由（1）（2）得 n0 = n2 + 1;

4、具有n個結點的完全二叉樹的深度為∟log 2 n」+1.(其中“∟x」 ”表示不大于x的最大整數)。

5、如果對一棵有n個結點的完全二叉樹的結點按層序編號（每一層從左到右，直到∟log 2 n」+1），則對任意一結點i（1=<i<=n）有

  （1）如果i=1，則結點i是二叉樹的根，無雙親；如果i>1，則其雙親是結點∟i/2」.

  （2）如果2i>n,則結點i無左右孩子（結點i為葉子結點）否則其左孩子是結點2i；

  （3）如果2i+1>n，則結點i無左右孩子；否則其右孩子是結點2i+1；  

#pragma once
#include<queue>
#include<stack>
#include<iostream>
using namespace std;
template<class T>
struct BinaryTreeNode
{
	BinaryTreeNode<T> *_left;
	BinaryTreeNode<T> *_right;
	T _data;
public:
	BinaryTreeNode(const T& x)
		:_data(x)
		,_right(NULL)
		,_left(NULL)
	{}
};
template<class T>
class BinaryTree
{
	typedef BinaryTreeNode<T> Node;
public:
	BinaryTree()
		:_root(NULL)
	{}
	BinaryTree<T>(const T* a, size_t size, const T& invalid)
	{
		size_t index = 0;
		_root = _CreatTree(a, size, index, invalid);
	}
	BinaryTree<T>(const BinaryTree<T>& t)
	{
		_root=_Copy(t._root);
	}
	BinaryTree<T>& operator=( BinaryTree<T> t)
	{
		swap(_root, t._root);
		return *this;
	}
	~BinaryTree()
	{
		_Clear(_root);
		_root=NULL;
	}
	void PrevOrder()
	{
		cout << "先序：" << endl;
		_PrevOrder(_root);
	}
	void InOrder()
	{
		cout << "中序：" << endl;
		_InOrder(_root);
	}
	void PostOrder()
	{
		cout << "后序：" << endl;
		_PostOrder(_root);
	}
    //層序      
	//思想：隊列
	//1.先判斷根節點是否為NULL
	//2.如果根節點不為空，節點入隊（不是入值）
	//3.判斷隊列是否為空，如果不為空，出隊
	//4.判斷左 右子樹節點是否為空，
	//5.如果不為空，入隊 左右節點，跳至2
	void LeveLorder()    //層序
	{
		cout << "層序：" << endl;
		queue<Node*> tmp;
		if (_root == NULL)
			return;
		else
		{
			tmp.push(_root);
			while (!tmp.empty())
			{
				Node* Front = tmp.front();
				cout << Front->_data << " ";
				tmp.pop();
				if (Front->_left)
				{
					tmp.push(Front->_left);
				}
				if (Front->_right)
				{
					tmp.push(Front->_right);
				}
			}
		}
	}
	size_t Size()
	{
		return _Size(_root);
	}
	size_t Depth()
	{
		_Depth(_root);
	}
	size_t LeafSize()
	{
		return _leafSize(_root);
	}
	
protected:
	Node* _CreatTree(const T*a, size_t size, size_t& index, const T& invalid)
	{
		Node* root = NULL;
		if (a[index] != invalid&&index < size)
		{
			root = new Node(a[index]);
			root->_left = _CreatTree(a, size, ++index, invalid);//++index 返回index  index++返回臨時變量（在此編譯不通過）
			root->_right = _CreatTree(a, size, ++index, invalid);
		}
		return root;
	}
	//先序遍歷  遞歸形式
	void _PrevOrder(Node* root)   
	{
		if (root == NULL)
			return;
		cout << root->_data << " ";
		_PrevOrder(root->_left);
		_PrevOrder(root->_right);
	}
	//先序遍歷 非遞歸  借助棧
	//和層序實現差不多，只是一個是借助隊，一個是借助棧
	void _PrevOrder(Node* root)  
	{
		stack<Node*> cur;
		if (root == NULL)  //1.先判斷根結點是否為空
			return;
		else
		{
			cur.push(root);   //2,壓棧
			while (!cur.empty()) // 3.判斷棧是否為空，不為空，先壓右 再壓左子樹
			{
				Node* temp = cur.top();
				cout << temp->_data << " ";
				cur.pop();
				if (temp->_right)
				{
					cur.push(temp->_right);
				}
				if (temp->_left)
				{
					cur.push(temp->_left);
				}
			}
		}
	}
	 //中序遍歷   遞歸形式
	void _InOrder(Node* root)   
	{
		if (root == NULL)
			return;
		_InOrder(root->_left);
		cout << root->_data << " ";
		_InOrder(root->_right);
	}
	//中序遍歷 非遞歸  借助棧
	void _InOrder(Node* root)
	{
		Node* cur = root;
		stack<Node*> tack;
		while (cur || !tack.empty())
		{
			while (cur)
			{
				tack.push(cur);
				cur = cur->_left;
			}
			if (!tack.empty())
			{
				Node* Top = tack.top();
				tack.pop();
				cout << Top->_data <<" ";
				cur = Top->_right;
			}
		}
	}
	
	//后序遍歷  遞歸形式
	void _PostOrder(Node* root)  
	{
		if (root == NULL)
			return;
		_PostOrder(root->_left);
		_PostOrder(root->_right);
		cout << root->_data << " ";
	}
	//后序遍歷 非遞歸  借助棧
	void _PostOrder(Node* root)
	{
		Node* prev=NULL;
		Node* cur = root;
		stack<Node*> tmp;
		while (cur || !tmp.empty())
		{
			while (cur)
			{
				tmp.push(cur);
				cur = cur->_left;
			}
			Node* Top = tmp.top();
			if (Top->_right == NULL||Top->_right==prev)
			{
				cout << Top->_data << " ";
				tmp.pop();
				prev = Top;
				cur = NULL;
			}
			else
			{
				cur = Top->_right;
			}
		}
	}
	void _Size(Node* root)
	{
		if (root == NULL)
			return 0;
		return _Size(root->_left) + _Size(root->_right) + 1;
	}
	size_t _Depth(Node* root)
	{
		if (root == NULL)
			return 0;
		int leftdepth = _Depth(root->_left);
		int rightdepth = _Depth(root->_right);
		return leftdepth > rightdepth ? leftdepth + 1 : rightdepth + 1;
	}
	size_t _leafSize(Node* root)
	{
		static size_t size = 0;
		if (root == NULL)
			return 0;
		if (root->_left == NULL&&root->_right == NULL)
		{
			++size;
			return size;
		}
		_leafSize(root->_left);
		_leafSize(root->_right);
		return size;
	}
	void _Clear(Node* root)
	{
		if (root)
		{
			_Clear(root->_left);
			_Clear(root->_right);
			delete root;
		}
	}
	Node* _Copy(Node* root)
	{
		if (root==NULL)
		{
			return NULL;
		}
		Node *tem = new Node(root->_data);
		tem->_left=_Copy(root->_left);
		tem->_right=_Copy(root->_right);
		return  tem;
	}
private:
	Node* _root;
};