您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
堆是什么?剛接觸到這個概念估計都摸不著頭腦,不知道堆是什么樣個東西。簡單介紹下,
堆數據結構是一種數組對象,它可以被視為一棵完全二叉樹結構。
堆結構的二叉樹存儲有兩種情況:
(1).最大堆:每個父節點的都大于孩子節點。
(2).最小堆:每個父節點的都小于孩子節點。
舉個例子可能好理解些,看下面:
int a[] = {10,11,13,12,16,18,15,17,14,19};
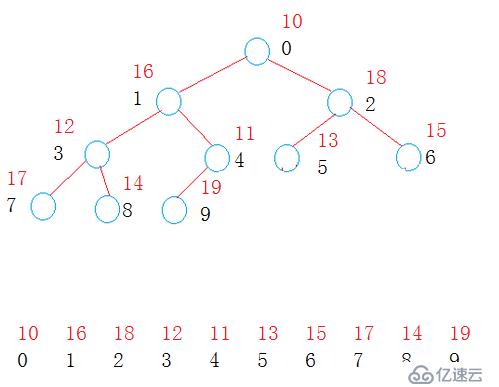
熟悉了它的結構,給解釋下怎么來構建這個堆。
對于他的實現,我們直接可以借用vector作為成員,因為使用到的數組要實現增刪查改,增容是肯定會用到的,將傳過來的數組全部push_back到vector中去,然后從最后一個非葉子節點開始向下調整,知道最后調整玩根結點,就完成了堆的構成。
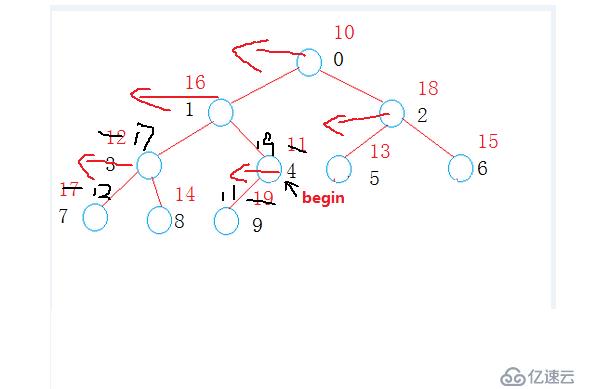
那么什么叫做向下調整了?
向下調整就是從第一個非葉子節點作為一顆子樹開始調整,將大的數據放大父節點上,依次調整,直至調整到根節點為止
#include <vector>
template <class T>
class Heap
{
public:
Heap()
{}
Heap(T* a,size_t size)
{
size_t index = 0;
while (index < size)
{
_a.push_back(a[index]);
index++;
}
for (int i = (_a.size() - 2) / 2; i >= 0; i--)
_AdjustDown(i);
}
void _AdjustDown(size_t parent)
{
size_t child = 2 * parent + 1;
while (child < _a.size())
{
//找出孩子中的最大孩子
if (child + 1 < _a.size() && _a[child] < _a[child + 1])
{
++child;
}
//把
if (_a[parent] < _a[child])
{
swap(_a[parent], _a[child]);
parent = child;
child = child * 2 + 1;
}
else
{
break;
}
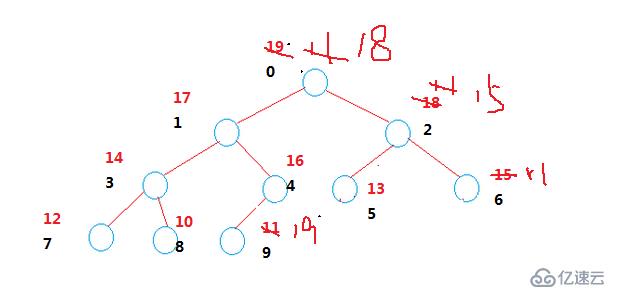
} 下面再重點介紹下pop函數的寫法,pop函數就相當于將根節點刪除了,我們轉換下思路,將根節點和最后一個節點交換,然后就需要寫一個向上調整的函數就行了。向上調整的思路:由于交換后根節點變成了最后一個節點的值,比原來根節點的左右小,所以需要用左右節點中的大值將這個小值換下來。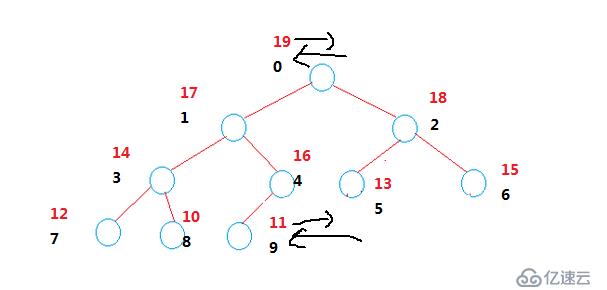
void pop()
{
size_t size = _a.size();
assert(size > 0);
swap(_a[0], _a[size - 1]);
_a.pop_back();
size = _a.size();
_AdjustDown(0);
}
void _AdjustUp(int child)
{
int parent = (child - 1) / 2;
while (parent >= 0)
{
//找出孩子中的最大孩子
if (_a[child] > _a[parent])
{
swap(_a[child], _a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}其他函數:
void push(const T& x)
{
_a.push_back(x);
_AdjustUp(_a.size() -1);
}
size_t top()
{
assert(!_a.empty());
return _a[0];
}
bool empty()
{
return _a.size() == 0;
}
size_t Size()
{
return _a.size();
}
void Print()
{
for (int i = 0; i < _a.size(); i++)
{
cout << _a[i] << " ";
}
cout << endl;
}免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。