您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
在標準庫算法中,next_permutation可以計算一組數據的全排列,下面是簡單的剖析
首先查看STL中函數原型:
template <class BidirectionalIterator> bool next_permutation (BidirectionalIterator first, BidirectionalIterator last ); template <class BidirectionalIterator, class Compare> bool next_permutation (BidirectionalIterator first, BidirectionalIterator last, Compare comp);
兩個重載函數。第二個帶謂詞參數comp,默認謂詞函數為“”
下面為一個例子:
#include <iostream>
#include <algorithm>
using namespace std;
typedef bool (*COMP)(int,int);
bool Compare(int a,int b)
{
return !(a<b);
}
int main()
{
int a[] = {3,1,2};
COMP comp=Compare;
do{
cout << a[0] << " " << a[1] << " " << a[2] << endl;
}while (next_permutation(a,a+3,comp));
return 0;
}運行結果:
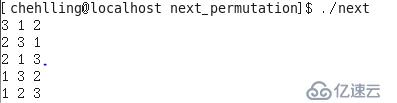
下圖是在Linux下stl_algo.h中next_permutation的部分代碼:
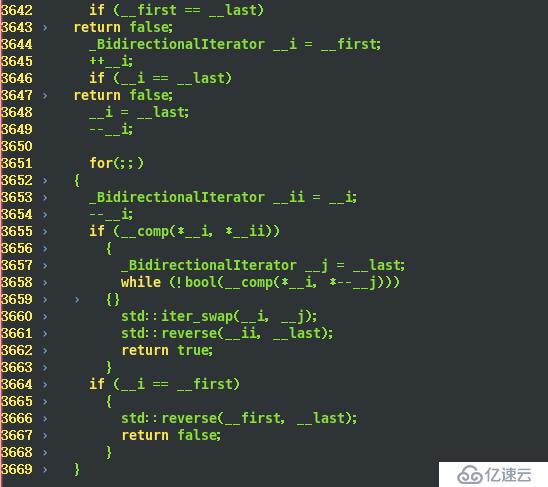
如果要比較的數列中只有一個元素的話返回直接false;否則使變量__i指數列的最后一個元素,進入循環 ;
從最右邊邊開始比較倆個相鄰的元素,直到找到左邊比右邊小的那兩個數,左邊那個就是待交換的數
再從最右邊開始,找比代替換的那個數大的第一個元素,然后交換這兩個數,交換之后反轉被替換元素之后的所有元素
原排列 中間轉換 值
1,2,3,4 3,2,1 ((3 * (3) + 2) * (2) + 1) * (1) = 23
1,2,4,3 3,2,0 ((3 * (3) + 2) * (2) + 0) * (1) = 22
1,3,2,4 3,1,1 ((3 * (3) + 1) * (2) + 1) * (1) = 21
1,3,4,2 3,1,0 ((3 * (3) + 1) * (2) + 0) * (1) = 20
1,4,3,2 3,0,1 ((3 * (3) + 0) * (2) + 1) * (1) = 19
. . .
. . .
. . .
4,3,2,1 0,0,0 ((0 * (3) + 0) * (2) + 0) * (1) = 0
| | | | | |
| | | |
| |
上面的中間轉換指的是:每一個數字后面比當前位數字大的數字的個數。比如:
1,3,4,2 中,1 后面有(3, 4, 2) 他們都大于1,所以第一位是 3
3 后面有(4, 2), 但只有4大于3,所以第二位是 1
4 后面有(2), 沒有比4 大的,所以第三位是 0
最后一位后面肯定沒有更大的,所以省略了一個0。
經過這種轉換以后,就得到了一種表示方式(中間轉換),這種表達方式和原排列一一對應,可以相互轉化。
仔細觀察這種中間表達方式,發現它的第一位只能是(0,1,2,3),第二位只能是(0,1,2),第三位只能是(0,1)。通常,數字是用十進制表示的,計算機中用二進制,但是現在,我用一種特殊的進制來表示數:
第一位用1進制,第二位用2進制,第三位用3進制
于是就得到了這種中間表示方式的十進制值。如:
階
| | |
1,1,0 ----> ((1 * (3) + 1) * (2) + 0) * (1) = 8
3,1,0 ----> ((3 * (3) + 1) * (2) + 0) * (1) = 20
這樣,就可以得到一個十進制數和一個排列之間的一一對應的關系。
現在排列數和有序的十進制數有了一一對應的關系(通過改變對應關系,可以使十進制數升序)。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。