您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
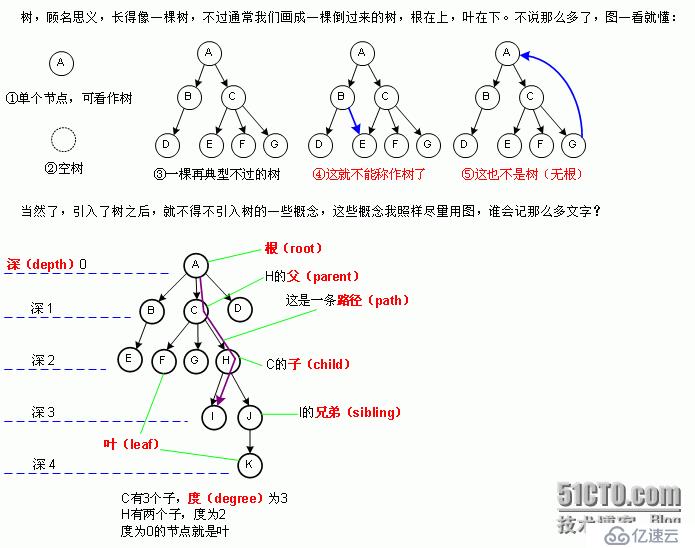
樹相關的一些概念。
樹是n(n>=0)個有限個數據的元素集合,形狀像一顆倒過來的樹。
結點:結點包含數據和指向其它結點的指針。
結點的度:結點擁有的子節點個數。
葉子節點:沒有子節點的節點(度為0)。
父子節點:一個節點father指向另一個節點child,則child為孩子節點,father為父親結點。
兄弟節點:具有相同父節點的節點互為兄弟節點。
節點的祖先:從根節點開始到該節點所經的所有節點都可以稱為該節點的祖先。
子孫:以某節點為根的子樹中任一節點都稱為該節點的子孫。
樹的高度:樹中距離根節點最遠結點的路徑長度。
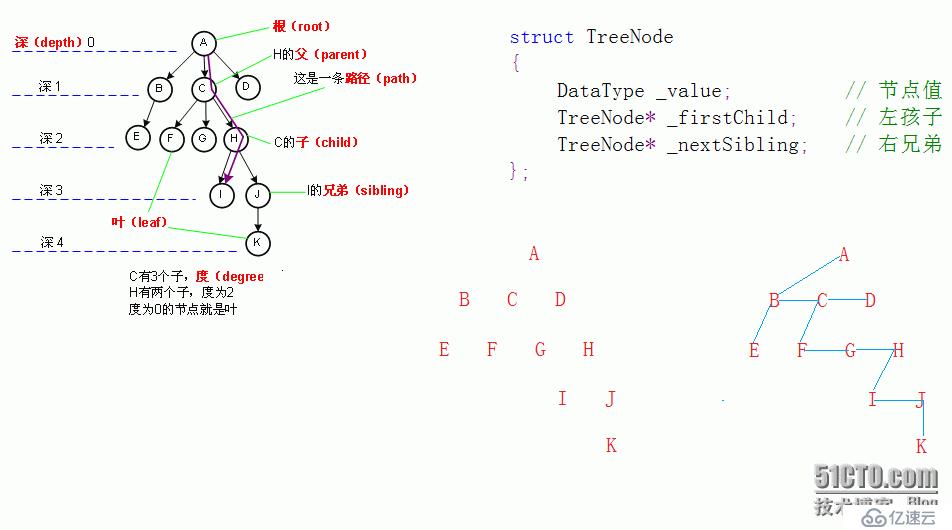
樹的存儲結構:
二叉樹的結構
二叉樹:二叉樹是一棵特殊的樹,二叉樹每個節點最多有兩個孩子結點,分別稱為左孩子和右孩子。
滿二叉樹:高度為N的滿二叉樹有2^N - 1個節點的二叉樹。
完全二叉樹: 若設二叉樹的深度為h,除第 h 層外,其它各層 (1~h-1) 的結點數都達到最大個數,第 h 層所有的結點都連續集中在最左邊,這就是完全二叉樹
前序遍歷(先根遍歷):
(1):先訪問根節點;
(2):前序訪問左子樹;
(3):前序訪問右子樹;
中序遍歷:
(1):中序訪問左子樹
(2):訪問根節點;
(3):中序訪問右子樹;
后序遍歷(后根遍歷):
(1):后序訪問左子樹;
(2):后序訪問右子樹;
(3):訪問根節點;
層序遍歷:
(1):一層層節點依次遍歷。
下面是二叉樹的具體實現:
template<class T>
struct BinaryTreeNode
{
BinaryTreeNode<T > *_left;
BinaryTreeNode<T > *_right;
T _data;
};
template<class T>
class BinaryTree
{
Typedef BinaryTreeNode< T> Node;
protected:
Node *_root;
public:
BinaryTree() //無參構造函數
:_root( NULL)
{
}
BinaryTree( const T *a, size_t size, const T& invalid)
{
size_t index = 0;
_root = _CreateTree( a, size , invalid, index);
}
protected:
Node *__CreateTree( const T *a, size_t size, const T& invalid, size_t &index )
{
Node *root = NULL;
if (index < size && a[index ] != invalid) //是有效值時
{
root = new Node(a [index]);
root->_left = __CreateTree( a, size , invalid, ++ index);
root->_right = __CreateTree( a, size , invalid, ++index);
}
return root;
}
//前序遍歷--------遞歸寫法,缺點是:有大量的壓棧開銷。
void Prevorder(Node *root )
{
if (root == NULL)
{
return;
}
else
{
cout << root->_data << " " ;
_prevorder( root->_left);
_prevorder( root->_right);
}
}
//前序遍歷------------非遞歸寫法
//前序遍歷的非遞歸寫法思想:需要借助棧。
void PrevOrderRonR()
{
stack<Node*> s;
if (_root == NULL )//根結點為空的話直接return掉即可。
{
return;
}
if (_root)
{
s.push(_root); //根不為空的時候將根結點進行壓棧。
}
while (!s.empty())//判斷棧是否為空
{
Node *top = s.top(); //棧不為空,則取棧頂元素
cout << top->_data << " ";//然后進行訪問棧頂元素
s.pop(); //訪問完棧頂元素將其從棧中pop掉。
if (top->_right)//要根據棧進行先序遍歷,則必須是先訪問根節點,再訪問左子樹,最后訪問右子樹,因為棧是“后進先出的”,要想先訪問左子樹,則必須先入右子樹,再入左子樹。如果棧頂元素的右子樹不為空,
{
s.push(top->_right); //棧頂的右子樹不為空,將其進行壓棧。
}
if (top->_left)
{
s.push(top->_left); //棧頂的左子樹不為空,將其進行壓棧。
}
}
cout << endl;
}
//中序遍歷----------遞歸寫法
void _Inorder(Node *root )
{
if (root == NULL)
{
return;
}
else
{
_Inorder(Node * root)
{
if (root == NULL )
{
return;
}
else
{
_Inorder(root->_left);
cout << root->_data << " " ;
Inorder(root->_right);
}
}
}
}
//中序遍歷的非遞歸寫法,思想是:也是借助棧,主要核心是找最左結點,定義一個cur指針,讓它最開始指向_root。
void TnOrderNonR()
{
stack<Node*> s;
Node *cur = _root;
while (cur || !s.empty())
{
whie(cur) //找最左結點
{
s.push(cur); //將cur壓棧。
cur = cur->_left; //cur指向它的左孩子
}
Node *top = s.top();
cout << top->_data << " ";
s.pop();
cur = top->_right;
}
}
//后序遍歷---------遞歸寫法
void Postorder(Node *root )
{
if (root == NULL)
{
return;
}
else
{
Postorder( root->_left);
Postorder( root->_right);
cout << root->_data << " " ;
}
}
//后序遍歷----------非遞歸寫法,思想是:先找最左結點,找到后但不能訪問最左結點,要先判斷最左結點的右子樹是否為空,若為空, 則可以訪問最左結點,否則不可以訪問最左結點,需要訪問右子樹。
//可以訪問根結點的條件:上一層訪問的節點為右子樹。所以我們需要定義兩個指針prev與cur ,cur用來保存當前結點,prev用來保存上一層訪問的結點。
void PostOrderNonR()
{
stack<Node*> s;
Node *prev = NULL;
Node *cur = _root;
while (cur || !s.empty())
{
while (cur)//找最左結點
{
s.push(cur);
cur = cur->_left;
}
Node *top = s.top(); //定義一個棧頂指針,用來指向棧頂元素。
if (top->_right == NULL || top->_right == prev)//棧頂節點的右子樹為空或者上一次訪問的節點為右子樹,則可以訪問棧頂元素。
{
cout << top->_data << " " ;
s.pop();
prev = top;
}
else
{
cur = top->_left;
}
}
}
//二叉樹的層序遍歷(即是一層一層的進行遍歷):思想是:需要借助隊列,首先取隊頭,判斷它是否為空,若為空直接return;不為空的時候,進行入隊操作。
//如何取到隊頭?入數據還是入指針?最好入指針,需要保存數據或者節點的時候最好入指針。
void LevelOrder()
{
queue<Node*> q;
if (_root == NULL )
{
return;
}
q.push(_root);
while (!q.empty())
{
Node *front = q.front(); //取隊頭元素
q.pop();
cout << front->_data<< " ";
if (front->_left)//隊頭元素的左孩子不為空的時候,將它的左孩子壓入隊列
{
q.push(front->_left);
}
if (front->_right)//隊頭元素的右孩子不為空的時候,將它的右孩子壓入隊列
{
q.push(front->_right);
}
}
}
size_t _Depth(Node *root )//思想:當前深度=(左子樹和右子樹中深度較大的一個)+1;
{
if(root == NULL)
{
return 0;
}
int left = _Depth(root->_left);
int right = _Depth(root ->_right);
return left > right ? left + 1 : right + 1;
}
size_t _GetKLevel(Node *root , size_t K)//取第K層結點,遞歸寫法。
{
if (root == NULL)
{
return 0;
}
if (K == 1)
{
return 1;
}
return _GetKLevel(root ->_left, K - 1) + _GetKLevel(root->_right, K - 1);
}
Node* _Find(Node * root, const T& x)//查找結點為x的結點
{
if (root == NULL)
{
return NULL ;
}
if (root ->_data == x)
{
return root ;
}
Node *ret = _Find( root->_left, x );
if (ret)
{
return ret;
}
else
{
return _Find(root ->_right, x);
}
}
size_t _leafsize(Node *root )//求葉子節點的個數,思想:左子樹的葉子結點數目+右子樹的葉子結點的數目。
{
if (root == NULL)
{
return 0;
}
if (root ->_left == NULL&& root->_right == NULL )
{
return 1;
}
return _leafsize(root ->_left) + _leafsize(root->_right);
}
//遞歸即是=子問題+返回條件
//方法一:
size_t _size(Node *root )//結點的數目
{
if (root == NULL)
{
return 0;
}
return _size(root ->_left) + _size(root->_right) + 1;
}
//方法二:遍歷法
size_t _size(Node *root)
{
static size_t sSize = 0;//此句代碼會讓程序有線程安全問題
if (root == NULL )
{
return sSize;
}
++sSize;
_size(root->_left);
_size(root->_right);
return sSize;6
}
};
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。