您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
關于根底單薄的讀者,本節的內容能夠略顯流暢和單調,假如認為費勁,可以臨時跳過,用到的時分再來瀏覽。然則本節所講的內容是進修編程的根底,是程序員的根本功,即便如今不學,遲早也要回來學。
后面兩節對二進制、八進制和十六進制停止了闡明,接下來講一下分歧進制之間的數字是若何轉換的,這在編程中常常會用到,特別是C言語。
二進制、八進制和十六進制向十進制轉換多是十分輕易的,就是“按權相加”。
所謂“權”,也即“位權”。例如,十進制第1位的位權為100=1,第2位的位權為101=10,第3位的位權為102=100;而二進制第1位的位權為20=1,第2位的位權為21=2,第3位的位權為22=4。設數字所采取的進制為N(基數也是N),那么第 i 位的位權為 N(i-1)。
分歧進制轉換為十進制舉例:
二進制:1001 = 1×23 + 0×22 + 0×21 + 1×20 = 8 + 0 + 0 + 1 = 9
二進制:101.1001 = 1×22 + 0×21 + 1×20 + 1×2-1 + 0×2-2 + 0×2-3 + 1×2-4 = 4 + 0 + 1 + 0.5 + 0 + 0 + 0.0625 = 5.5625
八進制:0302 = 3×82 + 0×81 + 2×80 = 192 + 0 + 2 = 194
八進制:0302.46 = 3×82 + 0×81 + 2×80 + 4×8-1 + 6×8-2 = 192 + 0 + 2 + 0.5 + 0.09375= 194.59375
十六進制:0Xea7 = 14×162 + 10×161 + 7×160 = 3751
上節的表格中給出了復雜的十進制和二進制的轉換關系,要想取得更多的轉換關系,可以運用輾除法。輾除法也就是“除模取余”法。除模取余就是將一個幾進制的數轉化成另一個進制時, 另一個進制的基數就是模,用將要轉化的進制數除以模,取它的余數。
下圖以十進制的“19”轉換為二進制為例停止解說:

圖1:19 轉換為二進制
如圖所示,以2為除數,不斷相除下去,直到商為0,余數則為求得的二進制數。
留意:余數要倒序陳列,也就是說,最先求得的余數排在二進制的最初面,最初求得的余數排在二進制的最后面。下面的例子中,最初求得的二進制數為 10011。
固然其他進制也可以依照輾除法來轉換,然則比擬費事,下面引見更復雜的辦法。
二進制向八進制的轉換是每三位二進制數轉換為一位八進制數,運算的次序是從低位向高位順次停止,高位缺乏三位用零彌補。以二進制“1011101”為例,如下圖所示:
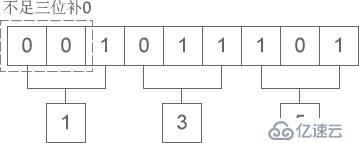
圖2:二進制轉八進制
轉換的后果為:1011101 = 0135
八進制向二進制轉換的思緒是八進制的一位轉換為二進制的三位,運算的次序是從低位向高位順次停止。異樣以八進制“0135”為例,如下圖所示:
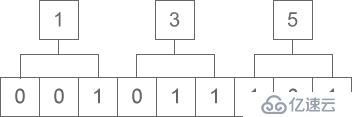
圖3:八進制轉二進制
轉換的后果為:0135 = 1011101
二進制向十六進制轉換時,四位轉換成十六進制的一位,運算的次序是從低位向高位順次停止,高位缺乏四位用零補。以“1110011”轉換成十六進制為例,如下圖所示:
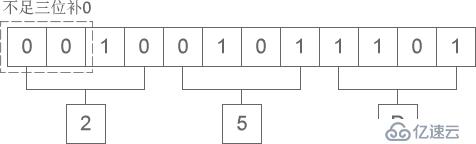
圖4:二進制轉十六進制
轉換的后果為:1001011101 = 0X25D
十六進制向二進制轉換,就是把十六進制的一位轉換成二進制的四位,留意運算的次序是從低位向高位順次停止。異樣以十六進制“0X25D”為例,如下圖所示:
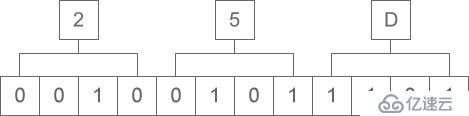
圖5:十六進制轉二進制
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。