您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
一、漢諾塔
下面是一段關于漢諾塔游戲的介紹:
/*
漢諾塔:漢諾塔(又稱河內塔)問題是源于印度一個古老傳說的益智玩具。大梵天創造世界的時候做了三根柱子,在一根柱子上從下往上按照大小順序摞著64片黃金圓盤。大梵天命令婆羅門把圓盤從下面開始按大小順序重新擺放在另一根柱子上。并且規定,在小圓盤上不能放大圓盤,在三根柱子之間一次只能移動一個圓盤。
*/
簡單來說,它的規則就是:每個盤之上不能托比當前盤大小還要大的盤。 在滿足這個規則的前提下,要將一端(A端)的所有盤移動到另一端(C)
二、游戲思路
假設有1個盤:則經過的步驟為: A -> C 1步即可
而假設有2個盤,則需要: A -> B , A -> C, B -> C ,總共3步
假設有3個盤,則步驟為:
A -> C, A -> B, C -> B, A -> C, B -> A, B -> C, A -> C
一共7步。
似乎能總結出層數和最少的如下規律:
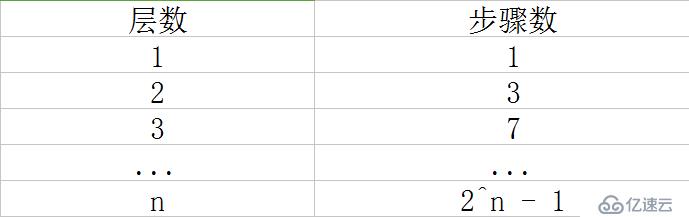
事實上,的確如此。
三、編程思路
現在如果要求實現一個函數,根據輸入的層數n,求出將當前漢諾塔從A移動到C的最少步數,則甚至不需要用程序進行推算,直接用上面的公式 : 2|^ n - 1 即可。
但如果在上述要求的前提下,還要求出具體的做法,或者說要求每一步的具體步驟,則需要讓程序自己進行推算,具體過程如下:
當層數為1層的時候,可以直接讓當前盤從A移動到C,
當層數為2層的時候,將塔尖移動到B,將底座移動到C,然后將塔尖從B移動到C即可,
而對于大于2層的情況,也可以套用當前的思路:
可以將最上面的一層看作“塔尖”,將剩下的部分看作“底座”
我們要做的仍然是將“塔尖”移動到B,將“底座”移動到C,再將B處的塔尖移動到C。
代碼如下:
void HanoiStep(int n, char A, char B, char C)
{
static int step = 1;
if(n == 1)
{
//A to C
}
else
{
PseduCode(n - 1, A, C, B); //將A處的“塔尖”移動到B
std::cout << "step" << step++ <<":" << "move " << A << " to " << C << endl;////將A處的“底座”移動到C
PseduCode(n - 1, B, A, C); //將B處的“底座”移動到C
}
}免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。