順序統計中值---無序找第k大/小值

問題描述：無序找第k小的數？

1、解法一

  先排好序，再找第k小個數；返回A[k-1]；此解法的時間復雜度為：O(nlogn)；

2、解法二

  情況一：k = 1 和 k = n 就是找數組的最小值和最大值；

  情況二：找出中位數

3、找中位數(隨機選擇算法)

  利用快速排序的原理，一輪排序，有2種情況：

  if i = k-1；返回a[i]；

  if i != k-1；左邊/右邊遞歸查找，時間復雜度為：O(n)；

具體思想：

  分析：在大多數情況下的時間復雜度是：O(n)；但是最壞情況，完全順序下找第k = n-1大數，此時的時間復雜度是：O(n^2)；

4、無序找第k小值

  快排的升序實現思想，在加上遞歸查找；

  (1)、代碼實現

#include<stdio.h>

void findKSmall(int *a, int start, int end, int key);

void findKSmall(int *a, int start, int end, int key){
    int i = start;
    int j = end;
    int tmp = a[i];
//快排中的升序
    while(i < j){
        while(i < j && a[j] > tmp){
            j--;
        }
        if(i < j){
            a[i++] = a[j];
        }
        while(i < j && a[i] < tmp){
            i++;
        }
        if(i < j){
            a[j--] = a[i];
        }
    }
    a[i] = tmp;

    if(key-1 < i){
        findKSmall(a, 0, i-1, key);
    }else if(key-1 > i){
        findKSmall(a, i+1, end, key);
    }else{
        return;
    }
}

void main(void){
    int a[] = {8, 4, 6, 9, 2, 3, 7, 9, 11, 10};
    int count = sizeof(a)/sizeof(int);
    int k;
    int i;

    printf("請輸入要查找的第k小的數：");
    scanf("%d", &k);
    findKSmall(a, 0, count-1, k);
    for(i = 0; i < count; i++){
        printf("%d ", a[i]);
    }

    printf("\n%d\n", a[k-1]);

}

  結果截圖

5、無序找第k大值

  快排的降序實現思想，在加上遞歸查找；

  (1)、代碼實現

#include<stdio.h>

void findKBigger(int *a, int start, int end, int key);

void findKBigger(int *a, int start, int end, int key){
    int i = start;
    int j = end;
    int tmp = a[i];
//快排中的降序
    while(i < j){
        while(i < j && a[j] < tmp){
            j--;
        }
        if(i < j){
            a[i++] = a[j];
        }
        while(i < j && a[i] > tmp){
            i++;
        }
        if(i < j){
            a[j--] = a[i];
        }
    }
    a[i] = tmp;

    if(key-1 < i){
        findKBigger(a, 0, i-1, key);
    }else if(key-1 > i){
        findKBigger(a, i+1, end, key);
    }else{
        return;
    }
}

void main(void){
    int a[] = {8, 4, 6, 9, 2, 3, 7, 9, 11, 10};
    int count = sizeof(a)/sizeof(int);
    int k;
    int i;

    printf("請輸入要查找的第k大的數：");
    scanf("%d", &k);
    findKBigger(a, 0, count-1, k);
    for(i = 0; i < count; i++){
        printf("%d ", a[i]);
    }

    printf("\n%d\n", a[k-1]);

}

  (2)、結果截圖

6、線性算法

  (1)、劃分為5個一組的元素，在找出每一組的中值(對這5個數進行排序，找出中值)，時間復雜度：O(n)

  (2)、用遞歸去找這些中值中的那一個中值(中值中的中值)；

  (3)、此時用這個最中值的下標和k作比較，之后和上面的隨機選擇算法一樣！！！

具體模型如下：

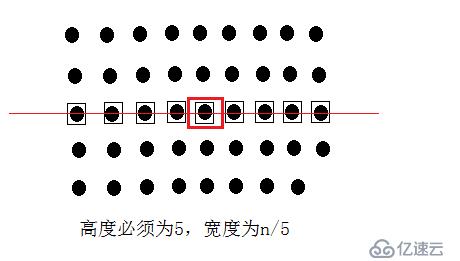
算法分析

  找中值和第k小數時間復雜度均為：O(n)；比較好的解決了上述最壞時間復雜度為O(n^2)的情況；

  3個元素一組的話，結果不成立；

  5是這個算法能成功的最小數字，7個元素為一組算法也能成立，但是性能不會有所提高；