您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
思考:通用樹結構的實現太過復雜(樹中每個結點都可以有任意多的孩子,具有多種形態),工程中很少會用到如此復雜的樹是否可以簡化呢?
思路:減少樹結點中孩子的數量。但這樣樹是否還能通用呢?
雙親孩子表示法: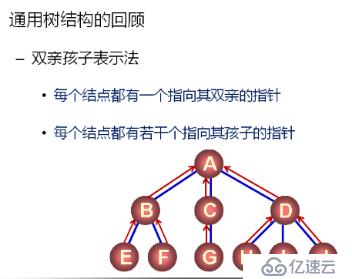
孩子兄弟表示法: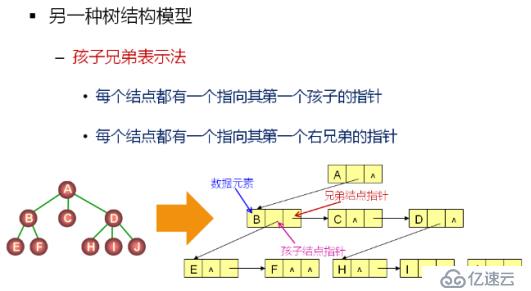
孩子兄弟表示法的特點:
1.能夠表示任意的樹形結構
2.每個結點包含一個數據成員和兩個指針成員
3.孩子結點指針和兄弟結點指針構成“樹杈”
二叉樹是由n(n>=0)個節點組成的有限集合,該集合或者為空,或者是由一個根結點加上兩顆分別稱為左子樹和右子樹的、互不相交的二叉樹組成。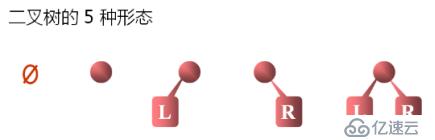
滿二叉樹:
如果二叉樹中所有分支結點的度數都為2,且葉子結點都在同一層次上,則稱這類二叉樹為滿二叉樹。
完全二叉樹:
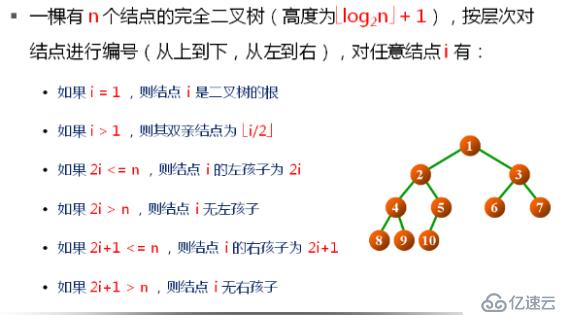
如果一棵具有N個結點高度為K的二叉樹,它的每一個結點與高度為K的滿二叉樹中編號1~n的結點一一對應,則稱這顆二叉樹為完全二叉樹。(從上到下,從左到右編號)。
完全二叉樹的特性:
同樣結點的二叉樹,完全二叉樹的高度最小;完全二叉樹的葉結點一定出現在最下面兩層。
1.最底層的葉結點一定出現在左邊;
2.倒數第二層的葉結點一定出現在右邊;
3.完全二叉樹中度數為1的結點只有左孩子。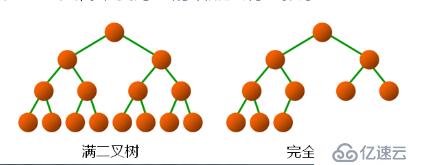
總結:
1.通用樹結構采用了雙親結點表示法進行描述;
2.孩子兄弟表示法也有能力描述任意類型的樹結構;
3.孩子兄弟表示法能夠將通用樹轉化為二叉樹(最多有兩個孩子);
1.在二叉樹的第i層最多有2^(i-1)個結點(i>=1);
2.高度為K的二叉樹最多有2^k - 1個結點(K>=0);
3.對于任何一顆二叉樹,如果其葉結點有n0個,度為2的非葉結點有n2個,則有n0 = n2 + 1;
推導證明:
n1 + 2n2 = n-1 ==> n1 + 2n2 = n0 + n1 + n2 - 1 ==> n0 = n2 + 1
4.具有n個結點的完全二叉樹的告訴為【log2N】 + 1 (【x】表示不大于x的最大整數)
5.
目標:完成二叉樹和二叉樹結點的存儲設計;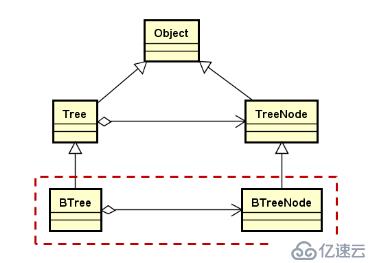
設計要點:
1.BTree為二叉樹,每個結點最多只有兩個后繼結點;
2.BTreeNode只包含4個固有的公有成員:(數據成員、指向左孩子和右孩子的指針、指向父節點的指針)
BTreeNode的設計
直接繼承自抽象樹結點,使用工廠模式(標識使用的堆空間,方便使用智能指針進行釋放)。
template < typename T >
class BTreeNode : public TreeNode<T>
{
public:
BTreeNode<T>* left;
BTreeNode<T>* right;
static BTreeNode<T>* NewNode()
{
BTreeNode<T>* ret = new BTreeNode<T>();
if(ret != NULL)
{
ret->m_flag = true; //在堆空間中申請了結點,則將該標識置為true
}
return ret;
}
~BTreeNode(){}
};BTree的設計
繼承自抽象樹結構,并組合使用BTreeNode.
template < typename T >
class BTree : public Tree<T>
{
};二叉樹的實現架構: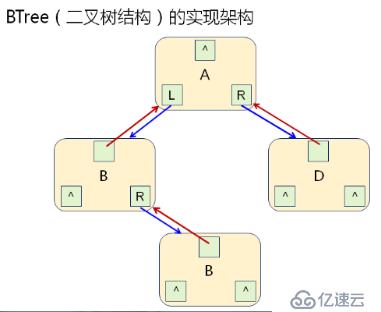
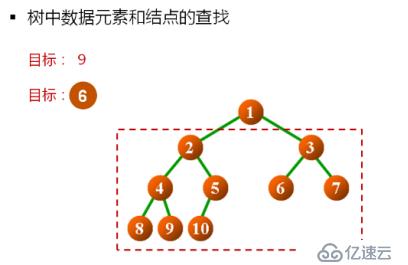
1.基于數據元素值的查找:
BTreeNode<T>* find(const T& value) const
virtual BTreeNode<T>* find(BTreeNode<T>* node, const T& value) const
{
BTreeNode<T>* ret = NULL;
if(node != NULL) // 判斷是否為空樹
{
if(node->value == value) //比較根結點
{
ret = node;
}
else
{
if(ret == NULL)
{
//遞歸查找左子樹
ret = find(node->m_left, value);
}
if(ret == NULL)
{
//遞歸查找右子樹
ret = find(node->m_right, value);
}
}
}
return ret;
}
BTreeNode<T>* find(const T& value) const
{
return find(root(), value);
}2.基于結點的查找:
BTreeNode<T> find(TreeNode<T> node) const
virtual BTreeNode<T>* find(BTreeNode<T>* node, BTreeNode<T>* obj) const
{
BTreeNode<T>* ret = NULL;
if(node != NULL) // 判斷是否為空樹
{
if(node == obj) //比較根結點
{
ret = node;
}
else
{
if(ret == NULL)
{
//遞歸查找左子樹
ret = find(node->m_left, obj);
}
if(ret == NULL)
{
//遞歸查找右子樹
ret = find(node->m_right, obj);
}
}
}
return ret;
}
BTreeNode<T>* find(TreeNode<T>* node) const
{
return find(root(), dynamic_cast<BTreeNode<T>*>(node));
}思考:是否能在二叉樹的任意結點處插入子結點?
因為二叉樹的定義中,每個結點最多只能有兩個子結點,所以必然不能在任意結點處插入,因此需要制定新的數據元素(新結點)的插入位置。
二叉樹結點的位置定義:
enum BTreeNodePos
{
ANY,
LEFT,
RIGHT
};
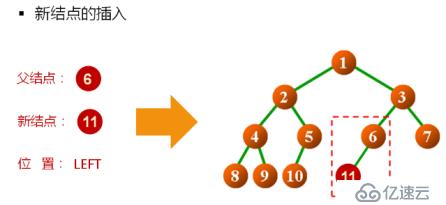
1.定義功能函數,指定位置的結點插入:virtual bool insert(BTreeNode<T>* newnode, BTreeNode<T>* node, BTNodePos pos)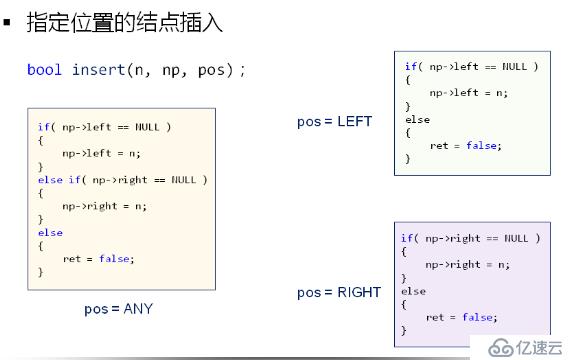
virtual bool insert(BTreeNode<T>* n, BTreeNode<T>* np, BTreeNodePos pos)
{
bool ret = true;
//指定的插入位置為ANY(沒有指定插入位置)
if(pos == ANY)
{
if(np->m_left == NULL) // 左子樹結點為空,插入到左子樹
{
np->m_left = n;
}
else if(np->m_right == NULL) // ...
{
np->m_right = n;
}
else
{
ret = false;
}
}
// 指定插入到左孩子結點
if(pos == LEFT)
{
if(np->m_left == NULL)
{
np->m_left = n;
}
else
{
ret = false;
}
}
// 指定插入到右孩子結點
if(pos == RIGHT)
{
if(np->m_right == NULL)
{
np->m_right = n;
}
else
{
ret = false;
}
}
return ret;
}2.插入新結點
bool insert(TreeNode<T>* node, BTreeNodePos pos)
bool insert(TreeNode<T>* node)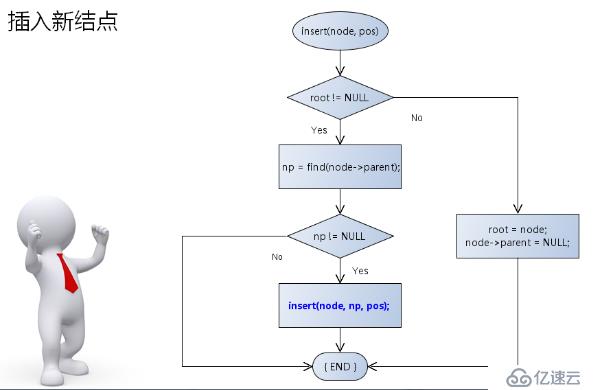
//插入結點,并指定位置
bool insert(TreeNode<T>* node, BTreeNodePos pos)
{
bool ret = true;
if(node != NULL)
{
if(root() == NULL) //判斷根結點處是否可以插入
{
node->m_parent = NULL;
this->m_root = node;
}
else
{
BTreeNode<T>* np = find(node->m_parent); //查找父節點是否存在
if(np != NULL)
{
// 調用二叉樹插入操作功能函數
ret = insert(dynamic_cast<BTreeNode<T>*>(node), np, pos);
}
else
{
THROW_EXCEPTION(InvaildParameterException, "invalid parent tree node...");
}
}
}
else
{
THROW_EXCEPTION(InvaildParameterException, "param con't be NULL...");
}
return ret;
}
//插入結點,無位置要求
bool insert(TreeNode<T>* node)
{
return insert(node, ANY);
}3.插入數據元素
bool insert(const T& value,TreeNode<T>* parent, BTreeNodePos pos)
bool insert(const T& value,TreeNode<T>* parent)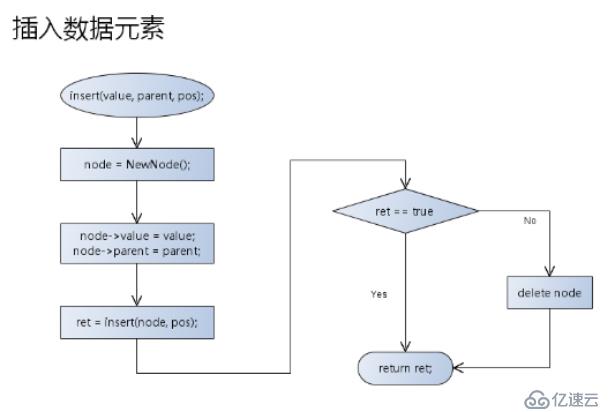
//插入數據元素,指定位置
bool insert(const T& value,TreeNode<T>* parent, BTreeNodePos pos)
{
bool ret = true;
BTreeNode<T>* node = BTreeNode<T>::NewNode();
if(node != NULL)
{
node->value = value;
node->m_parent = parent;
insert(node, pos);
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "no memory to create new tree node...");
}
return ret;
}
bool insert(const T& value,TreeNode<T>* parent)
{
return insert(value, parent, ANY);
}測試技巧:從葉結點到根結點為線性數據結構,可以使用鏈表的遍歷方式。
總結:
1.二叉樹的插入操作需要指明插入的位置;
2.插入操作必須正確處理指向父節點的指針
3.插入數據元素時需要從堆空間中創建結點,讓數據元素插入失敗時,需要釋放結點空間。
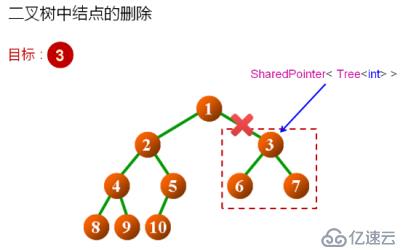
1.刪除操作功能定義
void remove(BTreeNode<T> node, BTree<T>& ret)
將node為根結點的子樹從原來的二叉樹中刪除,ret作為子樹返回(ret指向堆空間中的二叉樹對象)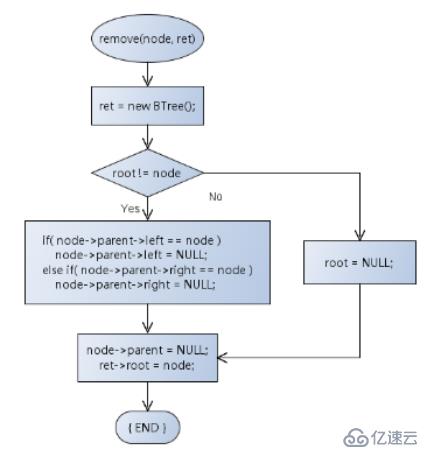
virtual void remove(BTreeNode<T>* node, BTree<T>*& ret)
{
ret = new BTree();
if(ret != NULL)
{
if(root() == node)
{
this->m_root = NULL;
}
else
{
BTreeNode<T>* np = dynamic_cast<BTreeNode<T>*>(node->m_parent);
if(np->m_left == node)
{
np->m_left = NULL;
}
else if(np->m_right == node)
{
np->m_right = NULL;
}
node->m_parent = NULL;
}
ret->m_root = node;
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "no memory to create new tree...");
}
}
2.基于數據元素的刪除
SharedPointer< Tree<T> > remove(const T& value)
SharedPointer< Tree<T> > remove(const T& value)
{
BTree<T>* ret = NULL;
BTreeNode<T>* node = find(value);
if(node != NULL)
{
remove(node, ret);
m_queue.clear();
}
return ret;
}3.基于結點的刪除
SharedPointer< Tree<T> > remove(TreeNode<T>* node)
SharedPointer< Tree<T> > remove(TreeNode<T>* node)
{
BTree<T>* ret = NULL;
node = find(node);
if(node != NULL)
{
remove(dynamic_cast<BTreeNode<T>*>(node), ret);
m_queue.clear();
}
return ret;
}
測試技巧:直接打印已經刪除的子樹。
總結:
刪除操作將目標界定啊所在的子樹移除,必須完善處理父子結點的關系
void clear() // 將二叉樹中的所有節點清除(釋放堆中的結點)
1.清除操作功能定義
free(node) // 清除node為根結點的二叉樹,釋放二叉樹中的每個結點
// 清空樹的功能函數定義
void free(BTreeNode<T>* node)
{
if(node != NULL)
{
free(node->m_left);
free(node->m_right);
//cout << node->value << endl;
if(node->flag())
{
delete node;
}
}
}
void clear()
{
free(root());
this->m_root = NULL;
}測試技巧:可以在free函數中打印刪除的每一個結點
總結:
清除操作用于銷毀樹中的每個結點,銷毀時要判斷是否釋放對應的內存空間(工廠模式)。
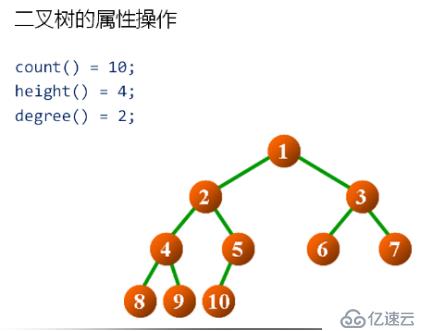
定義功能函數:cout(node) // 在node為根結點的二叉樹中遞歸統計結點數目
// 獲取樹的結點個數,遞歸實現
int count(BTreeNode<T>* node) const
{
int ret = 0;
if(node != NULL)
{
// 左子樹的結點個數 + 右子樹的結點個數 + 1(根結點)
ret = count(node->m_left) + count(node->m_right) + 1;
}
return ret;
}
int count() const
{
return count(root());
}定義功能函數:height(node) // 遞歸獲取node為根結點的二叉樹的高度
// 獲取樹的結點個數,遞歸實現
int height(BTreeNode<T>* node) const
{
int ret = 0;
if(node != NULL)
{
int hl = height(node->m_left);
int hr = height(node->m_right);
// 左右子樹高度的最大值 + 1(根結點)
ret = ((hl > hr) ? hl : hr) + 1;
}
return ret;
}
int height() const
{
return height(root());
}定義功能函數:degree(node) // 獲取node為根結點的二叉樹的度數
// 獲取二叉樹的度,遞歸實現
int degree(BTreeNode<T>* node) const
{
int ret = 0;
if(node != NULL)
{
/*
// 普通思路
int dl = degree(node->m_left); // 左子樹的度
int dr = degree(node->m_right); // 右子樹的度
ret = !!node->m_left + !!node->m_right; //根結點的度
if(dl > ret)
{
ret = dl;
}
else if(dr > ret)
{
ret = dr;
}
*/
/*
* 優化效率,二叉樹的最大度數為2,如果ret已經為2,則不需要繼續遍歷
ret = !!node->m_left + !!node->m_right; //根結點的度
if(ret < 2)
{
int dl = degree(node->m_left); // 左子樹的度
if(dl > ret)
{
ret = dl;
}
}
if(ret < 2)
{
int dr = degree(node->m_right); // 左子樹的度
if(dr > ret)
{
ret = dr;
}
}
*/
// 優化冗余代碼
ret = !!node->m_left + !!node->m_right; //根結點的度
BTreeNode<T>* child[] = {node->m_left, node->m_right};
for(int i=0; i<2 && ret<2; i++)
{
int d = degree(child[i]);
if(d > ret)
{
ret = d;
}
}
}
return ret;
}
int degree() const
{
return degree(root());
}二叉樹的遍歷是指從根結點出發,按照某種次序依次訪問二叉樹中的所有節點,使得每個結點被訪問一次。
思考:通用樹結構的層次遍歷算法是否可以用在二叉樹結構上?如果可以需要做什么改動?
不同之處在于二叉樹最多只有兩個孩子。
設計思路:
在樹中定義一個新游標(BTreeNode<T>*),遍歷開始將游標指向根結點(root()),獲取游標指向的數據元素,通過結點中的child成員移動游標;
提供一組遍歷相關的函數,按層次訪問樹中的數據元素。
層次遍歷算法:
原料:class LinkQueue<T>; 游標:LinkQueue<T>::front();
思想:
end() 判斷隊列是否為空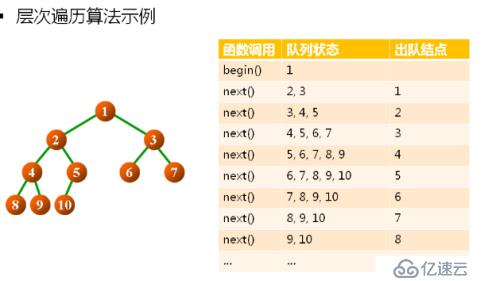
bool begin()
{
bool ret = (root() != NULL);
if(ret)
{
m_queue.clear();
m_queue.enqueue(root()); //把根結點壓入隊里
}
return ret;
}
bool end()
{
return (m_queue.length() == 0);
}
bool next()
{
bool ret = (m_queue.length() > 0);
if(ret)
{
BTreeNode<T>* node = m_queue.front();
m_queue.dequeue();
// 二叉樹的左右孩子入隊列
if(node->m_left != NULL)
{
m_queue.enqueue(node->m_left);
}
if(node->m_right != NULL)
{
m_queue.enqueue(node->m_right);
}
}
return ret;
}
// 獲取游標所執行的元素
T current()
{
if(!end())
{
return m_queue.front()->value;
}
else
{
THROW_EXCEPTION(InvalidOperationException, "invalid operation ...");
}
}使用示例:
for(bt.begin(); !bt.end(); bt.next())
{
cout << bt.current() << " ";
}
問題:二叉樹是否只有一種遍歷方式(層次遍歷)?
典型的二叉樹遍歷方式:
這里的先序、后序、中序指的的根結點的訪問次序
1.先序遍歷(Pre-Order Traversal)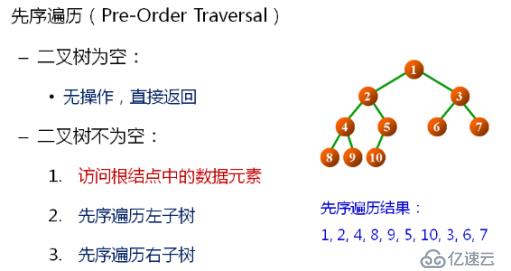
// 先序遍歷
void PreOrderTraversal(BTreeNode<T>* node, LinkQueue<BTreeNode<T>*>& queue)
{
if(node != NULL)
{
queue.enqueue(node);
PreOrderTraversal(node->m_left, queue);
PreOrderTraversal(node->m_right, queue);
}
}2.中序遍歷(In-Order TRaversal)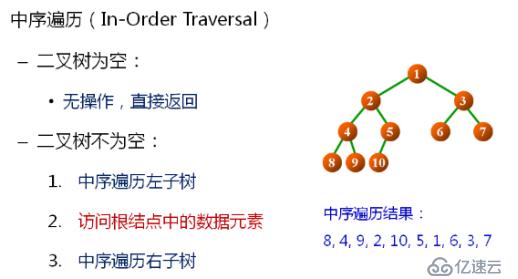
// 中序遍歷
void InOrderTraversal(BTreeNode<T>* node, LinkQueue<BTreeNode<T>*>& queue)
{
if(node != NULL)
{
InOrderTraversal(node->m_left, queue);
queue.enqueue(node);
InOrderTraversal(node->m_right, queue);
}
}3.后續遍歷(Post-Order Traversal)
// 后序遍歷
void PostOrderTraversal(BTreeNode<T>* node, LinkQueue<BTreeNode<T>*>& queue)
{
if(node != NULL)
{
PostOrderTraversal(node->m_left, queue);
PostOrderTraversal(node->m_right, queue);
queue.enqueue(node);
}
}4.層次遍歷(LevelOrder- Traversal)
// 層次遍歷
void LevelOrderTraversal(BTreeNode<T>* node,LinkQueue<BTreeNode<T>*>& queue)
{
if(node != NULL)
{
LinkQueue<BTreeNode<T>*> tmp; // 定義輔助隊列
tmp.enqueue(node); // 根結點入隊列
while(tmp.length()>0) // end
{
BTreeNode<T>* n = tmp.front();
if(n->m_left != NULL)
{
tmp.enqueue(n->m_left);
}
if(n->m_right != NULL)
{
tmp.enqueue(n->m_right);
}
tmp.dequeue(); //隊頭元素出隊列,并存入輸出隊列
queue.enqueue(n);
}
}
}思考:是否可以將二叉樹的典型遍歷方式算法集成到BTree中,如果可以,代碼需要做怎樣的改動?
設計要點:
1.不能與層次遍歷函數沖突,必須設計新的函數接口
2.算法執行完成后,能夠方便的獲得遍歷結果,遍歷結果能反映結點訪問的先后次序
函數接口設計:
SharedPoiner<Array<T>> traversal(BTTraversal order)
1.根據參數order選擇執行遍歷算法(先序、中序、后序)
2.返回值為堆中的數組對象(生命周期由智能指針管理)
3.數據元素的次序反映遍歷的先后次序
void traversal(BTTraversal order,LinkQueue<BTreeNode<T>*>& queue)
{
switch (order)
{
case PreOrder:
PreOrderTraversal(root(),queue);
break;
case InOrder:
InOrderTraversal(root(),queue);
break;
case PostOrder:
PostOrderTraversal(root(),queue);
break;
case LevelOrder:
LevelOrderTraversal(root(),queue);
break;
default:
THROW_EXCEPTION(InvaildParameterException,"Parameter order is invalid ...");
break;
}
}
SharedPointer<Array<T>> traversal(BTTraversal order)
{
DynamicArray<T>* ret = NULL;
LinkQueue<BTreeNode<T>*> queue; //保存執行二叉樹結點的指針
traversal(order, queue);
ret = new DynamicArray<T>(queue.length());
if(ret != NULL)
{
for(int i=0; i<ret->length(); i++,queue.dequeue())
{
//cout << queue.front()->value << endl;
ret->set(i, queue.front()->value);
}
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "no memory to create dynamic array...");
}
return ret;
}典型遍歷示例:
SharedPointer<Array<int>> sp = NULL;
sp = bt.traversal(PostOder);
for(int i=0; i<(*sp).length(); i++)
{
cout << (*sp)[i] << " ";
}總結:
1.二叉樹的典型遍歷都是以遞歸方式進行的;
2.BTree以不同的函數接口支持典型遍歷,防止與層次遍歷沖突;
克隆當前樹的一份拷貝,返回值為堆空間中的一顆新樹(與當前樹相等)。
SharedPointer<BTree<T>> clone() const
功能函數定義:clone(node)
遞歸克隆node為根結點的二叉樹(數據元素在對應位置相等)
BTreeNode<T>* clone(BTreeNode<T>* node) const
{
BTreeNode<T>* ret = NULL;
if(node != NULL)
{
ret = BTreeNode<T>::NewNode();
if(ret != NULL)
{
ret->value = node->value; // 克隆根結點
ret->m_left = clone(node->m_left); //遞歸克隆左子樹
ret->m_right = clone(node->m_right); //遞歸克隆右子樹
//連接父子關系
if(ret->m_left != NULL)
{
ret->m_left->m_parent = ret;
}
if(ret->m_right != NULL)
{
ret->m_right->m_parent = ret;
}
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "no memory to create new tree node...");
}
}
return ret;
}
SharedPointer<BTree<T>> clone() const
{
BTree<T>* ret = new BTree();
if(ret != NULL)
{
ret->m_root = clone(root());
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "no memory to create new tree...");
}
return ret;
}判斷兩顆二叉樹中的數據元素是否對應相等:
bool operater == (const BTree<T>& btree)
bool operater == (const BTree<T>& btree)
功能函數定義:equal(lh, rh)
遞歸判斷lh為根結點的二叉樹和rh為根結點的二叉樹是否相等。
bool equal(BTreeNode<T>* lh, BTreeNode<T>* rh)
{
bool ret = true;
if(lh == rh) // 自比較或者兩棵樹都為空
{
ret = true;
}
else if((lh != NULL) && (rh != NULL)) //參與比較的兩棵樹都不為空
{
// 遞歸比較根結點、左子樹、右子樹
ret = ((lh->value == rh->value) && (equal(lh->m_left, rh->m_left)) && equal(lh->m_right, rh->m_right));
}
else // 兩棵樹中有一顆為空
{
ret = false;
}
return ret;
}
bool operator == (const BTree<T>& btree)
{
return equal(root(), btree.root());
}
bool operator != (const BTree<T>& btree)
{
return !(*this == btree);
}將當前二叉樹與參數btree中的數據元素在對應的位置處相加,返回值(相加的結果)為堆空間中的一顆新二叉樹。
SharedPointer<BTree<T>> add(const BTree<T>& btree) const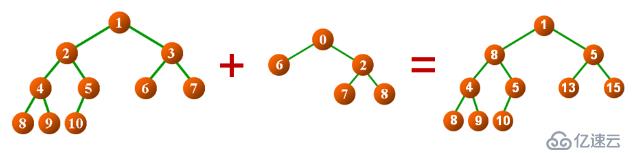
二叉樹相加操作功能函數定義:add(lh, rh),將lh為根節點的二叉樹與rh為根結點的二叉樹相加。
BTreeNode<T>* add(BTreeNode<T>* lh, BTreeNode<T>* rh) const
{
BTreeNode<T>* ret = NULL;
if((lh != NULL) && (rh == NULL)) // 二叉樹lh不為空
{
ret = clone(lh);
}
if((lh == NULL) && (rh != NULL)) // 二叉樹rh不為空
{
ret = clone(rh);
}
if((lh != NULL) && (rh != NULL)) // 二叉樹都不為空
{
ret = BTreeNode<T>::NewNode();
if(ret != NULL)
{
ret->value = lh->value + rh->value; // 根結點相加
ret->m_left = add(lh->m_left, rh->m_left); // 左子樹遞歸相加
ret->m_right = add(lh->m_right, rh->m_right); // 右子樹遞歸相加
//連接父子關系
if(ret->m_left != NULL)
{
ret->m_left->m_parent = ret;
}
if(ret->m_right != NULL)
{
ret->m_right->m_parent = ret;
}
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "no memory to create new tree node...");
}
}
return ret;
}
SharedPointer<BTree<T>> add(const BTree<T>& btree) const
{
BTree<T>* ret = new BTree();
if(ret != NULL)
{
ret->m_root = add(root(), btree.root());
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "no memory to create new node...");
}
return ret;
}1.什么是線索化二叉樹?
將二叉樹轉換為雙向鏈表的過程(非線性-->線性)的過程稱為線索化。
能夠反映某種二叉樹的遍歷次序(結點的先后訪問次序)
技巧:利用結點的right指針指向遍歷中的后繼結點,left指針指向前驅結點。
為什么要要進行線索化?
二叉樹的遍歷操作都采用遞歸進行(比較低效),如果需要經常遍歷,將二叉樹進行線索化后作為雙向鏈表存在,后續直接訪問雙向鏈表將提高效率。
2.如何對二叉樹進行線索化?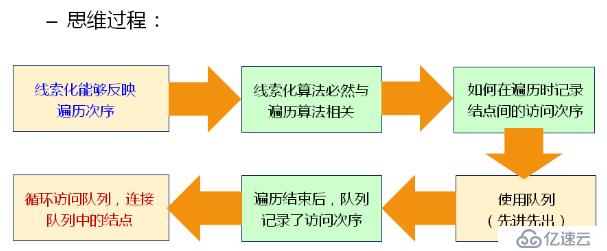
使用某種遍歷算法對二叉樹進行遍歷,在遍歷的同時將遍歷順序存儲到隊列,然后使用left和right指針連接隊列中的結點。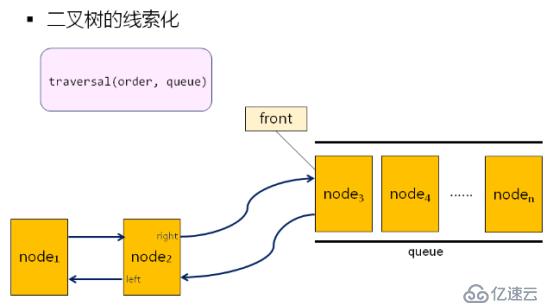
3.目標
新增共有函數BTreeNode<T>* thread(BTTraversal order)
4.層次遍歷實現
(1)將根結點壓入隊列
(2)訪問隊頭元素指向的二叉樹結點
(3)隊頭元素彈出,將隊頭元素的孩子壓入隊列
(4)判斷隊列是否為空(非空:執行2,空:結束)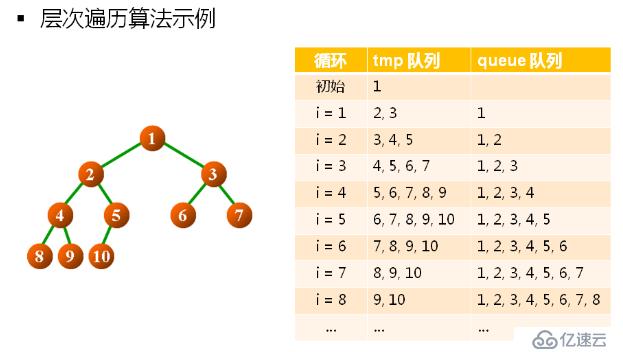

// 層次遍歷
void LevelOrderTraversal(BTreeNode<T>* node,LinkQueue<BTreeNode<T>*>& queue)
{
if(node != NULL)
{
LinkQueue<BTreeNode<T>*> tmp; // 定義輔助隊列
tmp.enqueue(node); // 根結點入隊列
while(tmp.length()>0) // end
{
BTreeNode<T>* n = tmp.front();
if(n->m_left != NULL)
{
tmp.enqueue(n->m_left);
}
if(n->m_right != NULL)
{
tmp.enqueue(n->m_right);
}
tmp.dequeue(); //隊頭元素出隊列,并存入輸出隊列
queue.enqueue(n);
}
}
}5.線索化實現
函數接口:BTreeNode<T>* thread(BTTraversal order)
(1)根據參數order選擇線索化的次序(先序、中序、后續、層次)
(2)連接線索化后的結點;
(3)返回線索化后指向鏈表首節點的指針,并將對應的二叉樹變為空樹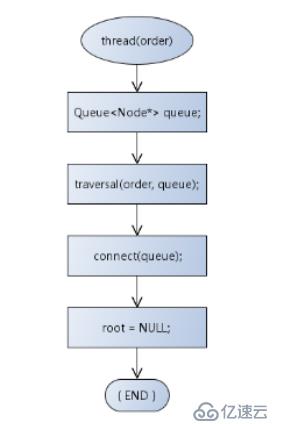
6.隊列中結點的連接
slider的right指針指向新的隊列頭部元素,隊頭元素的left指針指向slider,slider記錄隊頭元素,隊頭元素出隊列。
void traversal(BTTraversal order,LinkQueue<BTreeNode<T>*>& queue)
{
switch (order)
{
case PreOrder:
PreOrderTraversal(root(),queue);
break;
case InOrder:
InOrderTraversal(root(),queue);
break;
case PostOrder:
PostOrderTraversal(root(),queue);
break;
case LevelOrder:
LevelOrderTraversal(root(),queue);
break;
default:
THROW_EXCEPTION(InvaildParameterException,"Parameter order is invalid ...");
break;
}
}
BTreeNode<T>* connect(LinkQueue<BTreeNode<T>*>& queue)
{
BTreeNode<T>* ret = NULL;
if(queue.length() > 0)
{
//返回隊列的隊頭元素指向的結點作為雙向鏈表的首結點
ret = queue.front();
//創建一個游標結點,指向隊列隊頭
BTreeNode<T>* slider = queue.front();
//將隊頭元素出隊
queue.dequeue();
//雙向鏈表的首結點的前驅設置為空
ret->m_left = NULL;
while(queue.length() > 0)
{
//當前游標結點的后繼指向隊頭元素
slider->m_right = queue.front();
//當前隊頭元素的前驅指向當前游標結點
queue.front()->m_left = slider;
//將當前游標結點移動到隊頭元素
slider = queue.front();
//將當前隊頭元素出隊,繼續處理新的隊頭元素
queue.dequeue();
}
//雙向鏈表的尾結點的后繼為空
slider->m_right = NULL;
}
return ret;
}
BTreeNode<T>* thread(BTTraversal order)
{
BTreeNode<T>* ret = NULL;
LinkQueue<BTreeNode<T>*> queue;
traversal(order, queue); //遍歷二叉樹,并按遍歷次序將結點保存到隊列
ret = connect(queue); //連接隊列中的結點成為雙向鏈表
this->m_root = NULL; //將二叉樹的根節點置空
m_queue.clear(); //將游標遍歷的輔助隊列清空
//返回雙向鏈表的首結點
return ret;
}總結:
1.線索化是將二叉樹轉化為雙向鏈表的過程,線索華后結點間的先后次序符合某種遍歷次序;
2.線索化將破壞原二叉樹間的父子關系,同時線索化后二叉樹將不再管理結點中的生命周期(二叉樹已經不存在,只有雙向鏈表)。
要求:編寫一個函數用于刪除二叉樹中的所欲單度結點,結點刪除后,其唯一的子結點代替它的位置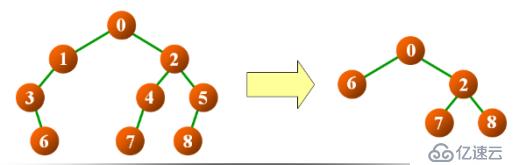
定義功能函數:delOdde(node) // 遞歸刪除node為根結點的二叉樹中的單度結點
template <typename T>
BTreeNode<T>* delOdd1(BTreeNode<T>* node)
{
BTreeNode<T>* ret = NULL;
if(node != NULL) //遞歸出口
{
// 判斷單度結點
if( ((node->m_left != NULL) && (node->m_right == NULL)) ||
((node->m_left == NULL) && (node->m_right != NULL)) )
{
BTreeNode<T>* parent = dynamic_cast<BTreeNode<T>*>(node->m_parent);
BTreeNode<T>* node_child = (node->m_left != NULL) ? node->m_left : node->m_right;
if(parent != NULL)
{
// 刪除單度結點,并使用唯一的子結點代替它的位置
BTreeNode<T>*& parent_child = (parent->m_left == node) ? parent->m_left : parent->m_right;
parent_child = node_child; // 處理指向子結點的指針
node_child->m_parent = parent; // 處理指向父結點指針
}
else
{
node_child->m_parent = NULL;
}
if(node->flag())
{
delete node; // 如果節點創建字堆空間,釋放內存
}
ret = delOdd1(node_child); // 最后刪除該單度結點
}
else // 非單度結點
{
delOdd1(node->m_left);
delOdd1(node->m_right);
ret = node;
}
}
return ret;
}定義功能函數:delOdde(node) // 遞歸刪除node為根結點的二叉樹中的單度結點,其中node為結點指針的引用
template <typename T>
void delOdd2(BTreeNode<T>*& node)
{
if(node != NULL) // 遞歸出口
{
// 判斷單度結點
if( ((node->m_left != NULL) && (node->m_right == NULL)) ||
((node->m_left == NULL) && (node->m_right != NULL)) )
{
// 刪除單度結點,并使用唯一的子結點代替它的位置
BTreeNode<T>* node_child = (node->m_left != NULL) ? node->m_left : node->m_right;
if(node->flag())
{
delete node;
}
node = node_child; // 因為沒有指向父結點的指針,所以只需要處理指向子結點的指針
delOdd2(node);
}
else // 非單度結點
{
delOdd2(node->m_left);
delOdd2(node->m_right);
}
}
}要求:編寫一個函數用于中序線索化二叉樹,不能使用其他的數據結構。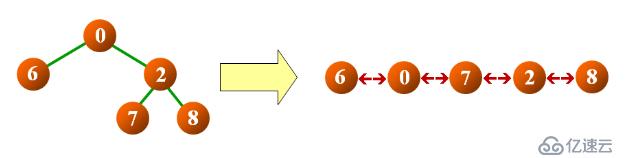
在中序遍歷的同時進行線索化
思路:使用輔助指針,在中序遍歷時指向當前結點的前驅結點,訪問當前結點時,連接與前驅結點的先后次序。
定義功能函數:inOrderThread(node,pre),其中node為根結點,也是中序遍歷訪問的結點,pre為中序遍歷時的前驅結點指針。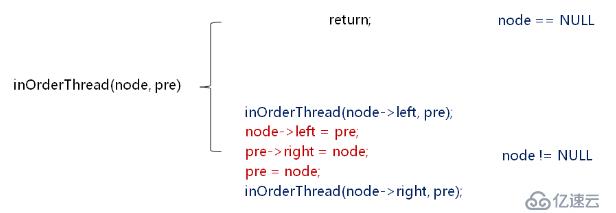
template <typename T>
// 其中node為根結點,也是中序遍歷訪問的結點,pre為中序遍歷時的前驅結點指針
void inOrderThread(BTreeNode<T>* node,BTreeNode<T>*& pre)
{
if(node != NULL)
{
inOrderThread(node->m_left,pre);
node->m_left = pre;
if(pre != NULL)
{
pre->m_right = node;
}
pre = node;
inOrderThread(node->m_right,pre);
}
}
template <typename T>
BTreeNode<T>* inOrderThread1(BTreeNode<T>* node)
{
BTreeNode<T>* pre = NULL;
inOrderThread(node,pre);
while((node != NULL) && (node->m_left != NULL))
{
node = node->m_left;
}
return node;
}中序遍歷的結點正好是結點的水平次序
思路:
1.使用輔助指針,指向轉換后雙向鏈表的頭節點和尾節點;
2.根結點與左右子樹轉為的雙向鏈表連接,稱為完整雙向鏈表。
定義功能函數:inOrderThread(node, head, tail):
Node為根結點,也是中序遍歷的訪問結點,head轉后成功后指向雙向鏈表的首節點,tail轉換成功后指向雙向鏈表的尾節點。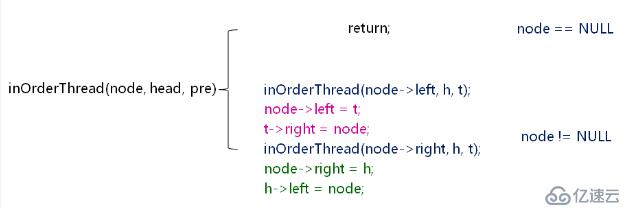
template <typename T>
// Node為根結點,也是中序遍歷的訪問結點,head轉換成功后指向雙向鏈表的首節點,tail轉換成功后指向雙向鏈表的尾節點
void inOrderThread(BTreeNode<T>* node,BTreeNode<T>*& head,BTreeNode<T>*& tail)
{
if(node != NULL)
{
BTreeNode<T>* h = NULL;
BTreeNode<T>* t = NULL;
inOrderThread(node->m_left,h,t);
node->m_left = t;
if(t != NULL)
{
t->m_right = node;
}
head = (h != NULL) ? h : node;
h = NULL;
t = NULL;
inOrderThread(node->m_right,h,t);
node->m_right = h;
if(h != NULL)
{
h->m_left = node;
}
tail = (t != NULL) ? t : node;
}
}
template <typename T>
BTreeNode<T>* inOrderThread2(BTreeNode<T>* node)
{
BTreeNode<T>* head = NULL;
BTreeNode<T>* tail = NULL;
inOrderThread(node,head,tail);
return head;
}免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。