您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本文將根據各種實用操作(遍歷、插入、刪除、排序、查找)并結合實例對常用數據結構進行性能分析。
數組是最常用的一種線性表,對于靜態的或者預先能確定大小的數據集合,采用數組進行存儲是最佳選擇。
數組的優點一是查找方便,利用下標即可立即定位到所需的數據節點;二是添加或刪除元素時不會產生內存碎片;三是不需要考慮數據節點指針的存儲。然而,數組作為一種靜態數據結構,存在內存使用率低、可擴展性差的缺點。無論數組中實際有多少元素,編譯器總會按照預先設定好的內存容量進行分配。如果超出邊界,則需要建立新的數組。
鏈表是另一種常用的線性表,一個鏈表就是一個由指針連接的數據鏈。每個數據節點由指針域和數據域構成,指針一般指向鏈表中的下一個節點,如果節點是鏈表中的最后一個,則指針為NULL。在雙向鏈表(Double Linked List)中,指針域還包括一個指向上一個數據節點的指針。在跳轉鏈表(Skip Linked List)中,指針域包含指向任意某個關聯向的指針。
template <typename T>
class LinkedNode
{
public:
LinkedNode(const T& e): pNext(NULL), pPrev(NULL)
{
data = e;
}
LinkedNode<T>* Next()const
{
return pNext;
}
LinkedNode<T>* Prev()const
{
return pPrev;
}
private:
T data;
LinkedNode<T>* pNext;// 指向下一個數據節點的指針
LinkedNode<T>* pPrev;// 指向上一個數據節點的指針
LinkedNode<T>* pConnection;// 指向關聯節點的指針
};與預先靜態分配好存儲空間的數組不同,鏈表的長度是可變的。只要內存空間足夠,程序就能持續為鏈表插入新的數據項。數組中所有的數據項都被存放在一段連續的存儲空間中,鏈表中的數據項會被隨機分配到內存的某個位置。
數組和鏈表有各自的優缺點,數組能夠方便定位到任何數據項,但擴展性較差;鏈表則無法提供快捷的數據項定位,但插入和刪除任意一個數據項都很簡單。當需要處理大規模的數據集合時,通常需要將數組和鏈表的優點結合。通過結合數組和鏈表的優點,哈希表能夠達到較好的擴展性和較高的訪問效率。
雖然每個開發者都可以構建自己的哈希表,但哈希表都有共同的基本結構,如下: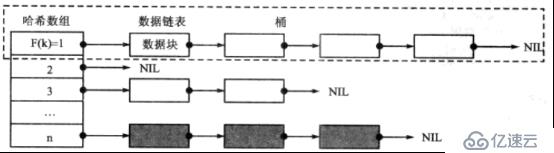
哈希數組中每個項都有指針指向一個小的鏈表,與某項相關的所有數據節點都會被存儲在鏈表中。當程序需要訪問某個數據節點時,不需要遍歷整個哈希表,而是先找到數組中的項,然后查詢子鏈表找到目標節點。每個子鏈表稱為一個桶(Bucket),如何定位一個存儲目標節點的桶,由數據節點的關鍵字域Key和哈希函數共同確定,雖然存在多種映射方法,但實現哈希函數最常用的方法還是除法映射。除法函數的形式如下:F(k) = k % D
k是數據節點的關鍵字,D是預先設計的常量,F(k)是桶的序號(等同于哈希數組中每個項的下標),哈希表實現如下:
// 數據節點定義
template <class E, class Key>
class LinkNode
{
public:
LinkNode(const E& e, const Key& k): pNext(NULL), pPrev(NULL)
{
data = e;
key = k;
}
void setNextNode(LinkNode<E, Key>* next)
{
pNext = next;
}
LinkNode<E, Key>* Next()const
{
return pNext;
}
void setPrevNode(LinkNode<E, Key>* prev)
{
pPrev = prev;
}
LinkNode<E, Key>* Prev()const
{
return pPrev;
}
E& getData()const
{
return data;
}
Key& getKey()const
{
return key;
}
private:
// 指針域
LinkNode<E, Key>* pNext;
LinkNode<E, Key>* pPrev;
// 數據域
E data;// 數據
Key key;//關鍵字
};
// 哈希表定義
template <class E, class Key>
class HashTable
{
private:
typedef LinkNode<E, Key>* LinkNodePtr;
LinkNodePtr* hashArray;// 哈希數組
int size;// 哈希數組大小
public:
HashTable(int n = 100);
~HashTable();
bool Insert(const E& data);
bool Delete(const Key& k);
bool Search(const Key& k, E& ret)const;
private:
LinkNodePtr searchNode()const;
// 哈希函數
int HashFunc(const Key& k)
{
return k % size;
}
};
// 哈希表的構造函數
template <class E, class Key>
HashTable<E, Key>::HashTable(int n)
{
size = n;
hashArray = new LinkNodePtr[size];
memset(hashArray, 0, size * sizeof(LinkNodePtr));
}
// 哈希表的析構函數S
template <class E, class Key>
HashTable<E, Key>::~HashTable()
{
for(int i = 0; i < size; i++)
{
if(hashArray[i] != NULL)
{
// 釋放每個桶的內存
LinkNodePtr p = hashArray[i];
while(p)
{
LinkNodePtr toDel = p;
p = p->Next();
delete toDel;
}
}
}
delete [] hashArray;
}分析代碼,哈希函數決定了一個哈希表的效率和性能。
當F(k)=k時,哈希表中的每個桶僅有一個節點,哈希表是一個一維數組,雖然每個數據節點的指針會造成一定的內存空間浪費,但查找效率最高(時間復雜度O(1))。
當F(k)=c時,哈希表所有的節點存放在一個桶中,哈希表退化為鏈表,同時還加上一個多余的、基本為空的數組,查找一個節點的時間效率為O(n),效率最低。
因此,構建一個理想的哈希表需要盡可能的使用讓數據節點分配更均勻的哈希函數,同時哈希表的數據結構也是影響其性能的一個重要因素。例如,桶的數量太少會造成巨大的鏈表,導致查找效率低下,太多的桶則會導致內存浪費。因此,在設計和實現哈希表前,需要分析數據節點的關鍵值,根據其分布來決定需要造多大的哈希數組和使用什么樣的哈希函數。
哈希表的實現中,數據節點的組織方式多種多樣,并不局限于鏈表,桶可以是一棵樹,也可以是一個哈希表。
二叉樹是一種常用數據結構,開發人員通常熟知二叉查找樹。在一棵二叉查找樹中,所有節點的左子節點的關鍵值都小于等于本身,而右子節點的關鍵值大于等于本身。由于平衡二叉查找樹與有序數組的折半查找算法原理相同,所以查詢效率要遠高于鏈表(O(Log2n)),而鏈表為O(n)。但由于樹中每個節點都要保存兩個指向子節點的指針,空間代價要遠高于單向鏈表和數組,并且樹中每個節點的內存分配是不連續的,導致內存碎片化。但二叉樹在插入、刪除以及查找等操作上的良好表現使其成為最常用的數據結構之一。二叉樹的鏈表實現如下:
template <class T>
class TreeNode
{
public:
TreeNode(const TreeNode& e): left(NULL), right(NULL)
{
data = e;
}
TreeNode<T>* Left()const
{
return left;
}
TreeNode<T>* Right()const
{
return right;
}
private:
T data;
TreeNode<T>* left;
TreeNode<T>* right;
};遍歷數組的操作很簡單,無論是順序還是逆序都可以遍歷數組,也可以任意位置開始遍歷數組。
跟蹤指針便能完成鏈表的遍歷:
LinkNode<E>* pNode = pFirst;
while(pNode)
{
pNode = pNode->Next();
// do something
}雙向鏈表可以支持順序和逆序遍歷,跳轉鏈表通過過濾某些無用節點可以實現快速遍歷。
如果預先知道所有節點的Key值,可以通過Key值和哈希函數找到每一個非空的桶,然后遍歷桶的鏈表。否則只能通過遍歷哈希數組的方式遍歷每個桶。
for(int i = 0; i < size; i++)
{
LinkNodePtr pNode = hashArray[i];
while(pNode) != NULL)
{
// do something
pNode = pNode->Next();
}
}遍歷二叉樹由三種方式:前序,中序,后序,三種遍歷方式的遞歸實現如下:
// 前序遍歷
template <class E>
void PreTraverse(TreeNode<E>* pNode)
{
if(pNode != NULL)
{
// do something
doSothing(pNode);
PreTraverse(pNode->Left());
PreTraverse(pNode->Right());
}
}
// 中序遍歷
template <class E>
void InTraverse(TreeNode<E>* pNode)
{
if(pNode != NULL)
{
InTraverse(pNode->Left());
// do something
doSothing(pNode);
InTraverse(pNode->Right());
}
}
// 后序遍歷
template <class E>
void PostTraverse(TreeNode<E>* pNode)
{
if(pNode != NULL)
{
PostTraverse(pNode->Left());
PostTraverse(pNode->Right());
// do something
doSothing(pNode);
}
}使用遞歸方式對二叉樹進行遍歷的缺點主要是隨著樹的深度增加,程序對函數棧空間的使用越來越多,由于棧空間的大小有限,遞歸方式遍歷可能會導致內存耗盡。解決辦法主要有兩個:一是使用非遞歸算法實現前序、中序、后序遍歷,即仿照遞歸算法執行時函數工作棧的變化狀況,建立一個棧對當前遍歷路徑上的節點進行記錄,根據棧頂元素是否存在左右節點的不同情況,決定下一步操作(將子節點入棧或當前節點退棧),從而完成二叉樹的遍歷;二是使用線索二叉樹,即根據遍歷規則,在每個葉子節點增加指向后續節點的指針。
由于數組中的所有數據節點都保存在連續的內存中,所以插入新的節點需要移動插入位置之后的所有節點以騰出空間,才能正確地將新節點復制到插入位置。如果恰好數組已滿,還需要重新建立一個新的容量更大的數組,將原數組的所有節點拷貝到新數組,因此數組的插入操作與其它數據結構相比,時間復雜度更高。
如果向一個未滿的數組插入節點,最好的情況是插入到數組的末尾,時間復雜度是O(1),最壞情況是插入到數組頭部,需要移動數組的所有節點,時間復雜度是O(n)。
如果向一個滿數組插入節點,通常做法是先創建一個更大的數組,然后將原數組的所有節點拷貝到新數組,同時插入新節點,最后刪除元數組,時間復雜度為O(n)。在刪除元數組之前,兩個數組必須并存一段時間,空間開銷較大。
在鏈表中插入一個新節點很簡單,對于單鏈表只需要修改插入位置之前節點的pNext指針使其指向本節點,然后將本節點的pNext指針指向下一個節點即可(對于鏈表頭不存在上一個節點,對于鏈表尾不存在下一個節點)。對于雙向鏈表和跳轉鏈表,需要修改相關節點的指針。鏈表的插入操作與長度無關,時間復雜度為O(1),當然鏈表的插入操作通常會伴隨鏈表插入節點位置的定位,需要一定時間。
在哈希表中插入一個節點需要完成兩部操作,定位桶并向鏈表插入節點。
template <class E, class Key>
bool HashTable<E, Key>::Insert(const E& data)
{
Key k = data;// 提取關鍵字
// 創建一個新節點
LinkNodePtr pNew = new LinkNodePtr(data, k);
int index = HashFunc(k);//定位桶
LinkNodePtr p = hashArray[index];
// 如果是空桶,直接插入
if(NULL == p)
{
hashArray[index] = pNew;
return true;
}
// 在表頭插入節點
hashArray[index] = pNew;
pNew->SetNextNode(p);
p->SetPrevNode(pNew);
return true;
}哈希表插入操作的時間復雜度為O(1),如果桶的鏈表是有序的,需要花時間定位鏈表中插入的位置,如果鏈表長度為M,則時間復雜度為O(M)。
二叉樹的結構直接影響插入操作的效率,對于平衡二叉查找樹,插入節點的時間復雜度為O(Log2N)。對于非平衡二叉樹,插入節點的時間復雜度比較高,在最壞情況下,非平衡二叉樹所有的left節點都為NULL,二叉樹退化為鏈表,插入節點新節點的時間復雜度為O(n)。
當節點數量很多時,對平衡二叉樹中進行插入操作的效率要遠高于非平衡二叉樹。工程開發中,通常避免非平衡二叉樹的出現,或是將非平衡二叉樹轉換為平衡二叉樹。簡單做法如下:
(1)中序遍歷非平衡二叉樹,在一個數組中保存所有的節點的指針。
(2)由于數組中所有元素都是有序排列的,可以使用折半查找遍歷數組,自上而下逐層構建平衡二叉樹。
從數組中刪除節點,如果需要數組沒有空洞,需要在刪除節點后將其后所有節點向前移動。最壞情況下(刪除首節點),時間復雜度為O(n),最好情況下(刪除尾節點),時間復雜度為O(1)。
在某些場合(如動態數組),當刪除完成后如果數組中存在大量空閑位置,則需要縮小數組,即創建一個較小的新數組,將原數組中所有節點拷貝到新數組,再將原數組刪除。因此,會導致較大的空間與時間開銷,應謹慎設置數組的大小,即要盡量避免內存空間的浪費也要減少數組的放大或縮小操作。通常,每當需要刪除數組中的某個節點時,并不將其真正刪除,而是在節點的位置設計一個標記位bDelete,將其設置為true,同時禁止其它程序使用本節點,待數組中需要刪除的節點達到一定閾值時,再統一刪除,避免多次移動節點操作,降低時間復雜度。
鏈表中刪除節點的操作,直接將被刪除節點的上一節點的指針指向被刪除節點的下一節點即可,刪除操作的時間復雜度是O(1)。
從哈希表中刪除一個節點的操作如下:首先通過哈希函數和鏈表遍歷(桶由鏈表實現)找到待刪除節點,然后刪除節點并重新設置前向和后向指針。如果被刪除節點是桶的首節點,則將桶的頭指針指向后續節點。
template <class E, class Key>
bool HashTable<E, Key>::Delete(const Key& k)
{
// 找到關鍵值匹配的節點
LinkNodePtr p = SearchNode(k);
if(NULL == p)
{
return false;
}
// 修改前向節點和后向節點的指針
LinkNodePtr pPrev = p->Prev();
if(pPrev)
{
LinkNodePtr pNext = p->Next();
if(pNext)
{
pNext->SetPrevNode(pPrev);
pPrev->SetNextNode(pNext);
}
else
{
// 如果前向節點為NULL,則當前節點p為首節點
// 修改哈希數組中的節點的指針,使其指向后向節點。
int index = HashFunc(k);
hashArray[index] = p->Next();
if(p->Next() != NULL)
{
p->Next()->SetPrevNode(NULL);
}
}
}
delete p;
return true;
}從二叉樹刪除一個節點需要根據情況討論:
(1)如果節點是葉子節點,直接刪除。
(2)如果刪除節點僅有一個子節點,則將子節點替換被刪除節點。
(3)如果刪除節點的左右子節點都存在,由于每個子節點都可能有自己的子樹,需要找到子樹中合適的節點,并將其立為新的根節點,并整合兩棵子樹,重新加入到原二叉樹。
數組的排序包括冒泡、選擇、插入等排序方法。
template <typename T>
void Swap(T& a, T& b)
{
T temp;
temp = a;
a = b;
b = temp;
}冒泡排序實現:
/**********************************************
* 排序方式:冒泡排序
* array:序列
* len:序列中元素個數
* min2max:按從小到大進行排序
* *******************************************/
template <typename T>
static void Bubble(T array[], int len, bool min2max = true)
{
bool exchange = true;
//遍歷所有元素
for(int i = 0; (i < len) && exchange; i++)
{
exchange = false;
//將尾部元素與前面的每個元素作比較交換
for(int j = len - 1; j > i; j--)
{
if(min2max?(array[j] < array[j-1]):(array[j] > array[j-1]))
{
//交換元素位置
Swap(array[j], array[j-1]);
exchange = true;
}
}
}
}冒泡排序的時間復雜度為O(n^2),冒泡排序是穩定的排序方法。
選擇排序實現:
/******************************************
* 排序方式:選擇排序
* array:序列
* len:序列中元素個數
* min2max:按從小到大進行排序
* ***************************************/
template <typename T>
void Select(T array[], int len, bool min2max = true)
{
for(int i = 0; i < len; i++)
{
int min = i;//從第i個元素開始
//對待排序的元素進行比較
for(int j = i + 1; j < len; j++)
{
//按排序的方式選擇比較方式
if(min2max?(array[min] > array[j]):(array[min] < array[j]))
{
min = j;
}
}
if(min != i)
{
//元素交換
Swap(array[i], array[min]);
}
}
}選擇排序的時間復雜度為O(n^2),選擇排序是不穩定的排序方法。
插入排序實現:
/******************************************
* 排序方式:選擇排序
* array:序列
* len:序列中元素個數
* min2max:按從小到大進行排序
* ***************************************/
template <typename T>
void Select(T array[], int len, bool min2max = true)
{
for(int i = 0; i < len; i++)
{
int min = i;//從第i個元素開始
//對待排序的元素進行比較
for(int j = i + 1; j < len; j++)
{
//按排序的方式選擇比較方式
if(min2max?(array[min] > array[j]):(array[min] < array[j]))
{
min = j;
}
}
if(min != i)
{
//元素交換
Swap(array[i], array[min]);
}
}
}插入排序的時間復雜度為O(n^2),插入排序是穩定的排序方法。
雖然鏈表在插入和刪除操作上性能優越,但排序復雜度卻很高,尤其是單向鏈表。由于鏈表中訪問某個節點需要依賴其它節點,不能根據下標直接定位到任意一項,因此節點定位的時間復雜度為O(N),排序效率低下。
工程開發中,可以使用數組鏈表,當需要排序時構造一個數組,存放鏈表中每個節點的指針。在排序過程中通過數組定位每個節點,并實現節點的交換。
鏈表數組為直接訪問鏈表的節點提供了便利,但是使用空間換時間的方法,如果希望得到一個有序鏈表,最好是在構建鏈表時將每個節點插入到合適的位置。
由于采用哈希函數訪問每個桶,因此哈希表中對哈希數組排序毫無意義,但具體節點的定位需要通過查詢每個桶鏈表完成(桶由鏈表實現),將桶的鏈表排序可以提高節點的查詢效率。
對于二叉查找樹,其本身是有序的,中序遍歷可以得到二叉查找樹有序的節點輸出。對于未排序的二叉樹,所有節點被隨機組織,定位節點的時間復雜度為O(N)。
數組的最大優點是可以通過下標任意的訪問節點,而不需要借助指針、索引或遍歷,時間復雜度為O(1)。對于下標未知的情況查找節點,則只能遍歷數組,時間復雜度為O(N)。對于有序數組,最好的查找算法是二分查找法。
template <class E>
int BinSearch(E array[], const E& value, int start, int end)
{
if(end - start < 0)
{
return INVALID_INPUT;
}
if(value == array[start])
{
return start;
}
if(value == array[end])
{
return end;
}
while(end > start + 1)
{
int temp = (end + start) / 2;
if(value == array[temp])
{
return temp;
}
if(array[temp] < value)
{
start = temp;
}
else
{
end = temp;
}
}
return -1;
}折半查找的時間復雜度是O(Log2N),與二叉樹查詢效率相同。
對于亂序數組,只能通過遍歷方法查找節點,工程開發中通常設置一個標識變量保存更新節點的下標,執行查詢時從標識變量標記的下標開始遍歷數組,執行效率比從頭開始要高。
對于單向鏈表,最差情況下需要遍歷整個鏈表才能找到需要的節點,時間復雜度為O(N)。
對于有序鏈表,可以預先獲取某些節點的數據,可以選擇與目標數據最接近的一個節點查找,效率取決于已知節點在鏈表中的分布,對于雙向有序鏈表效率會更高,如果正中節點已知,則查詢的時間復雜度為O(N/2)。
對于跳轉鏈表,如果預先能夠根據鏈表中節點之間的關系建立指針關聯,查詢效率將大大提高。
哈希表中查詢的效率與桶的數據結構有關。桶由鏈表實現,則查詢效率和鏈表長度有關,時間復雜度為O(M)。查找算法實現如下:
template <class E, class Key>
bool HashTable<E, Key>::SearchNode(const Key& k)const
{
int index = HashFunc(k);
// 空桶,直接返回
if(NULL == hashArray[index])
return NULL;
// 遍歷桶的鏈表,如果由匹配節點,直接返回。
LinkNodePtr p = hashArray[index];
while(p)
{
if(k == p->GetKey())
return p;
p = p->Next();
}
}在二叉樹中查找節點與樹的形狀有關。對于平衡二叉樹,查找效率為O(Log2N);對于完全不平衡的二叉樹,查找效率為O(N);
工程開發中,通常需要構建盡量平衡的二叉樹以提高查詢效率,但平衡二叉樹受插入、刪除操作影響很大,插入或刪除節點后需要調整二叉樹的結構,通常,當二叉樹的插入、刪除操作很多時,不需要在每次插入、刪除操作后都調整平衡度,而是在密集的查詢操作前統一調整一次。
工程開發中,數組是常用數據結構,如果在編譯時就知道數組所有的維數,則可以靜態定義數組。靜態定義數組后,數組在內存中占據的空間大小和位置是固定的,如果定義的是全局數組,編譯器將在靜態數據區為數組分配空間,如果是局部數組,編譯器將在棧上為數組分配空間。但如果預先無法知道數組的維數,程序只有在運行時才知道需要分配多大的數組,此時C++編譯器可以在堆上為數組動態分配空間。
動態數組的優點如下:
(1)可分配空間較大。棧的大小都有限制,Linux系統可以使用ulimit -s查看,通常為8K。開發者雖然可以設置,但由于需要保證程序運行效率,通常不宜太大。堆空間的通常可供分配內存比較大,達到GB級別。
(2)使用靈活。開發人員可以根據實際需要決定數組的大小和維數。
動態數組的缺點如下:
(1)空間分配效率比靜態數組低。靜態數組一般由棧分配空間,動態數組一般由堆分配空間。棧是機器系統提供的數據結構,計算機會在底層為棧提供支持,即分配專門的寄存器存放棧的地址,壓棧和出棧都有專門的機器指令執行,因而棧的效率比較高。堆由C++函數庫提供,其內存分配機制比棧要復雜得多,為了分配一塊內存,庫函數會按照一定的算法在堆內存內搜索可用的足夠大小的空間,如果發現空間不夠,將調用內核方法去增加程序數據段的存儲空間,從而程序就有機會分配足夠大的內存。因此堆的效率要比棧低。
(2)容易造成內存泄露。動態內存需要開發人員手工分配和釋放內存,容易由于開發人員的疏忽造成內存泄露。
在實時視頻系統中,視頻服務器承擔視頻數據的緩存和轉發工作。一般,服務器為每臺攝像機開辟一定大小且獨立的緩存區。視頻幀被寫入此緩存區后,服務器在某一時刻再將其讀出,并向客戶端轉發。視頻幀的轉發是臨時的,由于緩存區大小有限而視頻數據源源不斷,所以一幀數據在被寫入過后,過一段時間并會被新來的視頻幀所覆蓋。視頻幀的緩存時間由緩存區和視頻幀的長度決定。
由于視頻幀數據量巨大,而一臺服務器通常需要支持幾十臺甚至數百臺攝像機,緩存結構的設計是系統的重要部分。一方面,如果預先分配固定數量的內存,運行時不再增加、刪除,則服務器只能支持一定數量的攝像機,靈活性小;另一方面,由于視頻服務器程序在啟動時將占據一大塊內存,將導致系統整體性能下降,因此考慮使用動態數組實現視頻緩存。
首先,服務器中為每臺攝像機分配一個一定大小的緩存塊,由類CamBlock實現。每個CamBlock對象中有兩個動態數組,分別存放視頻數據的_data和存放視頻幀索引信息的_frameIndex。每當程序在內存中緩存(讀取)一個視頻幀時,對應的CamBlock對象將根據視頻幀索引表_frameIndex找到視頻幀在_data中的存放位置,然后將數據寫入或讀出。_data是一個循環隊列,一般根據FIFO進行讀取,即如果有新幀進入隊列,程序會在_data中最近寫入幀的末尾開始復制,如果超出數組長度,則從頭覆蓋。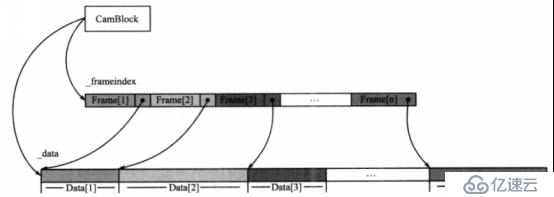
// 視頻幀的數據結構
typedef struct
{
unsigned short idCamera;// 攝像機ID
unsigned long length;// 數據長度
unsigned short width;// 圖像寬度
unsigned short height;// 圖像高度
unsigned char* data; // 圖像數據地址
} Frame;
// 單臺攝像機的緩存塊數據結構
class CamBlock
{
public:
CamBlock(int id, unsigned long len, unsigned short numFrames):
_data(NULL), _length(0), _idCamera(-1), _numFrames(0)
{
// 確保緩存區大小不超過閾值
if(len > MAX_LENGTH || numFrames > MAX_FRAMES)
{
throw;
}
try
{
// 為幀索引表分配空間
_frameIndex = new Frame[numFrames];
// 為攝像機分配指定大小的內存
_data = new unsigned char[len];
}
catch(...)
{
throw;
}
memset(this, 0, len);
_length = len;
_idCamera = id;
_numFrames = numFrames;
}
~CamBlcok()
{
delete [] _frameIndex;
delete [] _data;
}
// 根據索引表將視頻幀存入緩存
bool SaveFrame(const Frame* frame);
// 根據索引表定位到某一幀,讀取
bool ReadFrame(Frame* frame);
private:
Frame* _frameIndex;// 幀索引表
unsigned char* _data;//存放圖像數據的緩存區
unsigned long _length;// 緩存區大小
unsigned short _idCamera;// 攝像機ID
unsigned short _numFrames;//可存放幀的數量
unsigned long _lastFrameIndex;//最后一幀的位置
};為了管理每臺攝像機獨立的內存塊,快速定位到任意一臺攝像機的緩存,甚至任意一幀,需要建立索引表CameraArray來管理所有的CamBlock對象。
class CameraArray
{
typedef CamBlock BlockPtr;
BlockPtr* cameraBufs;// 攝像機視頻緩存
unsigned short cameraNum;// 當前已經連接的攝像機臺數
unsigned short maxNum;//cameraBufs容量
unsigned short increaseNum;//cameraBufs的增量
public:
CameraArray(unsigned short max, unsigned short inc);
~CameraArray();
// 插入一臺攝像機
CamBlock* InsertBlock(unsigned short idCam, unsigned long size, unsigned short numFrames);
// 刪除一臺攝像機
bool RemoveBlock(unsigned short idCam);
private:
// 根據攝像機ID返回其在數組的索引
unsigned short GetPosition(unsigned short idCam);
};
CameraArray::CameraArray(unsigned short max, unsigned short inc):
cameraBufs(NULL), cameraNum(0), maxNum(0), increaseNum(0)
{
// 如果參數越界,拋出異常
if(max > MAX_CAMERAS || inc > MAX_INCREMENTS)
throw;
try
{
cameraBufs = new BlockPtr[max];
}
catch(...)
{
throw;
}
maxNum = max;
increaseNum = inc;
}
CameraArray::~CameraArray()
{
for(int i = 0; i < cameraNum; i++)
{
delete cameraBufs[i];
}
delete [] cameraBufs;
}通常,會為每個攝像機安排一個整型的ID,在CameraArray中,程序按照ID遞增的順序排列每個攝像機的CamBlock對象以方便查詢。當一個新的攝像機接入系統時,程序會根據它的ID在CameraArray中找到一個合適的位置,然后利用相應位置的指針創建一個新的CamBlock對象;當某個攝像機斷開連接,程序也會根據它的ID,找到對應的CamBlock緩存塊,并將其刪除。
CamBlock* CameraArray::InsertBlock(unsigned short idCam, unsigned long size,
unsigned short numFrames)
{
// 在數組中找到合適的插入位置
int pos = GetPosition(idCam);
// 如果已經達到數組邊界,需要擴大數組
if(cameraNum == maxNum)
{
// 定義新的數組指針,指定其維數
BlockPtr* newBufs = NULL;
try
{
BlockPtr* newBufs = new BlockPtr[maxNum + increaseNum];
}
catch(...)
{
throw;
}
// 將原數組內容拷貝到新數組
memcpy(newBufs, cameraBufs, maxNum * sizeof(BlockPtr));
// 釋放原數組的內存
delete [] cameraBufs;
maxNum += increaseNum;
// 更新數組指針
cameraBufs = newBufs;
}
if(pos != cameraNum)
{
// 在數組中插入一個塊,需要將其后所有指針位置后移
memmov(cameraBufs + pos + 1, cameraBufs + pos, (cameraNum - pos) * sizeof(BlockPtr));
}
++cameraNum;
CamBlock* newBlock = new CamBlock(idCam, size, numFrames);
cameraBufs[pos] = newBlock;
return cameraBufs[pos];
}如果接入系統的攝像機數量超出了最初創建CameraArray的設計容量,則考慮到系統的可擴展性,只要硬件條件允許,需要增加cameraBufs的長度。
bool CameraArray::RemoveBlock(unsigned short idCam)
{
if(cameraNum < 1)
return false;
// 在數組中找到要刪除的攝像機的緩存區的位置
int pos = GetPosition(idCam);
cameraNum--;
BlockPtr deleteBlock = cameraBufs[pos];
delete deleteBlock;
if(pos != cameraNum)
{
// 將pos后所有指針位置前移
memmov(cameraBufs + pos, cameraBufs + pos + 1, (cameraNum - pos) * sizeof(BlockPtr));
}
// 如果數組中有過多空閑的位置,進行釋放
if(maxNum - cameraNum > increaseNum)
{
// 重新計算數組的長度
unsigned short len = (cameraNum / increaseNum + 1) * increaseNum;
// 定義新的數組指針
BlockPtr* newBufs = NULL;
try
{
newBufs = new BlockPtr[len];
}
catch(...)
{
throw;
}
// 將原數組的數據拷貝到新的數組
memcpy(newBufs, cameraBufs, cameraNum * sizeof(BlockPtr));
delete cameraBufs;
cameraBufs = newBufs;
maxNum = len;
}
return true;
}如果刪除一臺攝像機時,發現數組空間有過多空閑空間,則需要釋放相應空閑空間。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。