怎么使用Python實現漢諾塔問題

今天小編給大家分享一下怎么使用Python實現漢諾塔問題的相關知識點，內容詳細，邏輯清晰，相信大部分人都還太了解這方面的知識，所以分享這篇文章給大家參考一下，希望大家閱讀完這篇文章后有所收獲，下面我們一起來了解一下吧。

前言

漢諾塔問題是一個經典的問題。漢諾塔（Hanoi Tower），又稱河內塔，源于印度一個古老傳說。大梵天創造世界的時候做了三根金剛石柱子，在一根柱子上從下往上按照大小順序摞著64片黃金圓盤。大梵天命令婆羅門把圓盤從下面開始按大小順序重新擺放在另一根柱子上。并且規定，任何時候，在小圓盤上都不能放大圓盤，且在三根柱子之間一次只能移動一個圓盤。問應該如何操作？

1.先談一下什么是遞歸？

我自己的理解就是：將自身的問題不斷減小規模，直到減小到無法減小為止。（到達遞歸結束條件）然后從小問題開始解決，小問題逐個解決之后，大問題也就迎刃而解了（遞歸回來了）

2.簡而言之就是：

原問題不斷減小為規模更小的原問題，然后小規模的原問題解決了，從而解決原來的大問題！

3.過程為：

減小規模、從小解決、遞歸回來、解決原問題！！！

4.遞歸的關鍵是：

（1）有遞歸結束條件。

（2）不斷調用自身，減小問題規模，向遞歸結束條件靠攏。

漢諾塔問題

1.問題描述

有三根柱子，分別名為A,B,C。初始時，在柱子A上有n個圓盤，他們從下到上，盤子的大小是從大到小。在移動和擺放的過程中，小盤子必須在大盤子上面。 在保證規則的情況下，將柱子A上的所有盤子，移動到柱子C，移動中可以借助柱子B，但是得保證移動過程中小盤子必須得在大盤子上！！！ 請打印出移動過程？

2.問題分析 遞歸的過程：

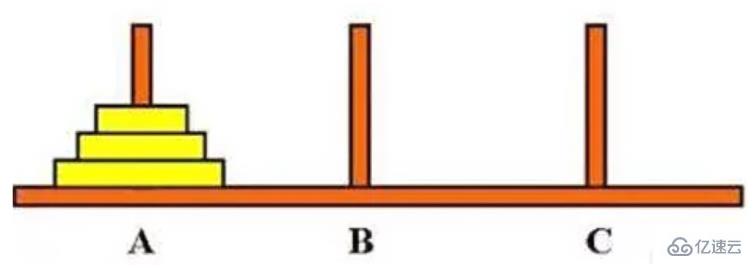
（1）將最上面的n-1個盤子，從A借助C移動到B

（2）將最下面的一個盤子，從A移動到C

（3）將最上面的n-1個盤子，從B借助A移動到C

遞歸的結束條件：

問題規模變成盤子數為0時，因為當盤子數為0時就不需要移動了！！！

3.代碼（Python）

# coding:utf-8

"""
    n為初始時A柱上的盤子數
    a為起始盤子所在的柱子
    b為中轉柱子
    c為目的地柱子
"""


def hanoi(n, a, b, c):
    if n > 0:
        hanoi(n-1, a, c, b)
        print("盤子從%s移動到%s" % (a, c))
        hanoi(n-1, b, a, c)



hanoi(3, "A", "B", "C")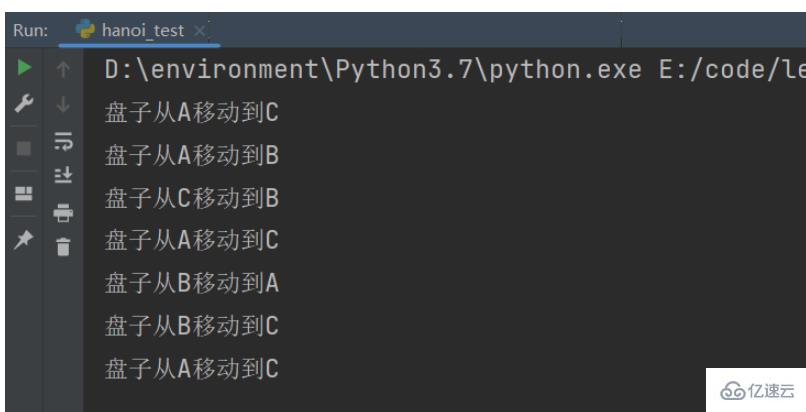

4.結果展示

以上就是“怎么使用Python實現漢諾塔問題”這篇文章的所有內容，感謝各位的閱讀！相信大家閱讀完這篇文章都有很大的收獲，小編每天都會為大家更新不同的知識，如果還想學習更多的知識，請關注億速云行業資訊頻道。