您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“java并查集怎么實現”,在日常操作中,相信很多人在java并查集怎么實現問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”java并查集怎么實現”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
并查集:一種樹型數據結構,用于解決一些不相交集合的合并及查詢問題。例如:有n個村莊,查詢2個村莊之間是否有連接的路,連接2個村莊
兩大核心:
查找 (Find) : 查找元素所在的集合
合并 (Union) : 將兩個元素所在集合合并為一個集合
并查集有兩種常見的實現思路
快查(Quick Find)
查找(Find)的時間復雜度:O(1)
合并(Union)的時間復雜度:O(n)
快并(Quick Union)
查找(Find)的時間復雜度:O(logn)可以優化至O(a(n))a(n)< 5
合并(Union)的時間復雜度:O(logn)可以優化至O(a(n))a(n)< 5
使用數組實現樹型結構,數組下標為元素,數組存儲的值為父節點的值
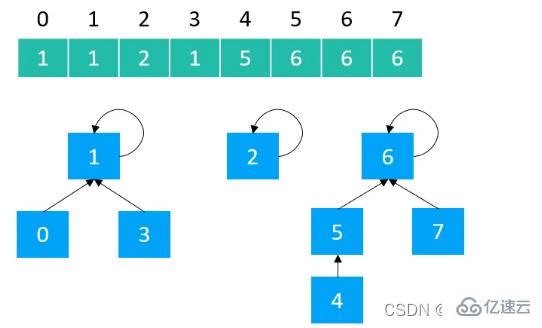
創建抽象類Union Find
public abstract class UnionFind {
int[] parents;
/**
* 初始化并查集
* @param capacity
*/
public UnionFind(int capacity){
if(capacity < 0) {
throw new IllegalArgumentException("capacity must be >=0");
}
//初始時每一個元素父節點(根結點)是自己
parents = new int[capacity];
for(int i = 0; i < parents.length;i++) {
parents[i] = i;
}
}
/**
* 檢查v1 v2 是否屬于同一個集合
*/
public boolean isSame(int v1,int v2) {
return find(v1) == find(v2);
}
/**
* 查找v所屬的集合 (根節點)
*/
public abstract int find(int v);
/**
* 合并v1 v2 所屬的集合
*/
public abstract void union(int v1, int v2);
// 范圍檢查
public void rangeCheck(int v) {
if(v<0 || v > parents.length)
throw new IllegalArgumentException("v is out of capacity");
}
}以Quick Find實現的并查集,樹的高度最高為2,每個節點的父節點就是根節點
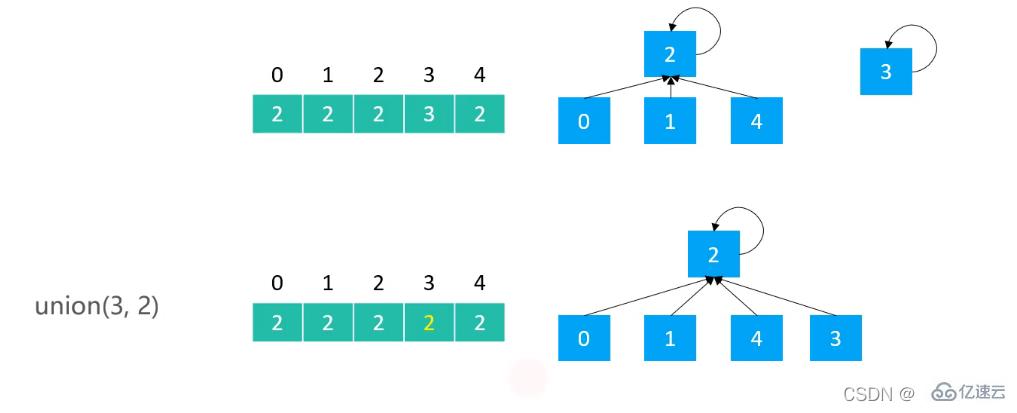
public class UnionFind_QF extends UnionFind {
public UnionFind_QF(int capacity) {
super(capacity);
}
// 查
@Override
public int find(int v) {
rangeCheck(v);
return parents[v];
}
// 并 將v1所在集合并到v2所在集合上
@Override
public void union(int v1, int v2) {
// 查找v1 v2 的父(根)節點
int p1= find(v1);
int p2 = find(v2);
if(p1 == p2) return;
//將所有以v1的根節點為根節點的元素全部并到v2所在集合上 即父節點改為v2的父節點
for(int i = 0; i< parents.length; i++) {
if(parents[i] == p1) {
parents[i] = p2;
}
}
}
}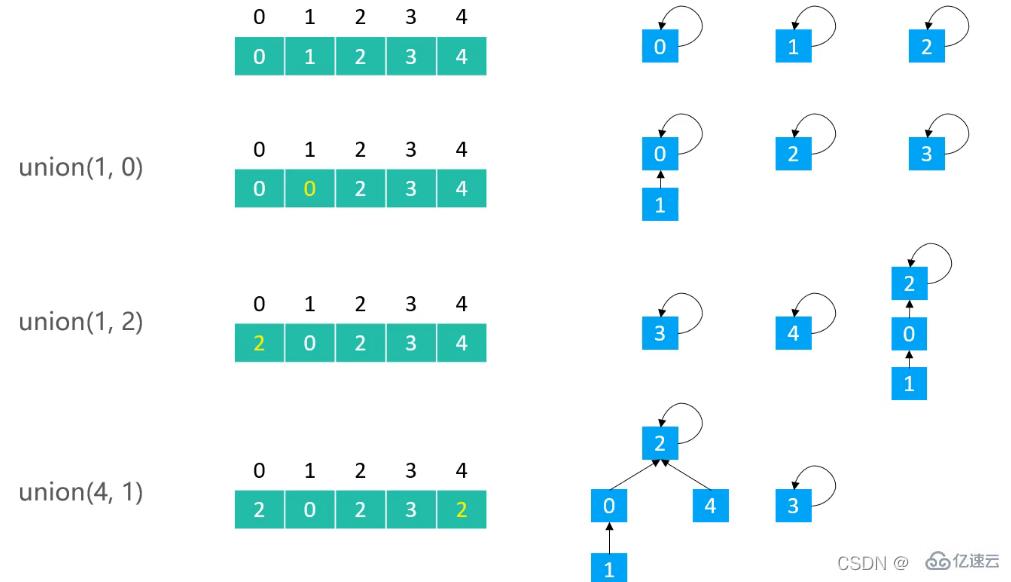
public class UnionFind_QU extends UnionFind {
public UnionFind_QU(int capacity) {
super(capacity);
}
//查某一個元素的根節點
@Override
public int find(int v) {
//檢查下標是否越界
rangeCheck(v);
// 一直循環查找節點的根節點
while (v != parents[v]) {
v = parents[v];
}
return v;
}
//V1 并到 v2 中
@Override
public void union(int v1, int v2) {
int p1 = find(v1);
int p2 = find(v2);
if(p1 == p2) return;
//將v1 根節點 的 父節點 修改為 v2的根結點 完成合并
parents[p1] = p2;
}
}并查集常用快并來實現,但是快并有時會出現樹不平衡的情況
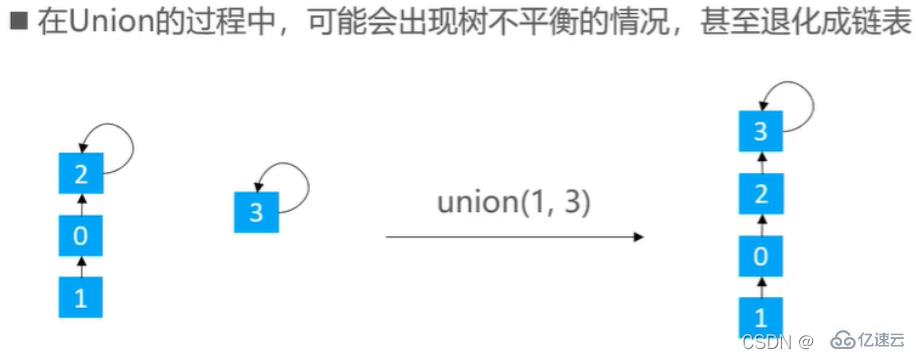
有兩種優化思路:rank優化,size優化
核心思想:元素少的樹 嫁接到 元素多的樹
public class UniondFind_QU_S extends UnionFind{
// 創建sizes 數組記錄 以元素(下標)為根結點的元素(節點)個數
private int[] sizes;
public UniondFind_QU_S(int capacity) {
super(capacity);
sizes = new int[capacity];
//初始都為 1
for(int i = 0;i < sizes.length;i++) {
sizes[i] = 1;
}
}
@Override
public int find(int v) {
rangeCheck(v);
while (v != parents[v]) {
v = parents[v];
}
return v;
}
@Override
public void union(int v1, int v2) {
int p1 = find(v1);
int p2 = find(v2);
if(p1 == p2) return;
//如果以p1為根結點的元素個數 小于 以p2為根結點的元素個數 p1并到p2上,并且更新p2為根結點的元素個數
if(sizes[p1] < sizes[p2]) {
parents[p1] = p2;
sizes[p2] += sizes[p1];
// 反之 則p2 并到 p1 上,更新p1為根結點的元素個數
}else {
parents[p2] = p1;
sizes[p1] += sizes[p2];
}
}
}基于size優化還有可能會導致樹不平衡
核心思想:矮的樹 嫁接到 高的樹
public class UnionFind_QU_R extends UnionFind_QU {
// 創建rank數組 ranks[i] 代表以i為根節點的樹的高度
private int[] ranks;
public UnionFind_QU_R(int capacity) {
super(capacity);
ranks = new int[capacity];
for(int i = 0;i < ranks.length;i++) {
ranks[i] = 1;
}
}
public void union(int v1, int v2) {
int p1 = find(v1);
int p2 = find(v2);
if(p1 == p2) return;
// p1 并到 p2 上 p2為根 樹的高度不變
if(ranks[p1] < ranks[p2]) {
parents[p1] = p2;
// p2 并到 p1 上 p1為根 樹的高度不變
} else if(ranks[p1] > ranks[p2]) {
parents[p2] = p1;
}else {
// 高度相同 p1 并到 p2上,p2為根 樹的高度+1
parents[p1] = p2;
ranks[p2] += 1;
}
}
}基于rank優化,隨著Union次數的增多,樹的高度依然會越來越高 導致find操作變慢
有三種思路可以繼續優化 :路徑壓縮、路徑分裂、路徑減半
在find時使路徑上的所有節點都指向根節點,從而降低樹的高度
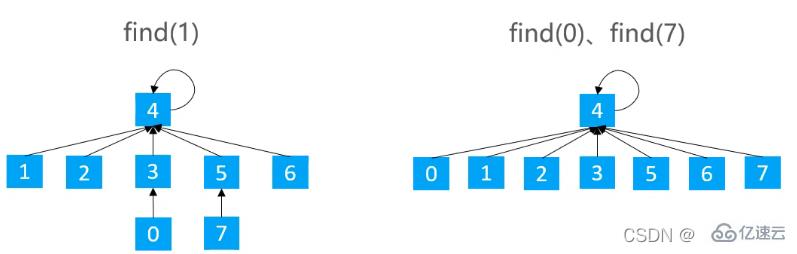
/**
* Quick Union -基于rank的優化 -路徑壓縮
*
*/
public class UnionFind_QU_R_PC extends UnionFind_QU_R {
public UnionFind_QU_R_PC(int capacity) {
super(capacity);
}
@Override
public int find(int v) {
rangeCheck(v);
if(parents[v] != v) {
//遞歸 使得從當前v 到根節點 之間的 所有節點的 父節點都改為根節點
parents[v] = find(parents[v]);
}
return parents[v];
}
}雖然能降低樹的高度,但是實現成本稍高
使路徑上的每個節點都指向其祖父節點

/**
* Quick Union -基于rank的優化 -路徑分裂
*
*/
public class UnionFind_QU_R_PS extends UnionFind_QU_R {
public UnionFind_QU_R_PS(int capacity) {
super(capacity);
}
@Override
public int find(int v) {
rangeCheck(v);
while(v != parents[v]) {
int p = parents[v];
parents[v] = parents[parents[v]];
v = p;
}
return v;
}
}使路徑上每隔一個節點就指向其祖父節點
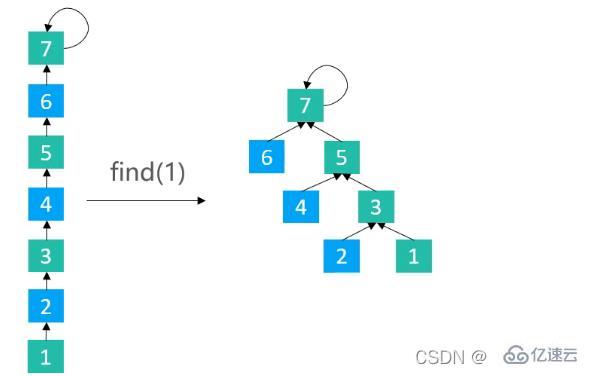
/**
* Quick Union -基于rank的優化 -路徑減半
*
*/
public class UnionFind_QU_R_PH extends UnionFind_QU_R {
public UnionFind_QU_R_PH(int capacity) {
super(capacity);
}
public int find(int v) {
rangeCheck(v);
while(v != parents[v]) {
parents[v] = parents[parents[v]];
v = parents[v];
}
return v;
}
}使用Quick Union + 基于rank的優化 + 路徑分裂 或 路徑減半
可以保證每個操作的均攤時間復雜度為O(a(n)) , a(n) < 5
到此,關于“java并查集怎么實現”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。