您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹了Java Morris遍歷算法及在二叉樹中應用的方法是什么的相關知識,內容詳細易懂,操作簡單快捷,具有一定借鑒價值,相信大家閱讀完這篇Java Morris遍歷算法及在二叉樹中應用的方法是什么文章都會有所收獲,下面我們一起來看看吧。
Morris遍歷是一種用于二叉樹遍歷的算法,它可以在不使用棧或隊列的情況下實現中序遍歷。該算法的時間復雜度為O(n),空間復雜度為O(1)。
Morris遍歷的基本思想是,利用葉子節點的空指針來存儲臨時信息,以達到節省空間的目的。具體來說,對于當前遍歷到的節點,如果它有左子節點,就找到左子樹中最右邊的節點,將其右子節點指向當前節點,然后將當前節點更新為其左子節點。如果它沒有左子節點,就輸出當前節點的值,并將當前節點更新為其右子節點。重復以上步驟,直到遍歷完整棵樹。
Morris遍歷的優點是空間復雜度低O(1),但它的缺點是會改變原來的二叉樹結構,因此需要在遍歷完后還原二叉樹。此外,該算法可能會比遞歸或使用棧的算法稍微慢一些。
二叉樹的線索化,主要是利用了葉子結點中的空指針域,存放了在某種遍歷順序下的前驅或者后續結點,從而達到了線索二叉樹的目的
例如,下圖中序遍歷結果展示如下,根據中序遍歷對空指針域進行線索化
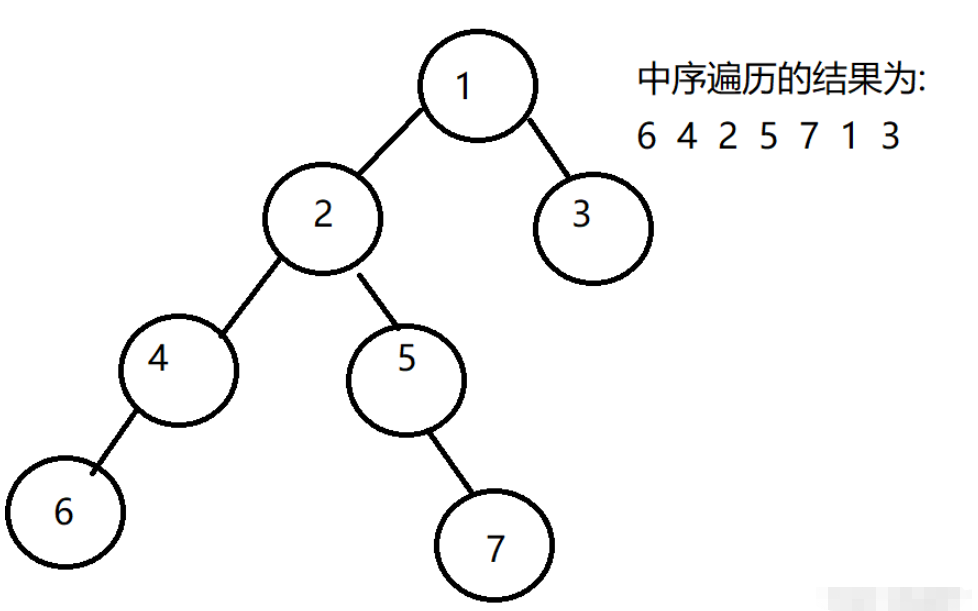
線索化的二叉樹為下, 畫在左邊表示left結點指向,畫在右邊表示right指向,例如7的前驅結點為5,那么7的left指向5,7的后繼節點為1,那么7的right指向1
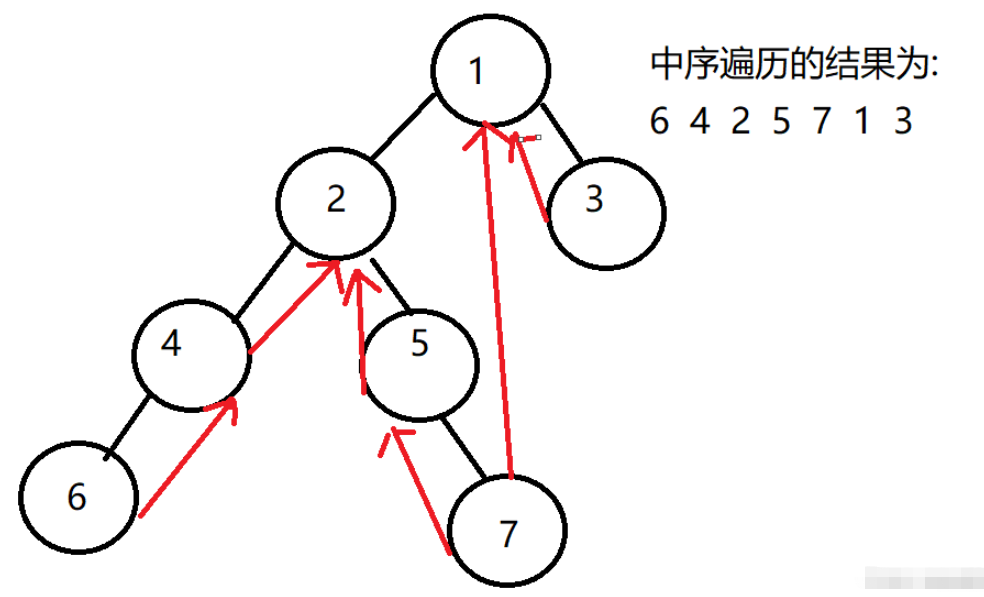
由此,我們可能總結出這樣的結論:中序遍歷二叉樹的指向當前結點的結點為當前結點的左子樹的最右端結點,例如指向1的結點為1的左節點2的最右端結點為7,指向2結點的為2的左節點4的最右端結點4.這一點在之后的morris遍歷中很重要
具體的代碼實現如下:
public class InorderThreadedBinaryTree {
private ThreadTreeNode pre = null;
public void threadedNodes(ThreadTreeNode node) {
//如果node==null,不能線索化
if (node == null) {
return;
}
//1、先線索化左子樹
threadedNodes(node.left);
//2、線索化當前結點
//處理當前結點的前驅結點
//以8為例來理解
//8結點的.left = null,8結點的.leftType = 1
if (node.left == null) {
//讓當前結點的左指針指向前驅結點
node.left = pre;
//修改當前結點的左指針的類型,指向前驅結點
node.leftType = 1;
}
//處理后繼結點
if (pre != null && pre.right == null) {
//讓當前結點的右指針指向當前結點
pre.right = node;
//修改當前結點的右指針的類型=
pre.rightType = 1;
}
//每處理一個結點后,讓當前結點是下一個結點的前驅結點
pre = node;
//3、線索化右子樹
threadedNodes(node.right);
}
}
class ThreadTreeNode {
int val;
ThreadTreeNode left;
//0為非線索化,1為線索化
int leftType;
ThreadTreeNode right;
//0為非線索化,1為線索化
int rightType;
public ThreadTreeNode(int val) {
this.val = val;
}
}但是在實現Morris遍歷的時候,并不需要把結點的左節點線索化,只需要把結點的右節點進行線索化即可,具體的原因在下面進行分析.
上面我們說了Morris遍歷的時候只需要線索化右節點,這里給大家進行解釋.當我們在中序遍歷一棵樹的時候,還比如是這樣一棵樹,我們一步步的node.left來到了6這個結點,這個結點的left為空,所以我們打印6這個結點的值,此時我們需要返回上一個結點,如果我們是要中序遞歸進行遍歷的話,需要返回上一個棧,而我們Morris遍歷的時候無法進行遞歸的返回,所以這個時候我們只需要把6的right結點進行線索化,這個時候6的right指向4,我們就可以返回到4,把4這個結點進行打印,4也線索化返回了2,把2進行打印,然后進行2的right結點5,5的left結點為空,因此打印5,之后進入到5的right結點7,打印7,7的right結點也進行了線索化,進入7的right結點為1,然后打印1,進入3結點并且打印
因為最好不要改變樹的結構,所以我們在打印的時候,將線索化的結點的right結點置為空.
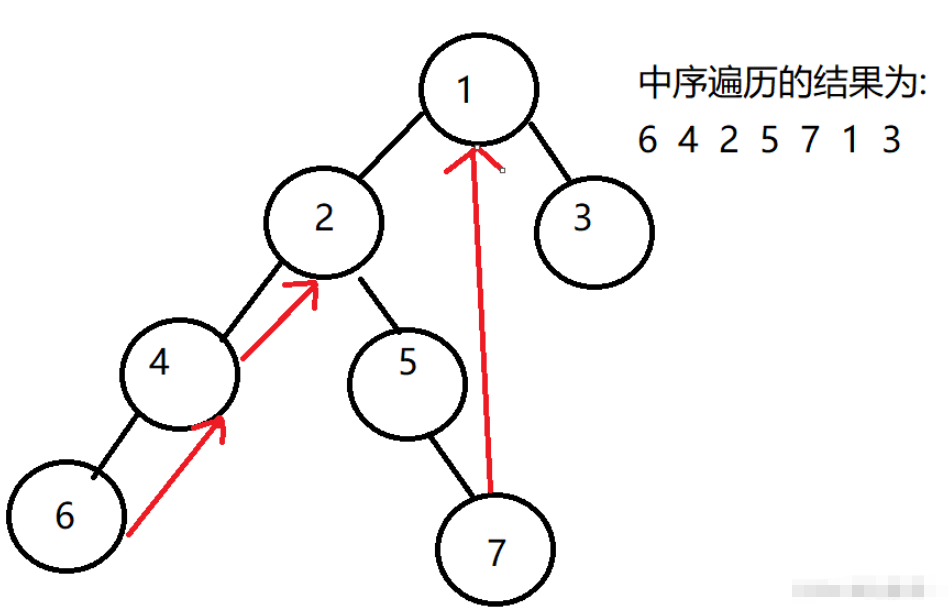
Morris遍歷是利用了線索二叉樹的思想,在遍歷的過程中不適用棧,從而達到了空間復雜度為O(1)
具體的實現如下:
1.初始化當前的結點為根結點
2.若當前的結點的左節點為空,則輸出當前結點,然后遍歷當前結點的右子樹,即'curr=curr.right'
3.若當前結點的左節點不為空,則找到當前結點的前驅節點,即當前結點左節點的最右側結點,記為'prev'
如果'prev.right''為空,則將pre.right指向curr結點,然后遍歷當前結點的左子樹,即'curr=curr.left'
如果'prev.right''不為空,說明已經遍歷完了當前節點的左子樹,斷開 `prev.right` 的連接,即'prev.left=null',輸出當前節點,然后遍歷當前節點的右子樹,即 `curr=curr.right`.
public class Morris {
/**
* 將當前根結點中序遍歷的結果存儲到list集合中
* @param root 根結點
* @return 中序遍歷的結合
*/
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
TreeNode curr = root;
while (curr != null) {
if (curr.left == null) { // 左子樹為空,則輸出當前節點,然后遍歷右子樹
res.add(curr.val); //如果要求直接打印,直接輸出System.out.println(curr.val);
curr = curr.right;
} else {
// 找到當前節點的前驅節點
TreeNode prev = curr.left;
while (prev.right != null && prev.right != curr) {
prev = prev.right;
}
if (prev.right == null) {
// 將前驅節點的右子樹連接到當前節點
prev.right = curr;
curr = curr.left;
} else {
// 前驅節點的右子樹已經連接到當前節點,斷開連接,輸出當前節點,然后遍歷右子樹
prev.right = null;
res.add(curr.val);//如果要求直接打印,直接輸出System.out.println(curr.val);
curr = curr.right;
}
}
}
return res;
}
}
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}測試:
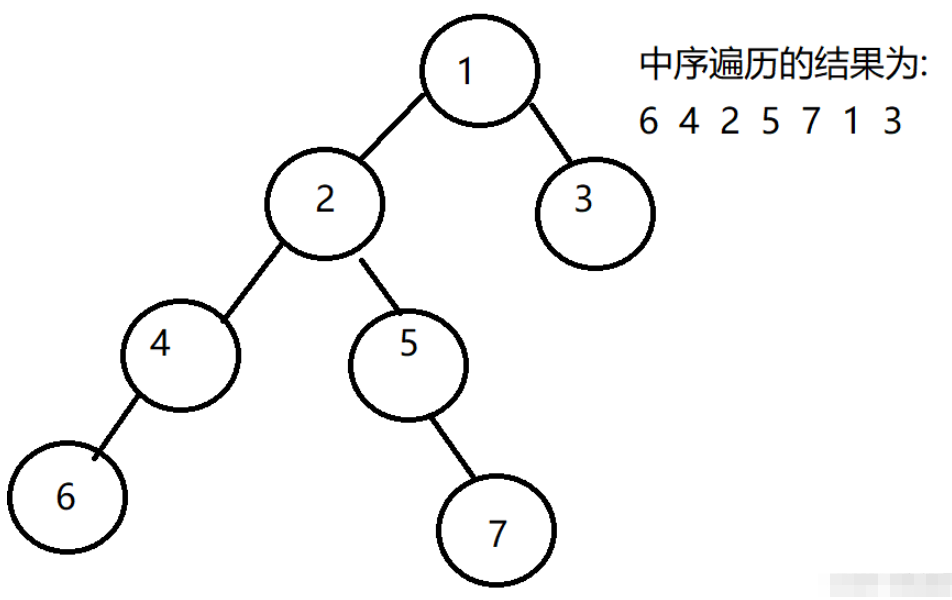
還是這樣一顆二叉樹,輸出如下:
[6, 4, 2, 5, 7, 1, 3]
前序和中序的遍歷很想,只不過在打印(收集結點信息的時候不同),中序遍歷是在當前結點的左節點為空(curr.left==null),或者當前結點已經被線索化(prev.right==curr)的時候進行打印,仔細觀察前序遍歷的過程,我們通過修改打印的順序即可.前序遍歷是在當前結點的左節點為空(curr.left==null),或者當前結點沒有被線索化(prev.right==null)的時候進行打印
具體的思路如下:
1.初始化當前的結點為根結點
2.若當前的結點的左節點為空,則輸出當前結點,然后遍歷當前結點的右子樹,即'curr=curr.right'
3.若當前結點的左節點不為空,則找到當前結點的前驅節點,即當前結點左節點的最右側結點,記為'prev'
如果'prev.right''為空,輸出當前節點,然后將pre.right指向curr結點,然后遍歷當前結點的左子樹,即'curr=curr.left'
如果'prev.right''不為空,說明已經遍歷完了當前節點的左子樹,斷開 `prev.right` 的連接,即'prev.left=null',然后遍歷當前節點的右子樹,即 `curr=curr.right`.
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
TreeNode curr = root;
while (curr != null) {
if (curr.left == null) { // 左子樹為空,則輸出當前節點,然后遍歷右子樹
res.add(curr.val);//如果要求直接打印,直接輸出System.out.println(curr.val);
curr = curr.right;
} else {
// 找到當前節點的前驅節點
TreeNode prev = curr.left;
while (prev.right != null && prev.right != curr) {
prev = prev.right;
}
if (prev.right == null) {
res.add(curr.val);//如果要求直接打印,直接輸出System.out.println(curr.val);
// 將前驅節點的右子樹連接到當前節點
prev.right = curr;
curr = curr.left;
} else {
// 前驅節點的右子樹已經連接到當前節點,斷開連接,輸出當前節點,然后遍歷右子樹
prev.right = null;
curr = curr.right;
}
}
}
return res;
}測試:
public static void main(String[] args) {
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.left.right = new TreeNode(5);
root.left.right.right = new TreeNode(7);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.left.left = new TreeNode(6);
System.out.println(preorderTraversal(root));
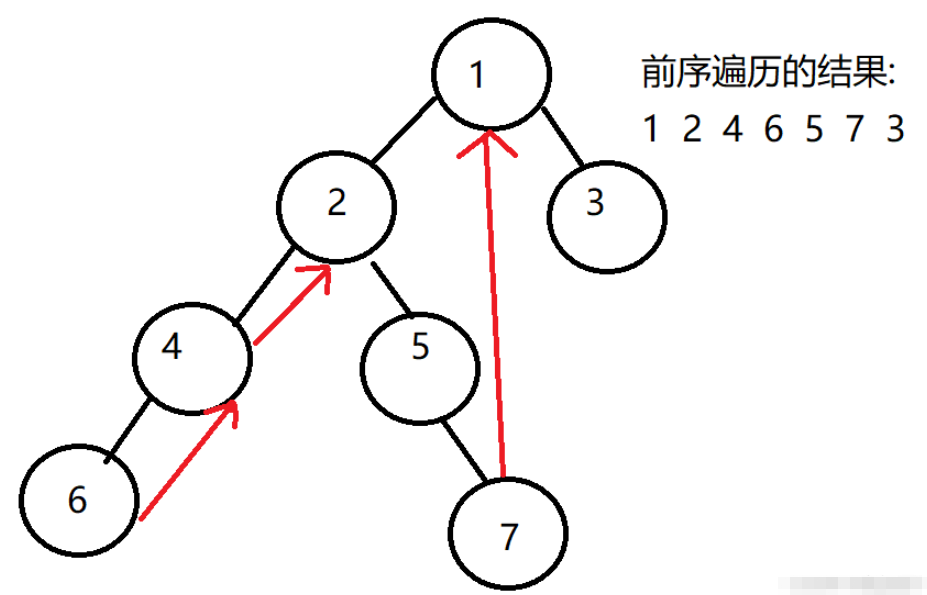
}還是這樣一顆二叉樹,輸出如下:
[1, 2, 4, 6, 5, 7, 3]
后序Morris遍歷實現起來有一定的難度,但是基本代碼還是不變,只是在打印的地方有略微的區別,
具體的思路如下:
1.初始化當前的結點為根結點
2.若當前的結點的左節點為空,則輸出當前結點,然后遍歷當前結點的右子樹,即'curr=curr.right'
3.若當前結點的左節點不為空,則找到當前結點的前驅節點,即當前結點左節點的最右側結點,記為'prev'
如果'prev.right''為空,然后將pre.right指向curr結點,然后遍歷當前結點的左子樹,即'curr=curr.left'
如果'prev.right''不為空,此時進行逆序存儲,說明已經遍歷完了當前節點的左子樹,斷開 `prev.right` 的連接,即'prev.left=null',然后遍歷當前節點的右子樹,即 `curr=curr.right`.
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
TreeNode dump = new TreeNode(0);//建立一個臨時結點
dump.left = root; //設置dump的左節點為root
TreeNode curr = dump; //當前節點為dump
while (curr != null) {
if (curr.left == null) { // 左子樹為空,則輸出當前節點,然后遍歷右子樹
curr = curr.right;
} else {
// 找到當前節點的前驅節點
TreeNode prev = curr.left;
while (prev.right != null && prev.right != curr) {
prev = prev.right;
}
if (prev.right == null) {
// 將前驅節點的右子樹連接到當前節點
prev.right = curr;
curr = curr.left;
} else {
reverseAddNodes(curr.left, prev, res);
// 前驅節點的右子樹已經連接到當前節點,斷開連接,輸出當前節點,然后遍歷右子樹
prev.right = null;
curr = curr.right;
}
}
}
return res;
}
private void reverseAddNodes(TreeNode begin, TreeNode end, List<Integer> res) {
reverseNodes(begin, end); //將begin到end的進行逆序連接
TreeNode curr = end;
while (true) {//將逆序連接后端begin到end添加
res.add(curr.val);
if (curr == begin)
break;
curr = curr.right;
}
reverseNodes(end, begin);//恢復之前的連接狀態
}
/**
* 將begin到end的進行逆序連接
*
* @param begin
* @param end
*/
private void reverseNodes(TreeNode begin, TreeNode end) {
TreeNode prev = begin;
TreeNode curr = prev.right;
TreeNode post;
while (prev != end) {
post = curr.right;
curr.right = prev;
prev = curr;
curr = post;
}
}測試:
public static void main(String[] args) {
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.left.right = new TreeNode(5);
root.left.right.right = new TreeNode(7);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.left.left = new TreeNode(6);
System.out.println(postorderTraversal(root));
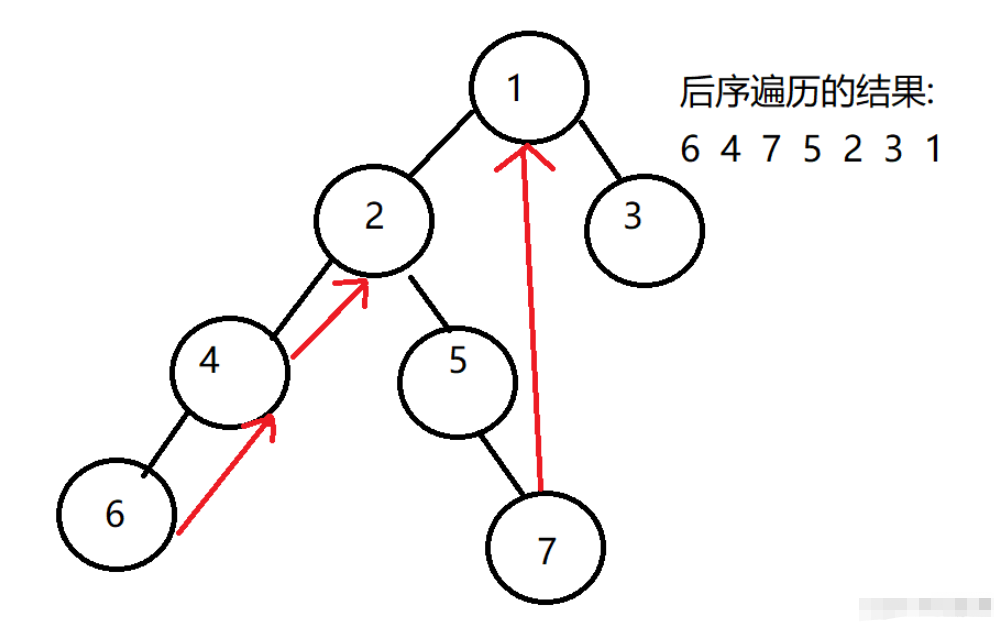
}還是這樣一顆二叉樹,輸出如下:
[6, 4, 7, 5, 2, 3, 1]
關于“Java Morris遍歷算法及在二叉樹中應用的方法是什么”這篇文章的內容就介紹到這里,感謝各位的閱讀!相信大家對“Java Morris遍歷算法及在二叉樹中應用的方法是什么”知識都有一定的了解,大家如果還想學習更多知識,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。