溫馨提示×
您好,登錄后才能下訂單哦!
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好,登錄后才能下訂單哦!
這篇“Python怎么通過手肘法實現k_means聚類”文章的知識點大部分人都不太理解,所以小編給大家總結了以下內容,內容詳細,步驟清晰,具有一定的借鑒價值,希望大家閱讀完這篇文章能有所收獲,下面我們一起來看看這篇“Python怎么通過手肘法實現k_means聚類”文章吧。
import matplotlib.pylab as plt import numpy as np
# 計算兩點距離 def distance(a, b): return np.sqrt((a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2)
# 取集合中心點 def means(arr): x = 0 y = 0 for i in range(len(arr)): x += arr[i][0] y += arr[i][1] if len(arr) > 0: x /= len(arr) y /= len(arr) return np.array([x, y])
# 尋找距離已加入聚類中心數組最遠的點,用于初始化聚類中心 def farthest(k_arr, arr): point = [0, 0] max_dist = 0 for e in arr: dist = 0 for i in range(len(k_arr)): dist += distance(k_arr[i], e) if dist > max_dist: max_dist = dist point = e return point
(1)先讀取表中的數據
(2)如何隨機獲取其中一個點作為第一個聚類中心
(3)接下來每次獲取距離之間所有聚類中心點最遠的點作為下一個聚類中心點
(4)每次迭代時,遍歷集合中的所有點,將其加入距離最小的聚類中心點數組中,更新聚類中心
(5)最后將數據可視化,返回分類好的數組
def k_means(k):
# 讀取數據
kmeans_data = np.genfromtxt('kmeans_data.txt', dtype=float)
# 初始化
r = np.random.randint(len(kmeans_data) - 1)
k_arr = np.array([kmeans_data[r]])
class_arr = [[]]
for i in range(k - 1):
k_arr = np.concatenate([k_arr, np.array([farthest(k_arr, kmeans_data)])])
class_arr.append([])
# 迭代聚類
n = 20
class_temp = class_arr
for i in range(n): # 迭代次數
class_temp = class_arr
for e in kmeans_data: # 把集合中的每一個點聚到離它最近的類
k_idx = 0 # 假設距離第一個聚類中心最近
min_d = distance(e, k_arr[0])
for j in range(len(k_arr)): # 獲取距離該元素最近的聚類中心
if distance(e, k_arr[j]) < min_d:
min_d = distance(e, k_arr[j])
k_idx = j
class_temp[k_idx].append(e) # 把該元素加到對應的類中
# 更新聚類中心
for l in range(len(k_arr)):
k_arr[l] = means(class_temp[l])
# 將數據可視化
col = ['red', 'blue', 'yellow', 'green', 'pink', 'black', 'purple', 'orange', 'brown']
for i in range(k):
plt.scatter(k_arr[i][0], k_arr[i][1], linewidths=10, color=col[i])
plt.scatter([e[0] for e in class_temp[i]], [e[1] for e in class_temp[i]], color=col[i])
plt.show()
# 返回分類好的簇
return class_temp(1)遍歷k值的范圍,從1到9
(2)kmeans獲取分類好的數組
(3)遍歷kmeans計算對應的SSE
(4)畫出對應k值的SSE的折線圖
# 通過肘部觀察法獲取k值
def getK():
mean_dist = []
for k in range(1, 10):
# 獲取分成k簇后的元素
kmeans = k_means(k)
sse = 0
# 計算SSE
for i in range(len(kmeans)):
mean = means(kmeans[i])
for e in kmeans[i]:
sse += distance(mean, e) ** 2
mean_dist.append(sse)
# 化成折線圖觀察最佳的k值
plt.plot(range(1, 10), mean_dist, 'bx-')
plt.ylabel('SSE')
plt.xlabel('k')
plt.show()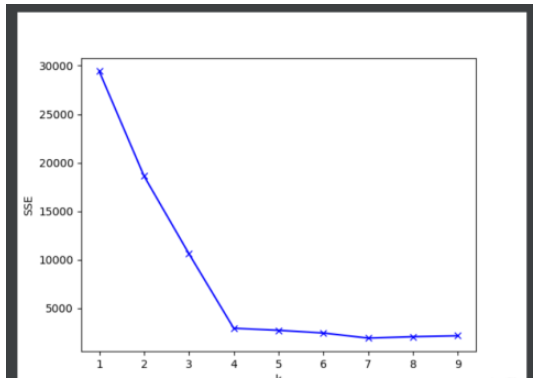
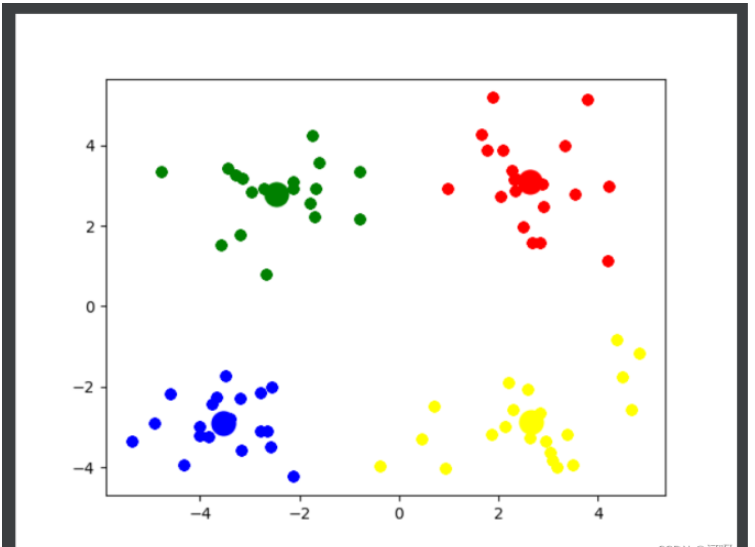
if __name__ == '__main__': getK() # 通過觀察可知, 4 是最佳的k值 k_means(4)
import matplotlib.pylab as plt
import numpy as np
# 計算兩點距離
def distance(a, b):
return np.sqrt((a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2)
# 取集合中心點
def means(arr):
x = 0
y = 0
for i in range(len(arr)):
x += arr[i][0]
y += arr[i][1]
if len(arr) > 0:
x /= len(arr)
y /= len(arr)
return np.array([x, y])
# 尋找距離已加入聚類中心數組最遠的點,用于初始化聚類中心
def farthest(k_arr, arr):
point = [0, 0]
max_dist = 0
for e in arr:
dist = 0
for i in range(len(k_arr)):
dist += distance(k_arr[i], e)
if dist > max_dist:
max_dist = dist
point = e
return point
def k_means(k):
# 讀取數據
kmeans_data = np.genfromtxt('kmeans_data.txt', dtype=float)
# 初始化
r = np.random.randint(len(kmeans_data) - 1)
k_arr = np.array([kmeans_data[r]])
class_arr = [[]]
for i in range(k - 1):
k_arr = np.concatenate([k_arr, np.array([farthest(k_arr, kmeans_data)])])
class_arr.append([])
# 迭代聚類
n = 20
class_temp = class_arr
for i in range(n): # 迭代次數
class_temp = class_arr
for e in kmeans_data: # 把集合中的每一個點聚到離它最近的類
k_idx = 0 # 假設距離第一個聚類中心最近
min_d = distance(e, k_arr[0])
for j in range(len(k_arr)): # 獲取距離該元素最近的聚類中心
if distance(e, k_arr[j]) < min_d:
min_d = distance(e, k_arr[j])
k_idx = j
class_temp[k_idx].append(e) # 把該元素加到對應的類中
# 更新聚類中心
for l in range(len(k_arr)):
k_arr[l] = means(class_temp[l])
# 將數據可視化
col = ['red', 'blue', 'yellow', 'green', 'pink', 'black', 'purple', 'orange', 'brown']
for i in range(k):
plt.scatter(k_arr[i][0], k_arr[i][1], linewidths=10, color=col[i])
plt.scatter([e[0] for e in class_temp[i]], [e[1] for e in class_temp[i]], color=col[i])
plt.show()
# 返回分類好的簇
return class_temp
# 通過肘部觀察法獲取k值
def getK():
mean_dist = []
for k in range(1, 10):
# 獲取分成k簇后的元素
kmeans = k_means(k)
sse = 0
# 計算SSE
for i in range(len(kmeans)):
mean = means(kmeans[i])
for e in kmeans[i]:
sse += distance(mean, e) ** 2
mean_dist.append(sse)
# 化成折線圖觀察最佳的k值
plt.plot(range(1, 10), mean_dist, 'bx-')
plt.ylabel('SSE')
plt.xlabel('k')
plt.show()
if __name__ == '__main__':
getK()
# 通過觀察可知, 4 是最佳的k值
k_means(4)以上就是關于“Python怎么通過手肘法實現k_means聚類”這篇文章的內容,相信大家都有了一定的了解,希望小編分享的內容對大家有幫助,若想了解更多相關的知識內容,請關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。