您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本文小編為大家詳細介紹“基于Python如何實現模擬三體運動”,內容詳細,步驟清晰,細節處理妥當,希望這篇“基于Python如何實現模擬三體運動”文章能幫助大家解決疑惑,下面跟著小編的思路慢慢深入,一起來學習新知識吧。
此前所做的一切三體和太陽系的動畫,都是基于牛頓力學的,而且直接對微分進行差分化,從而精度非常感人,用不了幾年就得撞一起去。
為了給三體人提供一個更加有價值的推導,這次通過求解拉格朗日方程的數值解來實現。
首先假設三個質點的質量分別為m1, m2,m3,坐標為x→1,x→2,x→3,質點速度可以表示為x → ˙.假設三體在二維平面上運動,則第i個質點的動能為
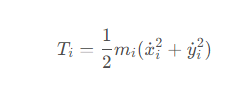
引力勢能為
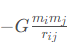
其中G為萬有引力常量,rij為質點i,j之間的距離,則系統的拉格朗日量為
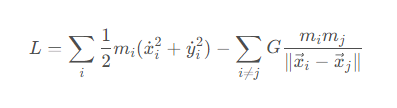
有了拉格朗日量,將其帶入拉格朗日方程
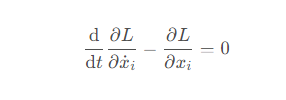
就可以得到拉格朗日方程組。
對于三體系統而言,總計有3個粒子,每個粒子有x,y兩個自由度,也就是說最后會得到6組方程。考慮到公式推導過程中可能會出現錯誤,所以下面采用sympy來進行公式推導。
首先定義符號變量
from sympy import symbols
from sympy.physics.mechanics import dynamicsymbols
m = symbols('m1:4')
x = dynamicsymbols('x1:4')
y = dynamicsymbols('y1:4')接下來,需要構造系統的拉格朗日量L,其實質是系統的動能減去勢能,對于上面構建的三體系統而言,動能和勢能可分別表示為
計算每個質點的動能和勢能。動能是由速度決定的,而速度是由位置對時間的導數決定的。我們可以用 sympy 的 diff 函數來求導:
from sympy import diff # 此為速度的平方 v2 = [diff(x[i],t)**2 + diff(y[i])**2 for i in range(3)] T = 0 for i in range(3): T += m[i]*v2[i]/2
勢能是由萬有引力決定的,而萬有引力是由兩個質點之間的距離決定的。我們可以用 sympy 的 sqrt 函數來求距離:
from sympy import sqrt,cos
G = symbols('G') # 引力常數
ijs = [(0,1), (0,2),(1,2)]
dij = [sqrt((x[i]-x[j])**2+(y[i]-y[j])**2) for i,j in ijs]
U = 0
for k in range(3):
i,j = ijs[k]
U -= G*m[i]*m[j]/dij[k]有了動能和勢能,就可以愉快地求拉格朗日量了,有了拉格朗日量,就可以列拉格朗日方程了
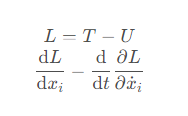
三個粒子的每一個坐標維度,都可以列出一組拉格朗日方程,所以總共有6個拉格朗日方程組
from sympy import solve L = T - U eqLag = lambda x : diff(L, x)-diff(diff(L, diff(x, t)), t) # 拉格朗日方程組 eqs = [eqLag(xi) for xi in x+y]
記xij=xi−xj,yij=yi−yj ,則
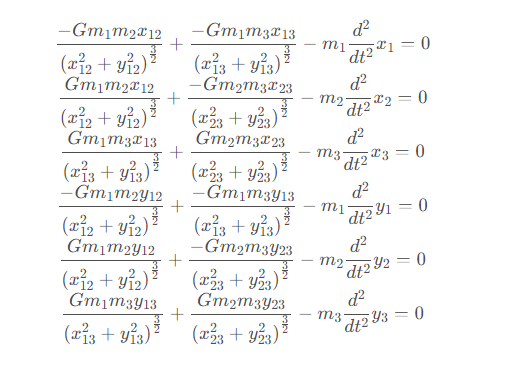
接下來就要調用Python的odeint來計算這個微分方程組的數值解,odeint的調用方法大致為odeint(func, y, t, args),其中func是一個函數,這個函數必須為func(y,t,...),且返回值為dy/dt.
為此,需要將上述方程組再行拆分,以消去其中的二次導數,以x1為例,令u1=dx1/dt ,則此方程變為方程組
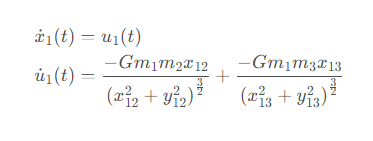
由于三體系統中有3個粒子,共6個獨立變量,所以要列12個方程。記
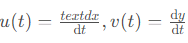
則odeint輸入的y的形式為
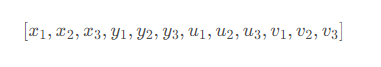
從而func的具體形式為
import numpy as np dxy = lambda x,y : np.sqrt(x**2+y**2)**(3/2) def triSys(Y, t, m, G): jk = [(1,2),(0,2),(0,1)] x,y = Y[:3], Y[3:6] u,v = Y[6:9], Y[9:] du, dv = [], [] for i in range(3): j, k = jk[i] xji, xki = x[j]-x[i], x[k]-x[i] yji, yki = y[j]-y[i], y[k]-y[i] dji, dki = dxy(xji, yji), dxy(yji, yki) mji, mki = G*m[i]*m[j], G*m[i]*m[k] du.append(mji*xji/dji + mki*xki/dki) dv.append(mji*yji/dji + mki*yki/dki) dydt = [*u, *v, *du, *dv] return dydt
接下來就是見證奇跡的時刻,首先創建一個隨機的起點,作為三體運動的初值,然后帶入開整就完事兒了
from scipy.integrate import odeint np.random.seed(42) y0 = np.random.rand(12) m = np.random.rand(3) t = np.linspace(0, 20, 1001) sol = odeint(triSys, y0, t, args=(m, 1))
然后繪制一下這三顆星的軌跡
import matplotlib.pyplot as plt plt.plot(sol[:,0], sol[:,3]) plt.plot(sol[:,1], sol[:,4]) plt.plot(sol[:,2], sol[:,5]) plt.show()
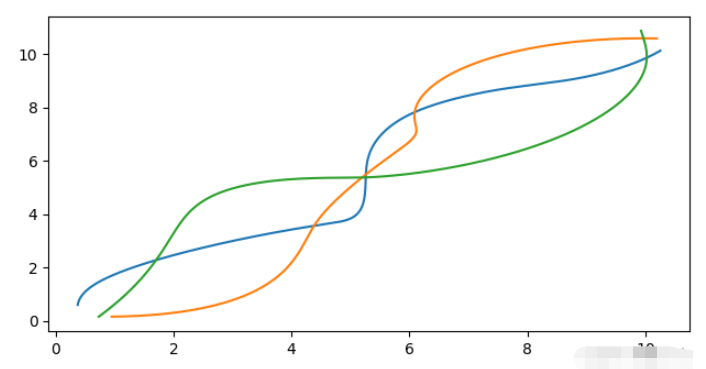
光是看這個軌跡就十分驚險了有木有。
如果把其中的第一顆星作為坐標原點,那么另外兩顆星的軌跡大致為
plt.plot(sol[:,1]-sol[:,0], sol[:,4]-sol[:,3]) plt.plot(sol[:,2]-sol[:,0], sol[:,5]-sol[:,3]) plt.scatter([0],[0], c='g', marker='*') plt.show()
結果為
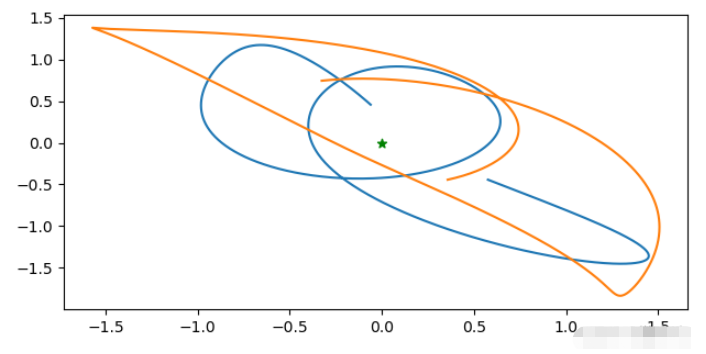
最后,以中間這顆星為原點,繪制一下另外兩顆星運動的動態過程
import matplotlib.animation as animation
fig = plt.figure(figsize=(9,4))
ax = fig.add_subplot(xlim=(-1.8,1.8),ylim=(-1.8,1.5))
ax.grid()
traces = [ax.plot([],[],'-',lw=0.5)[0] for _ in range(2)]
pts = [ax.plot([],[] ,marker='*')[0] for _ in range(2)]
ax.plot([0],[0], marker="*", c='r')
X1 = sol[:,1]-sol[:,0]
Y1 = sol[:,4]-sol[:,3]
X2 = sol[:,2]-sol[:,0]
Y2 = sol[:,5]-sol[:,3]
def animate(n):
traces[0].set_data(X1[:n], Y1[:n])
traces[1].set_data(X2[:n], Y2[:n])
pts[0].set_data([X1[n], Y1[n]])
pts[1].set_data([X2[n], Y2[n]])
return traces + pts
ani = animation.FuncAnimation(fig, animate,
range(1000), interval=10, blit=True)
ani.save('tri.gif')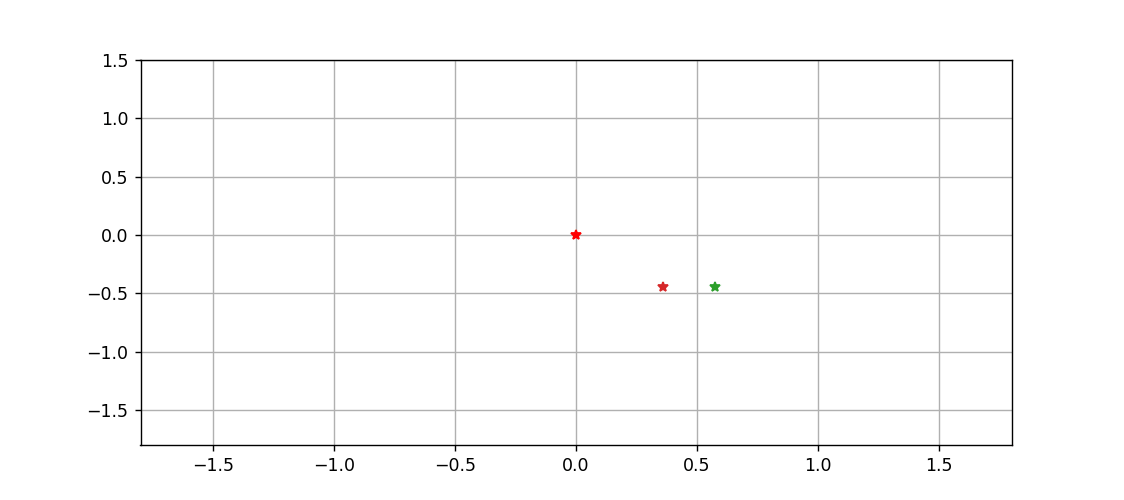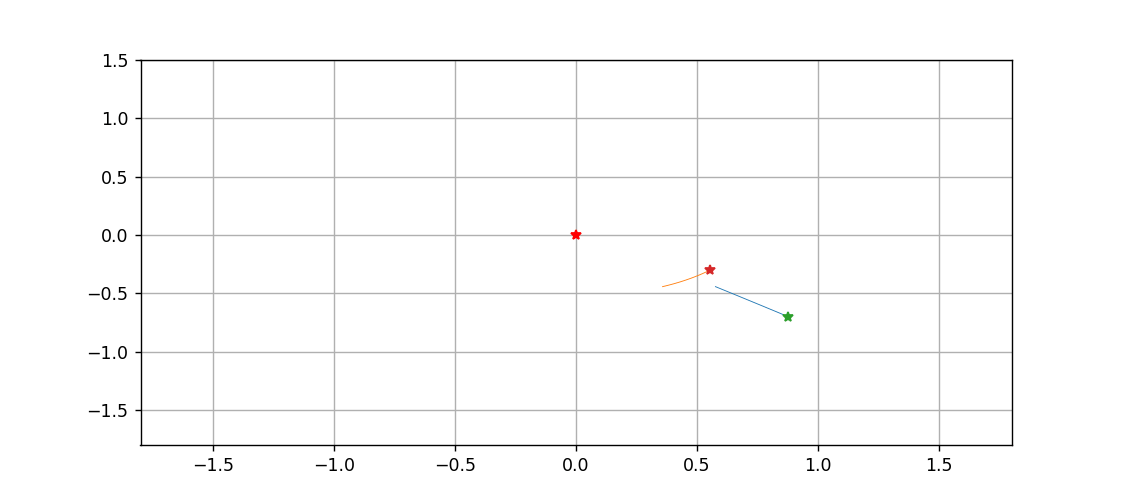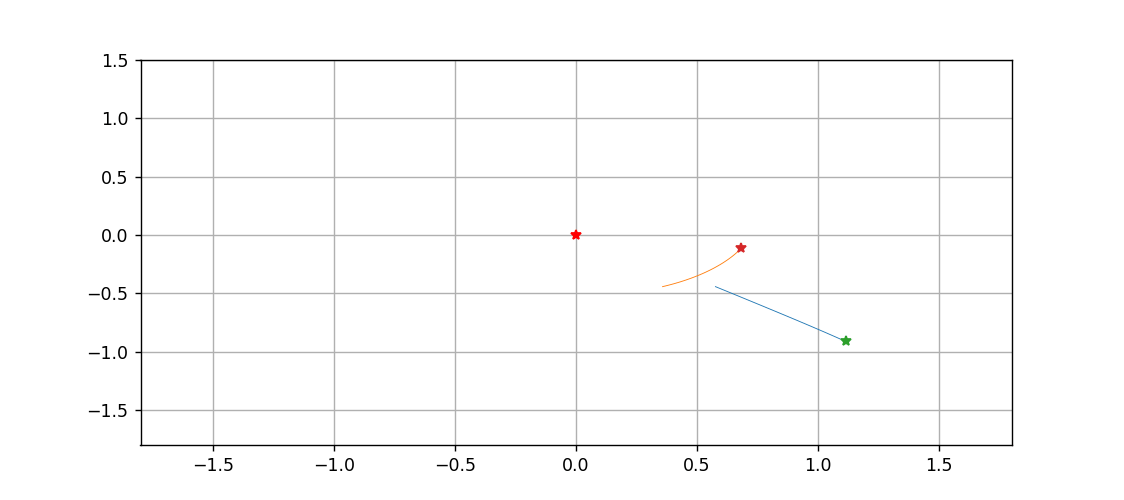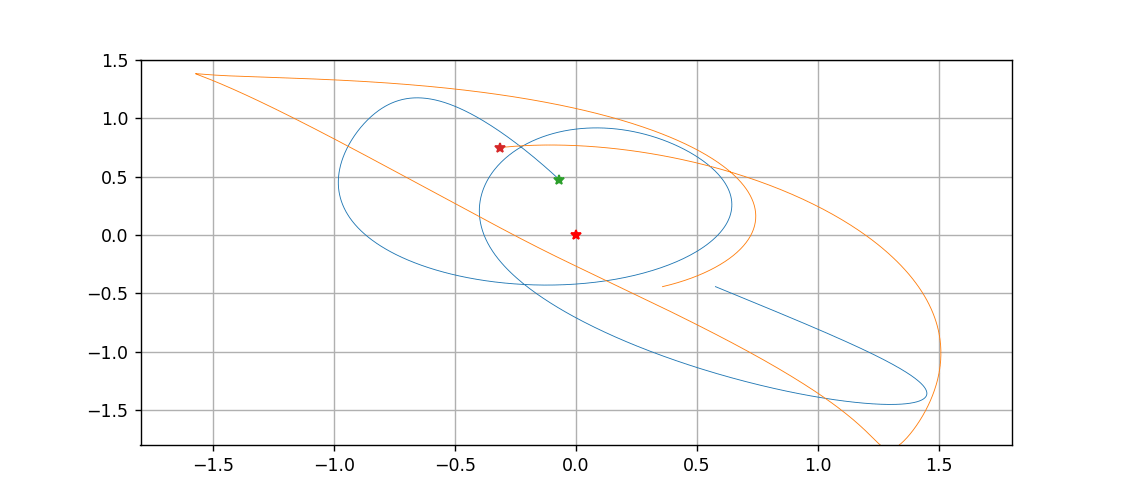
讀到這里,這篇“基于Python如何實現模擬三體運動”文章已經介紹完畢,想要掌握這篇文章的知識點還需要大家自己動手實踐使用過才能領會,如果想了解更多相關內容的文章,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。