您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本文小編為大家詳細介紹“Python基于歐拉角怎么繪制一個立方體”,內容詳細,步驟清晰,細節處理妥當,希望這篇“Python基于歐拉角怎么繪制一個立方體”文章能幫助大家解決疑惑,下面跟著小編的思路慢慢深入,一起來學習新知識吧。
工欲善其事、必先利其器,在開始學習歐拉角模擬之前,可先繪制一個立方體。
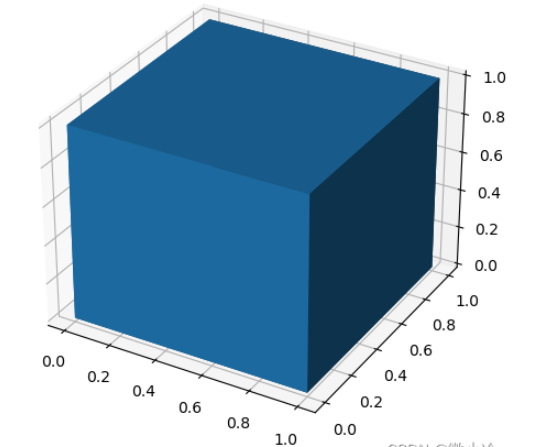
在matplotlib中,這個任務可通過plt.voxels實現,下面先繪制一個最質樸的立方體
代碼為
import matplotlib.pyplot as plt import numpy as np x, y, z = np.indices((2, 2, 2)) filled = np.ones((1,1,1)) ax = plt.subplot(projection='3d') ax.voxels(x,y,z, filled=filled) plt.show()
其中,x,y,z表示頂點,filled表示被填充的區域。由于其頂點數量為2×2×2,故只有一個立方體,從而filled是一個1×1×1的張量。
有了立方體之后,就可以進行歐拉角仿真了。
為了盡快進入演示部分,故對原理的介紹從略,僅從二維平面上的旋轉矩陣出發,做一個簡單的推導,而三維旋轉矩陣,至少在形式上與二維是雷同的。
假設坐標系中有一個向量(x,y),其模長為r=√x2+y2,角度為θ0=arctan(y/x).若將其圍繞坐標原點逆時針旋轉θ,則其坐標變為
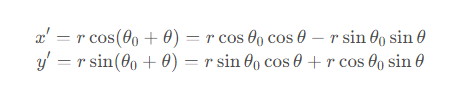
由于x=rcosθ0, y=rsinθ0,則上式可以寫為
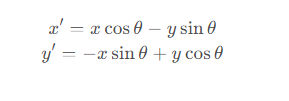
寫成矩陣形式即為
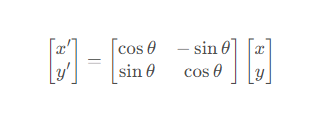
也就是說,在平面直角坐標系上,向量繞原點順時針旋轉θ,相當于左乘一個旋轉矩陣。
推廣到三維,為了限制xy坐標平面上的旋轉,要將其旋轉中心從原點擴展為繞著z軸旋轉,從而三維旋轉矩陣可推廣為
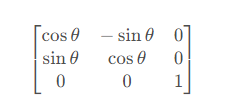
同理可得到繞三個軸轉動的旋轉矩陣,為了書寫方便,記Sθ=sinθ,Cθ=cosθ,可列出下表。

將旋轉矩陣寫成函數是十分方便的,下面用lambda表達式來實現
import numpy as np # 將角度轉弧度后再求余弦 cos = lambda th : np.cos(np.deg2rad(th)) sin = lambda th : np.sin(np.deg2rad(th)) # 即 Rx(th) => Matrix Rx = lambda th : np.array([ [1, 0, 0], [0, cos(th), -sin(th)], [0, sin(th), cos(th)]]) Ry = lambda th : np.array([ [cos(th), 0, sin(th)], [0 , 1, 0], [-sin(th), 0, cos(th)] ]) Rz = lambda th : np.array([ [cos(th) , sin(th), 0], [-sin(th), cos(th), 0], [0 , 0, 1]])
有了旋轉矩陣,就可以旋轉,接下來讓正方體沿著三個軸分別旋轉30°,其效果如下
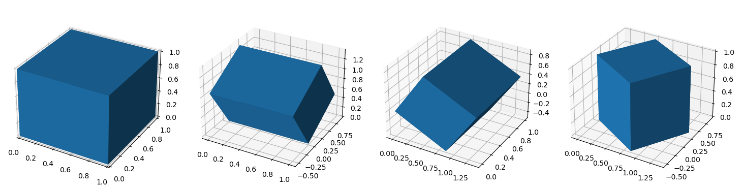
由于ax.voxels在繪圖時,要求輸入的是擁有三個維度的數組,而旋轉矩陣是3 × 3 3\times33×3矩陣,相當于是二維數組,彼此之間可能很難計算,所以實際計算時,需要對數組維度進行調整
import matplotlib.pyplot as plt
# 用于批量調節x,y,z的數組維度
Reshape = lambda x,y,z : [x.reshape(2,2,2), y.reshape(2,2,2), z.reshape(2,2,2)]
filled = np.ones((1,1,1))
x, y, z = np.indices((2, 2, 2))
# 將x,y,z展開,以便于矩陣計算
xyz = np.array([x,y,z]).reshape(3,-1)
fig = plt.figure("rotate")
# 此為未旋轉的正方體
ax = fig.add_subplot(1,4,1, projection='3d')
ax.voxels(x,y,z, filled=filled)
# 繞x軸旋轉30°
X, Y, Z = Rx(30) @ xyz
ax = fig.add_subplot(1,4,2, projection='3d')
ax.voxels(*Reshape(X, Y, Z), filled=filled)
# 繞y軸旋轉30°
X, Y, Z = Ry(30) @ xyz
ax = fig.add_subplot(1,4,3, projection='3d')
ax.voxels(*Reshape(X, Y, Z), filled=filled)
# 繞z軸旋轉30°
X, Y, Z = Rz(30) @ xyz
ax = fig.add_subplot(1,4,4, projection='3d')
ax.voxels(*Reshape(X, Y, Z), filled=filled)
plt.show()眾所周知,矩陣計算是不能交換的,反映到實際生活中,就是不同的旋轉次序,可能會導致完全不同的結果,接下來沿著不同的旋轉次序,來對正方體進行旋轉,效果如下
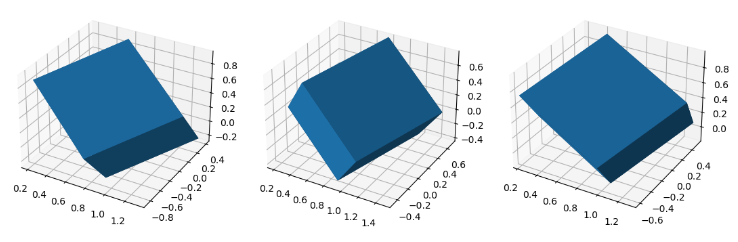
需要注意的是,由于矩陣左乘向量表示對向量進行旋轉,所以距離向量最近的矩陣表示最先進行的操作,即RzRyRxr ? 表示先轉Rx ,Ry次之,Rz最后。
代碼如下
filled = np.ones((1,1,1))
x, y, z = np.indices((2, 2, 2))
xyz = np.array([x,y,z]).reshape(3,-1)
fig = plt.figure("rotate")
# 旋轉順序 x, y, z
X, Y, Z = Rz(30) @ Ry(30) @ Rx(30) @ xyz
ax = fig.add_subplot(1,3,1, projection='3d')
ax.voxels(*Reshape(X, Y, Z), filled=filled)
# 旋轉順序 z, y, x
X, Y, Z = Rx(30) @ Ry(30) @ Rz(30) @ xyz
ax = fig.add_subplot(1,3,2, projection='3d')
ax.voxels(*Reshape(X, Y, Z), filled=filled)
# 旋轉順序 y, x, z
X, Y, Z = Rz(30) @ Rx(30) @ Ry(30) @ xyz
ax = fig.add_subplot(1,3,3, projection='3d')
ax.voxels(*Reshape(X, Y, Z), filled=filled)
plt.show()總之,雖然分不清誰是誰,但最起碼可以看清楚,不同的旋轉順序的確導致了不同的旋轉結果。
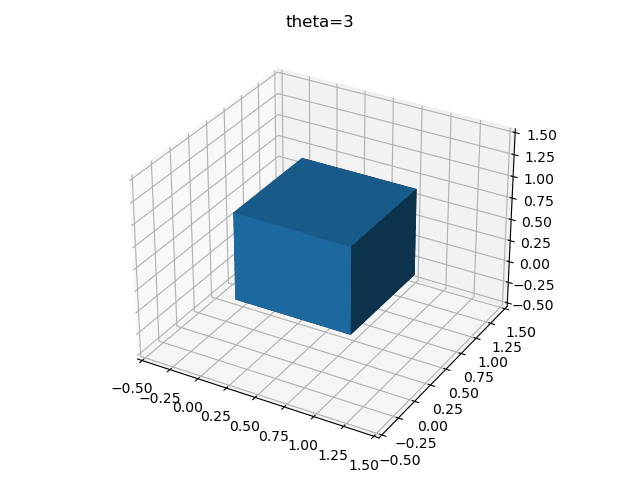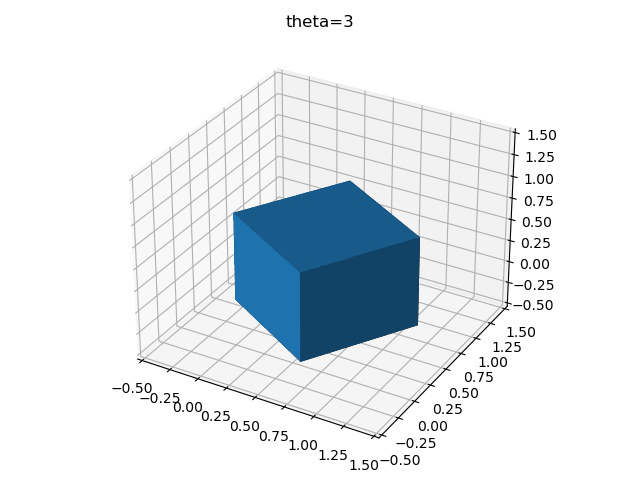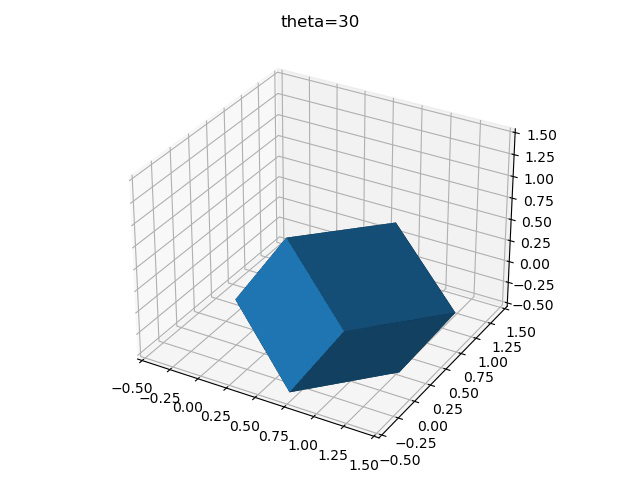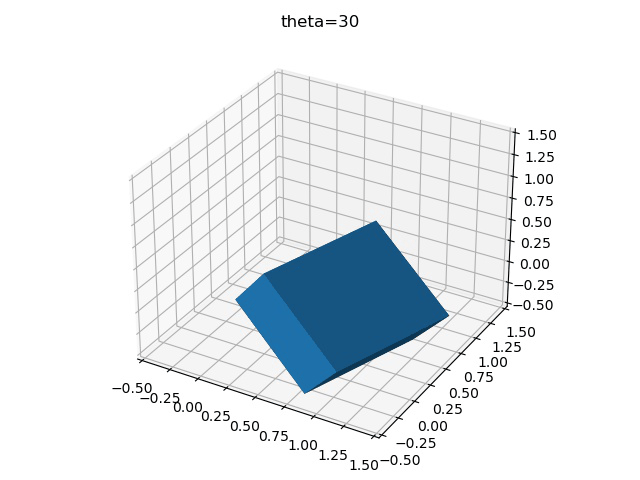
為了更加清楚地表示這一過程,可以將正方體的旋轉過程繪制下來,先考慮單軸旋轉,假設每次旋轉3°,繞X軸旋轉30次,則可得到
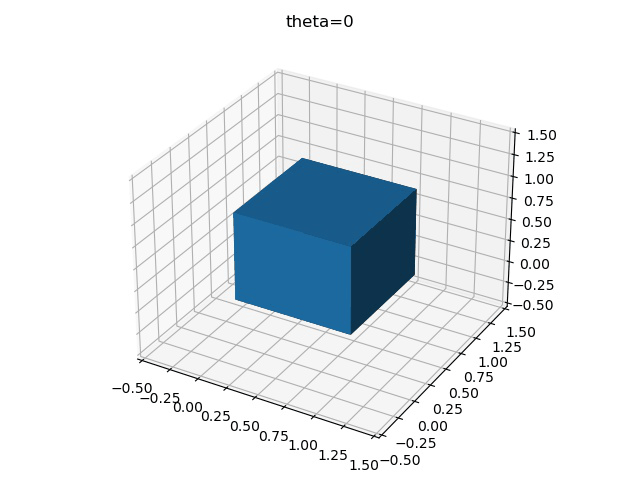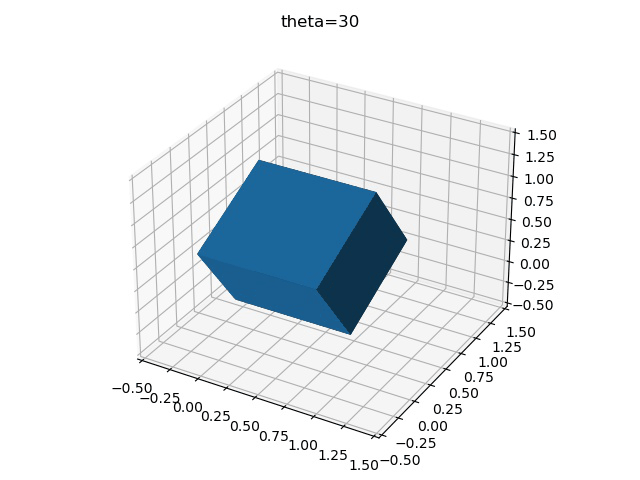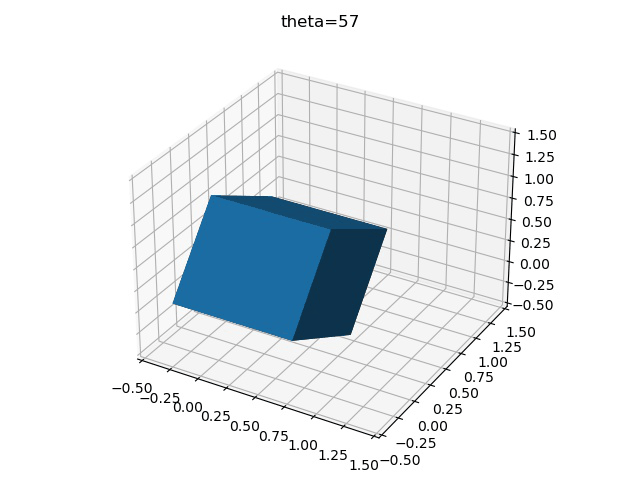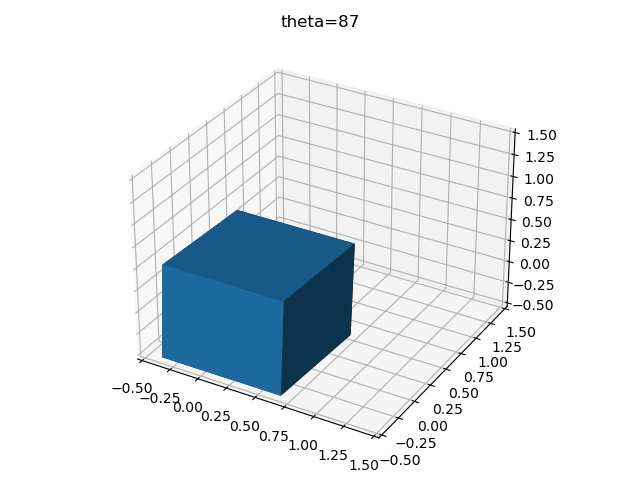
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
import imageio
filled = np.ones((1,1,1))
x, y, z = np.indices((2, 2, 2))
xyz = np.array([x,y,z]).reshape(3,-1)
def saveGif(X,Y,Z, gifs):
plt.cla()
ax = plt.subplot(projection='3d')
ax.voxels(*Reshape(X, Y, Z), filled=filled)
ax.set_xlim(-0.5,1.5)
ax.set_ylim(-0.5,1.5)
ax.set_zlim(-0.5,1.5)
ax.set_title(f"theta={th}")
plt.tight_layout()
plt.savefig(f"tmp.jpg")
gifs.append(imageio.imread(f"tmp.jpg"))
gifImgs = []
th = 0
for i in range(30):
X,Y,Z = Rx(th)@xyz
th += 3
saveGif(X, Y, Z, gifImgs)
imageio.mimsave("test.gif",gifImgs,fps=10)通過這個方法,可以將不同順序的旋轉矩陣可視化表示,
filled = np.ones((1,1,1))
x, y, z = np.indices((2, 2, 2))
xyz = np.array([x,y,z]).reshape(3,-1)
gifImgs = []
th = 0
for _ in range(10):
X,Y,Z = Rz(0) @ Rx(0) @ Ry(th) @ xyz
th += 3
saveGif(X, Y, Z, gifImgs)
th = 0
for i in range(10):
X,Y,Z = Rz(0) @ Rx(th) @ Ry(30) @ xyz
th += 3
saveGif(X, Y, Z, gifImgs)
th = 0
for i in range(10):
X,Y,Z = Rz(th) @ Rx(30) @ Ry(30) @ xyz
th += 3
saveGif(X, Y, Z, gifImgs)
imageio.mimsave("test.gif",gifImgs,fps=10)最后得到三種不同旋轉順序的區別
x-y-z
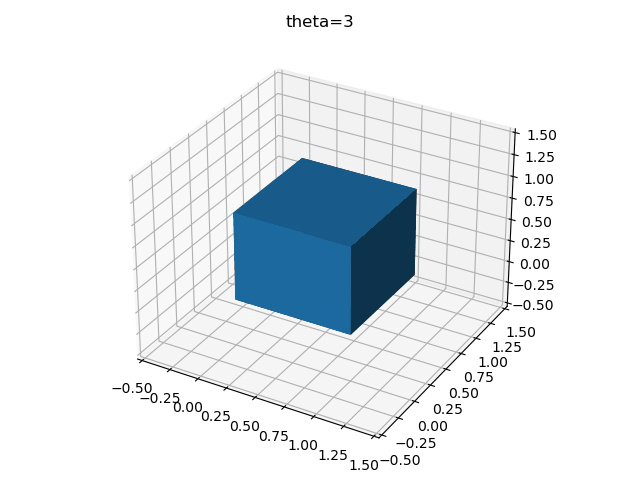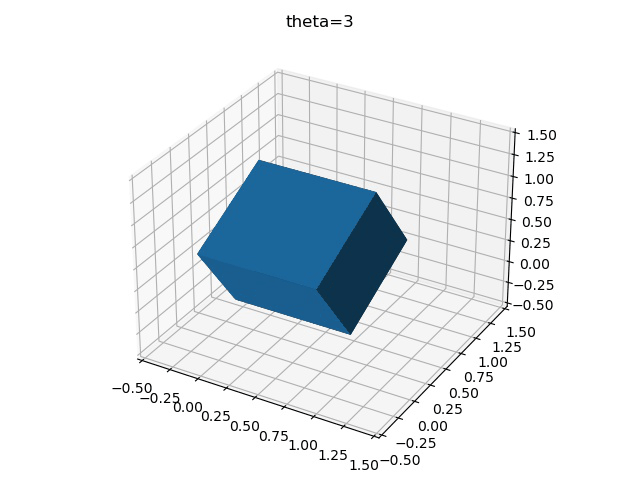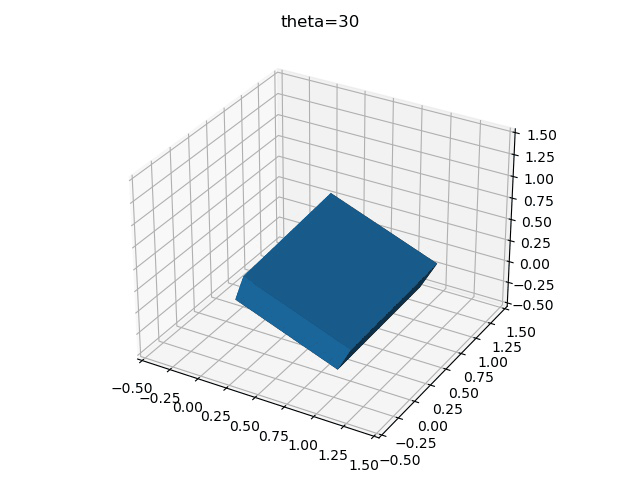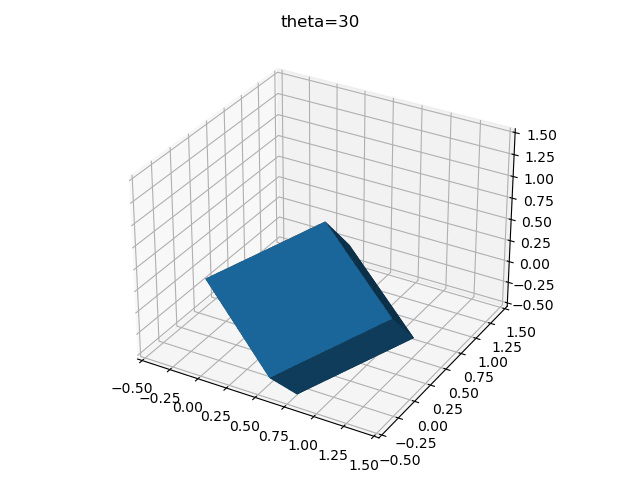
z-y-x
y-x-z
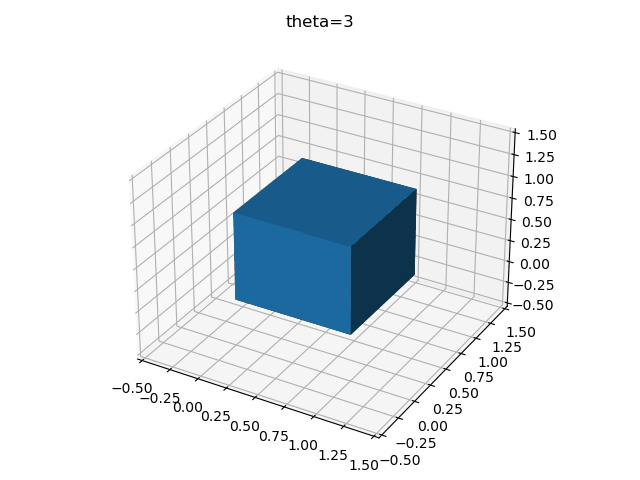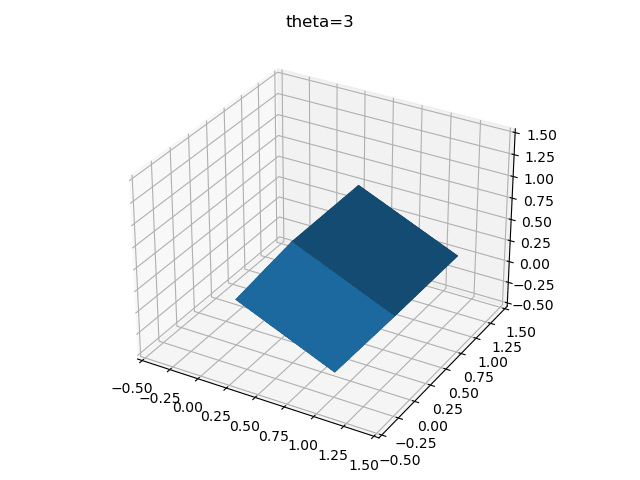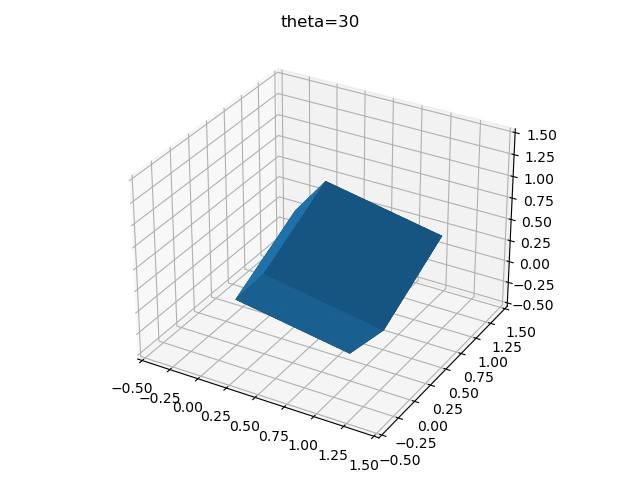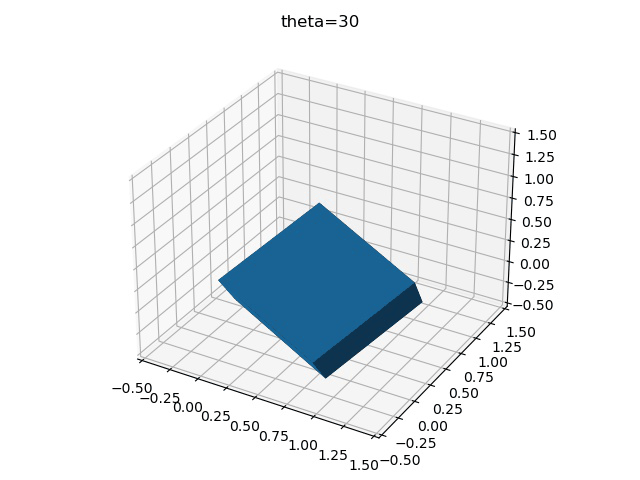
讀到這里,這篇“Python基于歐拉角怎么繪制一個立方體”文章已經介紹完畢,想要掌握這篇文章的知識點還需要大家自己動手實踐使用過才能領會,如果想了解更多相關內容的文章,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。