您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
今天小編給大家分享一下Python如何實現兩種稀疏矩陣的最小二乘法的相關知識點,內容詳細,邏輯清晰,相信大部分人都還太了解這方面的知識,所以分享這篇文章給大家參考一下,希望大家閱讀完這篇文章后有所收獲,下面我們一起來了解一下吧。
scipy.sparse.linalg實現了兩種稀疏矩陣最小二乘法lsqr和lsmr,前者是經典算法,后者來自斯坦福優化實驗室,據稱可以比lsqr更快收斂。
這兩個函數可以求解Ax=b,或arg minx ∥Ax−b∥2,或arg minx ∥Ax−b∥2 +d2∥x−x0∥2,其中A必須是方陣或三角陣,可以有任意秩。
通過設置容忍度at ,bt,可以控制算法精度,記r=b-Ax 為殘差向量,如果Ax=b是相容的,lsqr在∥r∥?at∗∥A∥⋅∥x∥+bt∥b∥時終止;否則將在∥ATr∥?at∥A∥⋅∥r∥。
如果兩個容忍度都是10−6 ,最終的∥r∥將有6位精度。
lsmr的參數如下
lsmr(A, b, damp=0.0, atol=1e-06, btol=1e-06, conlim=100000000.0, maxiter=None, show=False, x0=None)
參數解釋:
A 可謂稀疏矩陣、數組以及線性算子
b 為數組
damp 阻尼系數,默認為0
atol, btol 截止容忍度,是lsqr迭代的停止條件,即at ,bt 。
conlim 另一個截止條件,對于最小二乘問題,conlim應該小于108,如果Ax=b是相容的,則conlim最大可以設到1012
iter_limint 迭代次數
show 如果為True,則打印運算過程
calc_var 是否估計(A.T@A + damp**2*I)^{-1}的對角線
x0 阻尼系數相關
lsqr和lsmr相比,沒有maxiter參數,但多了iter_lim, calc_va參數。
上述參數中,damp為阻尼系數,當其不為0時,記作δ,待解決的最小二乘問題變為

lsmr的返回值依次為:
x 即Ax=b中的x
istop 程序結束運行的原因
itn 迭代次數
normr ∥b−Ax∥
normar ∥AT (b−Ax)∥
norma ∥A∥
conda A的條件數
normx ∥x∥
lsqr的返回值為
x 即Ax=b中的x
istop 程序結束運行的原因
itn 迭代次數
r1norm 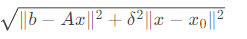
anorm 估計的Frobenius范數Aˉ
acond Aˉ的條件數
arnorm ∥ATr−δ2(x−x0)∥
xnorm ∥x∥
var (ATA)−1
二者的返回值較多,而且除了前四個之外,剩下的意義不同,調用時且須注意。
下面對這兩種算法進行驗證,第一步就得先有一個稀疏矩陣
import numpy as np from scipy.sparse import csr_array np.random.seed(42) # 設置隨機數狀態 mat = np.random.rand(500,500) mat[mat<0.9] = 0 csr = csr_array(mat)
然后用這個稀疏矩陣乘以一個x,得到b
xs = np.arange(500) b = mat @ xs
接下來對這兩個最小二乘函數進行測試
from scipy.sparse.linalg import lsmr, lsqr import matplotlib.pyplot as plt mx = lsmr(csr, b)[0] qx = lsqr(csr, b)[0] plt.plot(xs, lw=0.5) plt.plot(mx, lw=0, marker='*', label="lsmr") plt.plot(qx, lw=0, marker='.', label="lsqr") plt.legend() plt.show()
為了對比清晰,對圖像進行放大,可以說二者不分勝負
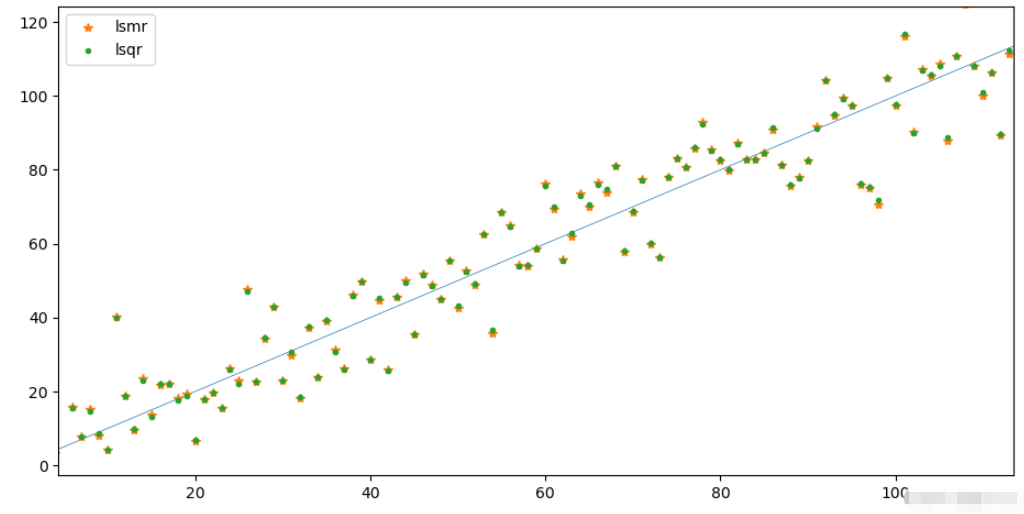
接下來比較二者的效率,500 × 500 500\times500500×500這個尺寸顯然已經不合適了,用2000×2000
from timeit import timeit np.random.seed(42) # 設置隨機數狀態 mat = np.random.rand(500,500) mat[mat<0.9] = 0 csr = csr_array(mat) timeit(lambda : lsmr(csr, b), number=10) timeit(lambda : lsqr(csr, b), number=10)
測試結果如下
>>> timeit(lambda : lsqr(csr, b), number=10)
0.5240591000001587
>>> timeit(lambda : lsmr(csr, b), number=10)
0.6156221000019286
看來lsmr并沒有更快,看來斯坦福也不靠譜(滑稽)。
以上就是“Python如何實現兩種稀疏矩陣的最小二乘法”這篇文章的所有內容,感謝各位的閱讀!相信大家閱讀完這篇文章都有很大的收獲,小編每天都會為大家更新不同的知識,如果還想學習更多的知識,請關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。