Java如何實現Kruskal算法

本文小編為大家詳細介紹“Java如何實現Kruskal算法”，內容詳細，步驟清晰，細節處理妥當，希望這篇“Java如何實現Kruskal算法”文章能幫助大家解決疑惑，下面跟著小編的思路慢慢深入，一起來學習新知識吧。

介紹

構造最小生成樹還有一種算法，即 Kruskal 算法：設圖 G=（V，E）是無向連通帶權圖，V={1,2，...n};設最小生成樹 T=(V，TE)，該樹的初始狀態只有 n 個節點而無邊的非連通圖T=(V,{}),Kruskal 算法將這n 個節點看成 n 個孤立的連通分支。它首先將所有邊都按權值從小到大排序，然后值要在 T 中選的邊數不到 n-1,就做這樣貪心選擇：在邊集 E 中選擇權值最小的邊(i,j),如果將邊(i,j)加入集合 TE 中不產生回路，則將邊(i,j)加入邊集 TE 中，即用邊(i，j)將這兩個分支合并成一個連通分支；否則繼續選擇下一條最短邊。把邊(i,j)從集合 E 中刪去，繼續上面的貪心選擇，直到 T 中的所有節點都在同一個連通分支上為止。此時，選取的 n-1 條邊恰好構成圖 G 的一棵最小生成樹 T。

Kruskal 算法用一種非常聰明的方法，就是運用集合避圈；如果所選擇加入邊的起點和終點都在 T 集合中，就可以斷定會形成回路，變的兩個節點不能屬于同一個集合。

算法步驟

1 初始化。將所有邊都按權值從小到大排序，將每個節點集合號都初始化為自身編號。

2 按排序后的順序選擇權值最小的邊（u,v）。

3 如果節點 u 和 v 屬于兩個不同的連通分支，則將邊(u,v)加入邊集 TE 中，并將兩個連通分支合并。

4 如果選取的邊數小于 n-1,則轉向步驟2，否則算法結束。

一、構建后的圖

二、代碼

package graph.kruskal;
 
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Scanner;
 
public class Kruskal {
    static final int N = 100;
    static int fa[] = new int[N];
    static int n;
    static int m;
 
    static Edge e[] = new Edge[N * N];
    static List<Edge> edgeList = new ArrayList();
 
    static {
        for (int i = 0; i < e.length; i++) {
            e[i] = new Edge();
        }
    }
 
    // 初始化集合號為自身
    static void Init(int n) {
        for (int i = 1; i <= n; i++)
            fa[i] = i;
    }
 
    // 合并
    static int Merge(int a, int b) {
        int p = fa[a];
        int q = fa[b];
        if (p == q) return 0;
        for (int i = 1; i <= n; i++) { // 檢查所有結點，把集合號是 q 的改為 p
            if (fa[i] == q)
                fa[i] = p; // a 的集合號賦值給 b 集合號
        }
        return 1;
    }
 
    // 求最小生成樹
    static int Kruskal(int n) {
        int ans = 0;
        Collections.sort(edgeList);
        for (int i = 0; i < m; i++)
            if (Merge(edgeList.get(i).u, edgeList.get(i).v) == 1) {
                ans += edgeList.get(i).w;
                n--;
                if (n == 1)//n-1次合并算法結束
                    return ans;
            }
        return 0;
    }
 
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        m = scanner.nextInt();
        Init(n);
        for (int i = 1; i <= m; i++) {
            e[i].u = scanner.nextInt();
            e[i].v = scanner.nextInt();
            e[i].w = scanner.nextInt();
            edgeList.add(e[i]);
        }
        System.out.println("最小的花費是：" + Kruskal(n));
    }
}
 
class Edge implements Comparable {
    int u;
    int w;
    int v;
 
    @Override
    public int compareTo(Object o) {
        if (this.w > ((Edge) o).w) {
            return 1;
        } else if (this.w == ((Edge) o).w) {
            return 0;
        } else {
            return -1;
        }
    }
}

三、測試

綠色為輸入，白色為輸出。

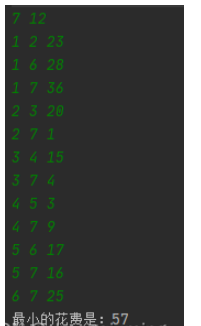
讀到這里，這篇“Java如何實現Kruskal算法”文章已經介紹完畢，想要掌握這篇文章的知識點還需要大家自己動手實踐使用過才能領會，如果想了解更多相關內容的文章，歡迎關注億速云行業資訊頻道。