您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“C++如何實現優先隊列”的相關知識,小編通過實際案例向大家展示操作過程,操作方法簡單快捷,實用性強,希望這篇“C++如何實現優先隊列”文章能幫助大家解決問題。
首先,啊,先簡單介紹一下優先隊列的概念,學數據結構以及出入算法競賽的相信都對隊列這一數據結構十分熟悉,這是一個線性的數據結構.
針對隊列這一特殊數據結構,有時需考慮隊列元素的優先級的關系,即根據用戶自定義的優先級排序,出隊時優先彈出優先級更高(低)的元素,優先隊列能更好地滿足實際問題中的需求,而在優先隊列的各種實現中,堆是一種最高效的數據結構。
什么是堆
堆是一顆具有特定性質的二叉樹,堆的基本要求就是堆中所有結點的值必須大于或等于(或小于或等于)其孩子結點的值,這也稱為堆的性質,我們也叫堆序性;堆還有另一個性質,就是當 h > 0 時,所有葉子結點都處于第 h 或 h - 1 層(其中 h 為樹的高度,完全二叉樹),也就是說,堆應該是一顆完全二叉樹;
如下:
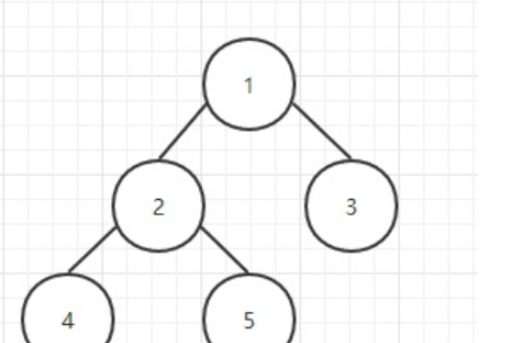
根據兩種堆序性,我們將堆分為兩類,即根節點權值≥子節點權值的我們叫大根堆,根節點權值≤子節點權值的我們叫小根堆。道理簡單,就不做圖演示了。
上文所述,優先隊列是由一個堆維護的,堆序性正對應了優先隊列的優先級。由此,優先隊列就并不是一個線性的數據結構,其所有操作都是logn的時間復雜度。
了解完堆與優先隊列的關系,我們就可以開始討論如何實現優先對列了。
我們將一個堆從上到下從左到右(實際上這個順序也是堆一般的討論模式),從0開始給每個節點編號。如下圖:
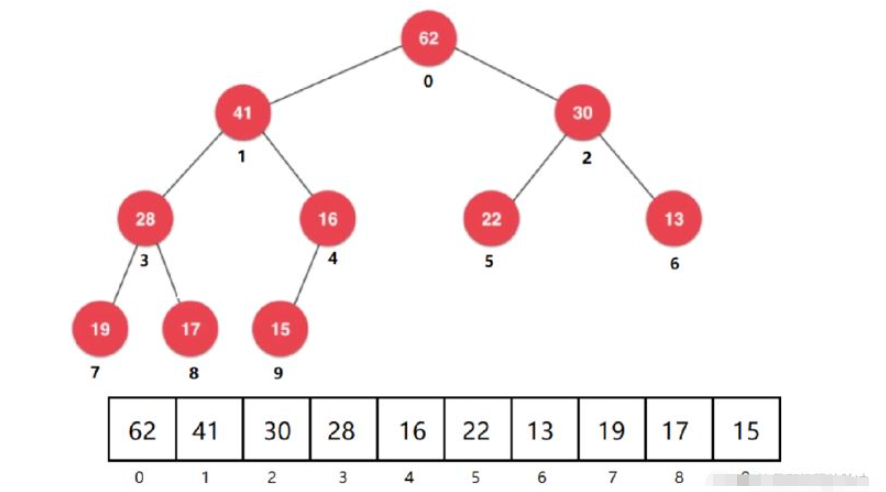
然后按照順序存儲進一個線性的數組之中,那么這就算存儲好了~
簡不簡單?意不意外?是不是最開始想到的是遞歸生成樹?但實際上因為堆序性的存在,我們并不需要那么復雜的存儲方式~
同樣的道理,我們反過來用一個數組建堆,也就是如上操作的逆操作而已。
問題就來了,如何用一個無序的數組來建堆呢?這就要談到維護堆序性的兩種操作——上浮,下沉。
首先將一個無序的數組按下標標號,然后開始進行前方所說的建堆操作,我們建堆的過程便是主要用到上浮操作,每操作一步就要與父節點比較,如果大于(此處以大根堆為例子)父節點,則與父節點進行交換,然后跳轉到交換后的位置,繼續與父節點進行比較,直到不大于父節點后,就算完成了一次調整。光說肯定有些童鞋無法想象得那么明白,下面放圖!
這里用數組a[6] = {3,5,8,9,1,2}做模板,別多想,很隨機的數字罷了。
第一步,將下標為0的節點做根節點,就是3啦~
第二步,將下標為1的節點也就是5作為3的左孩子~

很明顯啊,5要比它的父節點3要大,那么,交換位置~
再看5并沒有比它小的根節點了,那么繼續下一步~
第三步,將下標為2的節點也就是8,放在5的下邊作為右孩子~
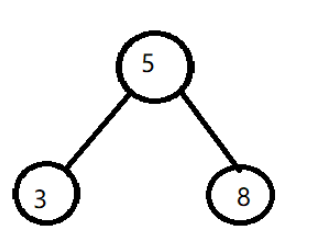
很明顯哦,8比它的父節點大,那么~,交換位置~
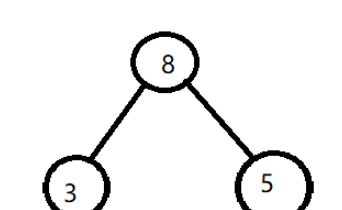
很明顯,8并沒有比它更小的父節點了,那么繼續下一步~
再接下去我就不講了,很簡單,序號從上到下從左到右。
那么任一的一個節點如果它足夠大(小),就一定會最底下一層爬到最大的根節點,是不是上浮呢,生動而形象,在建堆的時候每插入一個元素,就要對該元素進行一次上浮調整,將其放在正確的地方。
相信聰明的童鞋已經發現了,同層的節點不存在任何的關系!!!甚至不同根節點的同層節點也不存在任何關系,每一個節點僅僅只是在其子堆中的最大值,即局部最大值。
該操作在隊列的基本操作,也就是彈出隊頂操作時所用,即刪除最大(小)根節點的操作。
原理也很簡單,將編號為0的節點與編號最大的節點權值互換,然后彈出編號最大的節點(此時即前一步的隊頂元素),此時再對隊頂節點進行下沉操作:
先與左子樹進行比較,按照堆序性交換,直到換回它應在的位置,此時所有局部均為優先隊列,其也維護完成。
上圖:
這里還是前面那個數組,順便也給大家看看建堆后的亞子~
a[6] = {3,5,8,9,1,2}

第一步, 將編號為0的節點與編號最大的節點權值互換
即將9與2進行互換。
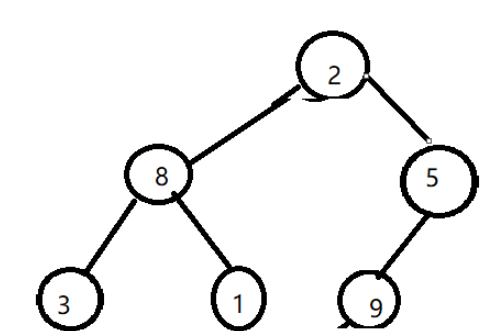
第二步, 彈出編號最大的節點(此時即前一步的隊頂元素)
即9
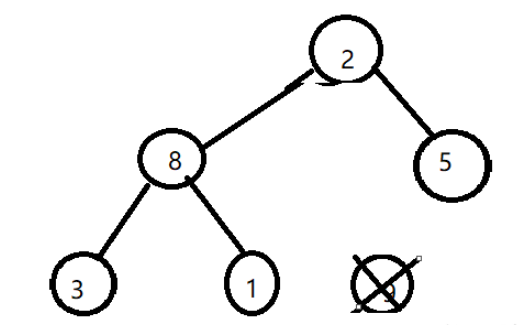
第三步, 對隊頂節點進行下沉操作
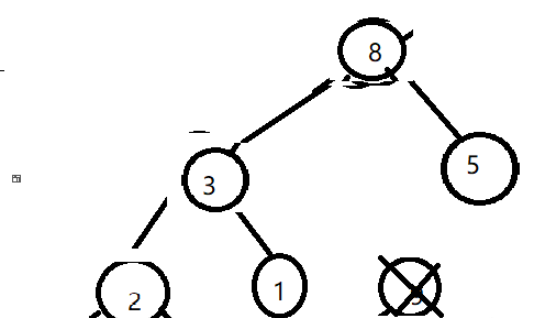
即先和8,5進行順序比較,按照優先級,明顯與8互換,換完后如下
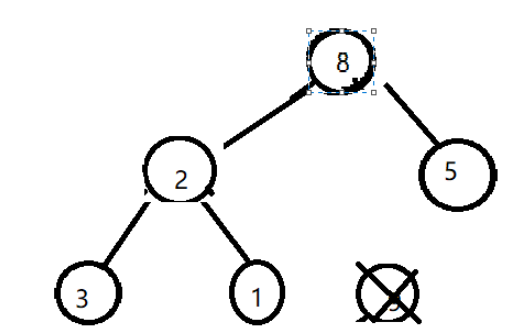
再與3先比較,無法交換再與1比較~最后應該是這個樣子的。
兩種操作方式也已經說完,這里就會有童鞋問道,那么如何在數組中進行所謂的上浮下沉,操作呢?
這里就有一個很重要的知識了,就是父節點和子節點在數組編號中的關系!
其實也并不難發現,根據堆的性質,有如下的關系:
設某個節點編號為i:
其父節點:dad = (i - 1) / 2
左/右子節點:left = 2 * i + 1
right = 2 * i + 2
這樣大家就可以將上浮、下沉操作的每一步在數組中實現了!
#include<iostream>
#include<cmath>
#include<stdlib.h>
#define bug cout<<"nug is here"<<endl;
#include<vector>
using namespace std;
typedef size_t ull;
//堆
template<typename P>
class Heap{
private:
vector<int> heap_elem;//堆容器
ull heap_depth;//深度
bool Priority; //優先級
ull heap_size; //容量
void Up_adjust(int now);//上浮調整
void Down_adjust(int now);//下沉調整
//now指代下標
public:
//構造堆
enum{max_heap = true, min_heap = false};
Heap(vector<P> &l, bool priority = max_heap){
heap_size = l.size();
heap_depth = log2(heap_size);
Priority = priority;//設置優先級
for(int i = 0;i < heap_size;i++){
heap_elem.push_back(l[i]);
Up_adjust(i);//上浮調整
}
}
Heap(int a[], ull n, bool priority = max_heap){
heap_size = n;
heap_depth = log2(heap_size);
Priority = priority;//設置優先級
for(int i = 0;i < n;i++){
heap_elem.push_back(a[i]);
Up_adjust(i);//上浮調整
}
}
Heap(){
heap_size = 0;
heap_depth = 0;
Priority = max_heap;
};
//堆的成員函數
ull Depth(){
return heap_depth;
}
ull Size(){
return heap_size;
}
void Push(P x){
heap_elem.push_back(x);
++heap_size;
heap_depth = log2(heap_size);
swap(heap_elem[heap_elem.size() - 1], heap_elem[heap_size - 1]);//將加入的元素放入有效位
Up_adjust(heap_size - 1);
}
void Pop(){
heap_depth = log2(heap_size);
swap(heap_elem[--heap_size], heap_elem[0]);//將第一個元素與最后一個元素交換,并且縮短有效位數
//其實這里可以用vector的函數pop_back(),相應的上面的Push函數也不用換位置,但是這樣更快
Down_adjust(0);
}
P &Top(){
return heap_elem[0];
}
void show_as_tree(){//以樹的形式輸出
int _size = max(log10(heap_elem[0]),log10(heap_elem[heap_size - 1])) + 1;
ull max_size = (pow(2, heap_depth) * 2) * _size;
ull _max_size = _size * pow(2, heap_depth + 1);
int start = -1;
for(int i = 0;i <= heap_depth;i++){
max_size >>= 1;
max_size++;
if(i == heap_depth) cout<<heap_elem[++start];
else printf("%*d",max_size,heap_elem[++start]);
int w = pow(2, i);
for(int j = 1;j < w && start < heap_size - 1;j++) printf("%*d",_max_size,heap_elem[++start]);
_max_size >>= 1;
_max_size++;
printf("\n");
}
}
void show_as_array(){//數組方式輸出
for(int i = 0;i < heap_size;i++) cout<<heap_elem[i]<<" ";
cout<<endl;
}
};
//上浮調整
template<typename P>
void Heap<P>::Up_adjust(int now){
if(Priority)
while(now > 0 && heap_elem[now] > heap_elem[(now - 1) / 2]){//如果當前節點的權值比父親大
swap(heap_elem[now], heap_elem[(now - 1) / 2]);//交換
now = (now - 1) / 2;
}
else
while(now > 0 && heap_elem[now] < heap_elem[(now - 1) / 2]){
swap(heap_elem[now], heap_elem[(now - 1) / 2]);
now = (now - 1) / 2;
}
}
//下沉調整
template<typename P>
void Heap<P>::Down_adjust(int now){
ull left = now * 2 + 1;
ull right;
while(left < heap_size){//能換的時候
left = now * 2 + 1;
right = now * 2 + 2;
if(Priority){
if(heap_elem[now] < heap_elem[left]){//比左孩子小,下沉
swap(heap_elem[now], heap_elem[left]);
now = left;
}
else if(right < heap_size){//比右孩子小,下沉
if(heap_elem[now] > heap_elem[right]){
swap(heap_elem[now], heap_elem[right]);
now = right;
}
}
}
else{
if(heap_elem[now] > heap_elem[left]){//比左孩子大,下沉
swap(heap_elem[now], heap_elem[left]);
now = left;
}
else if(right > heap_size){//比右孩子大,下沉
if(heap_elem[now] < heap_elem[right]){
swap(heap_elem[now], heap_elem[right]);
now = right;
}
}
}
}
}
int main(){
int a[6] = {3,5,8,9,1,2};
Heap<int> h(a, 6, true);
//輸出堆
h.show_as_tree();
// h.Push(12);
// h.show_as_tree();
//
// h.Pop();
// h.show_as_tree();
//
// cout<<h.Top()<<endl;
// vector<int> a;
// Heap<int> h(a, Heap<int>::max_heap);
// for(int i=0;i < 10;++i)
// h.Push(rand()%100);
//
// h.show_as_tree();
return 0;
}按照前面那個數組運行,結果如下:

關于“C++如何實現優先隊列”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識,可以關注億速云行業資訊頻道,小編每天都會為大家更新不同的知識點。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。