您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容介紹了“C#怎么利用遞歸算法解決漢諾塔問題”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!
方法調用自己的行為就是遞歸,遞歸必須要有終止條件,不然它會無限遞歸。
1.先來看一下一個遞歸的例子
此程序的Fact方法從大到小地一級一級地調用自己,直到參數為1,然后就開始返回一級一級的從小到大地累乘,然后就計算出number的階乘了。
static int Fact(int num)
{
if (num <= 1)
{
return num;
}
else
{
return num * Fact(num - 1);//調用自己,這一步是關鍵
}
}2.遞歸的基本原理
以下是《C#圖解教程》對于遞歸的描述:
除了調用其他方法,方法也可以調用自身,這叫做遞歸。
調用方法自身的機制和調用其他方法其實是完全一樣的,都是為每一次方法調用把新的棧幀壓入棧頂。
我個人認為遞歸就是把你要干的事情抽象一個成可以有限步數解決的方法,然后某一步解決不了就再調用這個方法,直到可以解決(結束遞歸的條件)這個問題就返回。
下面再看一個具體的例子來了解遞歸。
漢諾塔由法國數學家愛德華·盧卡斯創造,他曾經編寫了一個印度的古老傳說:
在世界中心貝拿勒斯(在印度北部)的圣廟里,一塊黃銅板上插著三根寶石針。印度教的主神梵天在創造世界的時候,在其中一根針上從下到上地穿好了由大到小的64片金片,這就是所謂的漢諾塔。不論白天黑夜,總有一個僧侶在按照下面的法則移動這些金片:一次只移動一片,不管在哪根針上,小片必須在大片上面。僧侶們預言,當所有的金片都從梵天穿好的那根針上移到另外一根針上時,世界就將在一聲霹靂中消滅,而梵塔、廟宇和眾生也都將同歸于盡。
回到編程,漢諾塔問題主要就是解決這個問題:
有A、B、C三根針,A上從小到大放著n層盤子,要從A上所有的盤子移動到C盤上。
條件是一次只能移動一個盤子,無論什么時候小盤子必須在大盤子上面。
漢諾塔問題求的是把盤子從A移到C總共的移動次數是多少。
這是我之前追蹤4層漢諾塔運行步驟畫的筆記

事實證明,沒多大幫助。
要想理解遞歸必須要放棄理解遞歸,放棄跟蹤全程步驟。
解決問題是計算機的事,你只要明確要把每一步怎么傳給計算機,遞歸兩層之間怎么交接,以及遞歸結束的條件就可以。
要解決漢諾塔問題就要用到遞歸思想,這里拿四層漢諾塔舉例子:
要完成四層漢諾塔,需要先把第四層盤子從A柱放到C柱,而要把第四層盤子放到C柱,就要把上面三層的盤子放到B柱:

那么要把這三層盤子移到B柱,那么就要先把第三層盤子移到B柱。
要把第三層盤子移到B柱,就要把第二層盤子移到C柱子。
要把第二層盤子移到C柱,就要把第一層盤子移到B柱子。
移動一層漢諾塔到另一個柱不簡單嗎?
這樣子把問題解決了,第四層盤子就可以移動到C柱上了。
然后把剩下的三層漢諾塔也按照上面的思想,就可以移動到C柱上了。
視頻鏈接
把大象裝進冰箱需要多少步
把冰箱門打開
把大象放進去
把冰箱門關上
把漢諾塔放到C柱需要多少步
把底層上面的盤子放到B柱
把最底層盤子放到C柱
把B柱那些盤子放到C柱
抽象一下就是:
把n-1層盤子從起點移到暫存區
然后把第n層盤子從起點移到終點
然后把n-1層盤子從暫存區移到終點
在這里可以創建一個Move方法來移動盤子
static void Move(int pile, char src, char tmp, char dst)
{
}src就是源起點,tmp就是暫存區,dst就是終點
最外層的Move方法完成的是把pile層漢諾塔從src經過tmp移動到dst
現在要把大象裝進冰箱了
在Move方法里面調用Move方法來解決之后的問題:
1. 把冰箱門打開
Move(pile - 1, src, dst, tmp);
這層Move完成的是把pile-1層漢諾塔從src經過dst移動到tmp
2.把大象塞進去
Move(1, src, tmp, dst);
這層Move完成的是把最底層漢諾塔盤子從src直接移動到dst
3.把門關上
Move(pile - 1, tmp, src, dst);
這層Move完成的是把pile-1層漢諾塔從tmp經過src移動到dst
Move方法完整代碼:
static void Move(int pile, char src, char tmp, char dst)
{
if (pile == 1)//pile=1問題就好解決了
{
Console.WriteLine($"{src} --> {dst}");
steps++;
return;
}
Move(pile - 1, src, dst, tmp);
Move(1, src, tmp, dst);
Move(pile - 1, tmp, src, dst);
}每一層Move方法都有他自己的起點、暫存區和終點,我們只需要把上一層的起點、暫存區和終點傳過去就行了。
以下是完整代碼:
using System;
namespace Hanoi
{
class Program
{
public const int MAX_VALUE = 30;//聲明最大值常量
public static int steps = 0;
static void Main(string[] args)
{
int levels = 0;
Console.Write($"輸入漢諾塔層數(1~{MAX_VALUE}): ");
levels = int.Parse(Console.ReadLine());
if (levels > 0 && levels < MAX_VALUE)
{
Move(levels, 'A', 'B', 'C');
Console.WriteLine($"一共移動了{Program.steps}次。");
Console.ReadKey();
return;
}
Console.WriteLine("輸入范圍錯誤");
Console.ReadKey();
}
static void Move(int pile, char src, char tmp, char dst)
{
if (pile == 1)//pile=1問題就好解決了
{
Console.WriteLine($"{src} --> {dst}");
steps++;
return;
}
Move(pile - 1, src, dst, tmp);
Move(1, src, tmp, dst);
Move(pile - 1, tmp, src, dst);
}
}
}運行結果如下:
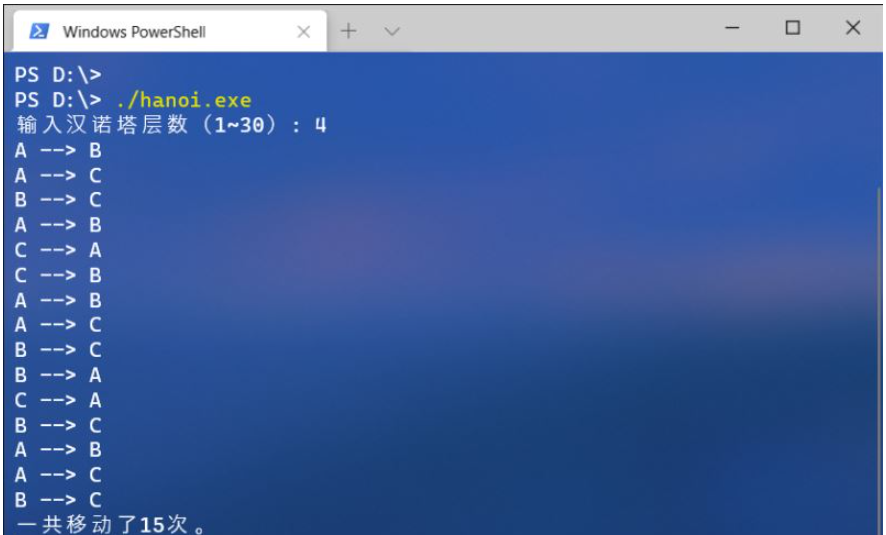
“C#怎么利用遞歸算法解決漢諾塔問題”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站,小編將為大家輸出更多高質量的實用文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。