您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容主要講解“C語言二叉樹的概念是什么及怎么使用”,感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷,實用性強。下面就讓小編來帶大家學習“C語言二叉樹的概念是什么及怎么使用”吧!
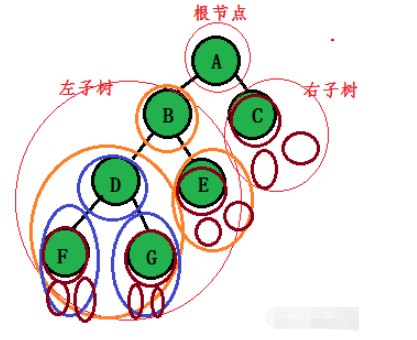
①概念:一棵二叉樹是結點的一個有限集合,該集合或者為空,或者是由一個根節點加上兩棵別稱為左子樹和右子樹的二叉樹組成。
②二叉樹的特點:
每個結點最多有兩棵子樹,即二叉樹不存在度大于2的結點。(度最多為2)
二叉樹的子樹有左右之分,其子樹的次序不能顛倒。
③現實中的二叉樹:

當一名普通的人看到這樣一顆樹,可能會想:好標準的一棵樹
當一個程序猿看到這樣一棵樹,可能會想:好像數據結構中的二叉樹,并且還是顆滿二叉樹
④數據結構中的二叉樹:
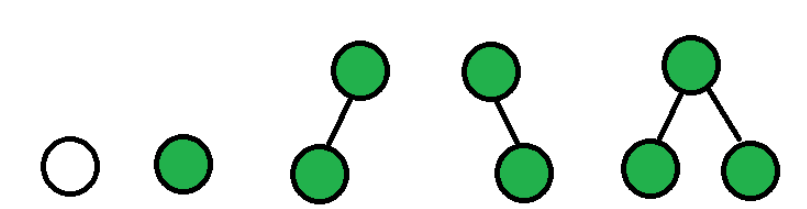
注:二叉樹最多有兩個度
⑤特殊的二叉樹:
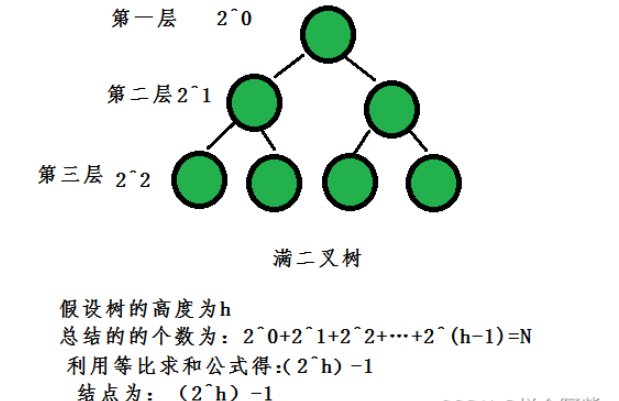
滿二叉樹:一個二叉樹,如果每一個層的結點數都達到最大值,則這個二叉樹就是滿二叉 樹。也就是說,如果一個二叉樹的層數為K,且結點總數是(2^k) -1 ,則它就是滿二叉樹。
完全二叉樹:完全二叉樹是效率很高的數據結構,完全二叉樹是由滿二叉樹而引出來的。對 于深度為K的,有n個結點的二叉樹,當且僅當其每一個結點都與深度為K的滿二叉樹中編號 從1至n的結點一一對應時稱之為完全二叉樹。 要注意的是滿二叉樹是一種特殊的完全二叉 樹。

⑥二叉樹的存儲結構: 二叉樹一般可以使用兩種結構存儲,一種順序結構,一種鏈式結構。
⑦二叉樹的性質:
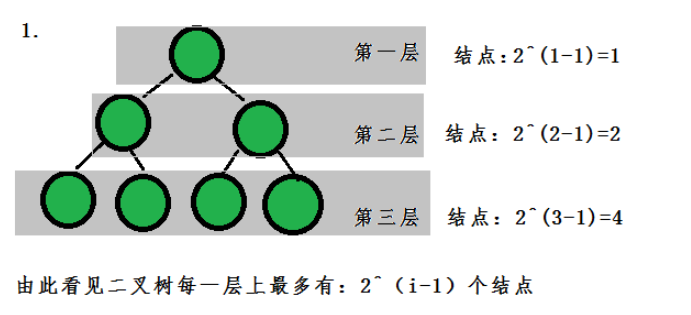
若規定根節點的層數為1,則一棵非空二叉樹的第i層上最多有2^(i-1) 個結點.
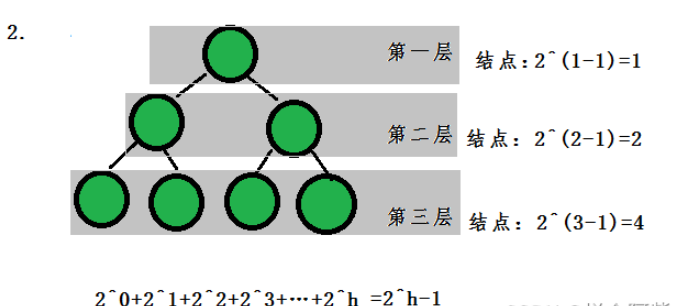
若規定根節點的層數為1,則深度為h的二叉樹的最大結點數是2^h- 1.
對任何一棵二叉樹, 如果度為0其葉結點個數為 n0, 度為2的分支結點個數為 n2,則有n0=n2 +1
若規定根節點的層數為1,具有n個結點的滿二叉樹的深度,h=log?n+1
⑧練習題


①二叉樹鏈式結構的遍歷 :
所謂遍歷(Traversal)是指沿著某條搜索路線,依次對樹中每個結點均做一次且僅做一次訪問。訪 問結點所做的操作依賴于具體的應用問 題。 遍歷是二叉樹上最重要的運算之一,是二叉樹上進行 其它運算之基礎。
前序/中序/后序的遞歸結構遍歷:是根據訪問結點操作發生位置命名
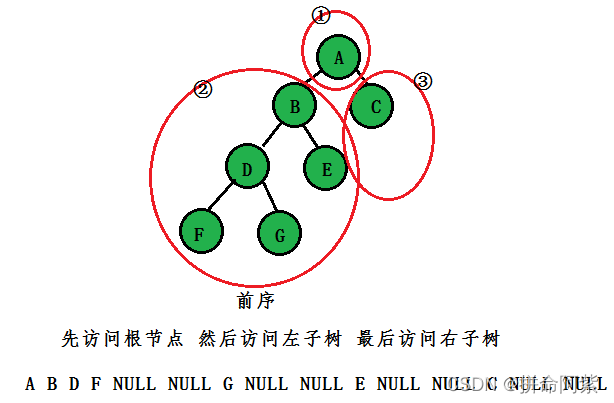
前序(先根):先訪問根節點,然后訪問左子樹,最后訪問右子樹
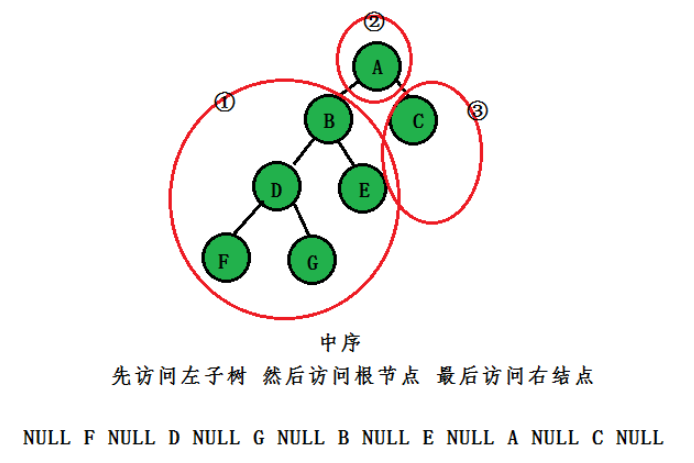
中序(中根):先訪問左節點,然后訪問根節點,最后訪問右子樹
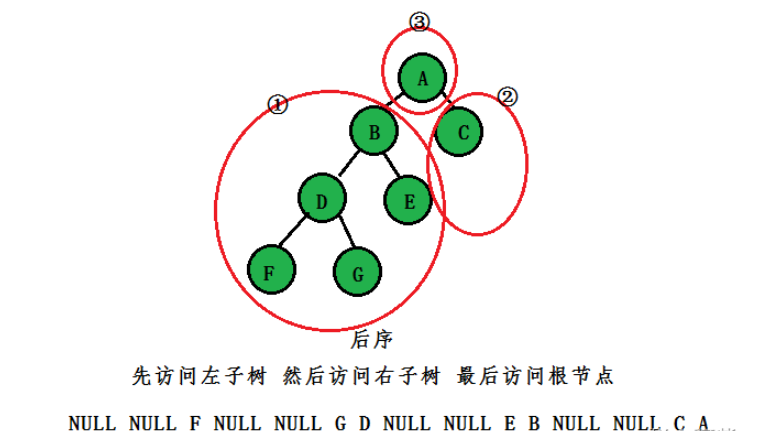
后序(后根):先訪問左節點,然后訪問右子樹,最后訪問根節點
先定一個結構體類型:
typedef char BTDataType;
typedef struct BinarytreeNode
{
BTDataType data;
struct BinarytreeNode* left;
struct BinarytreeNode* right;
}BTNode;前序:
void Preamble(BTNode* p)//前序
{
if (p == NULL)
{
printf("NULL ");
return;
}
printf("%c ", p->data);
Preamble(p->left);
Preamble(p->right);
}中序:
void Morder(BTNode* p)//中序
{
if (p == NULL)
{
printf("NULL ");
return;
}
Morder(p->left);
printf("%c ", p->data);
Morder(p->right);
}后序:
void Porder(BTNode* p)//后序
{
if (p == NULL)
{
printf("NULL ");
return;
}
Porder(p->left);
Porder(p->right);
printf("%c ", p->data);
}求二叉樹結點的個數:
int treeSize(BTNode* p)//結點個數
{
return p == NULL ? 0 : treeSize(p->left) + treeSize(p->right)+1;
}求葉子結點的個數:
int treeLeafSize(BTNode* p)//葉子結點個數
{
if (p == NULL)
{
return 0;
}
if (p->left == NULL&&p->right == NULL)
{
return 1;
}
return treeLeafSize(p->left) + treeLeafSize(p->right);
}到此,相信大家對“C語言二叉樹的概念是什么及怎么使用”有了更深的了解,不妨來實際操作一番吧!這里是億速云網站,更多相關內容可以進入相關頻道進行查詢,關注我們,繼續學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。