您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
小編給大家分享一下C++回溯算法深度優先搜索的示例分析,希望大家閱讀完這篇文章之后都有所收獲,下面讓我們一起去探討吧!
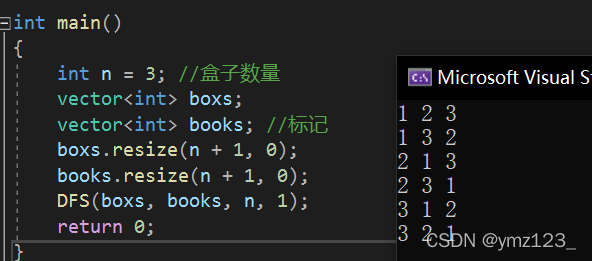
假如有編號為1~ 3的3張撲克牌和編號為1~3的3個盒子,現在需要將3張牌分別放到3個盒子中去,且每個盒子只能放一張牌,一共有多少種不同的放法。
解題思路:假定按照牌面值從小到大依次嘗試,即將1號牌放入第一個盒子中。按此順序繼續向后走,放完第三個盒子時,手中的牌也已經用完,再繼續往后則到了盒子的盡頭。此時一種放法已經完成了,即這條路走到了盡頭,需要折返,重新回到上一個盒子。這里回到第三個盒子,把第三個盒子中的牌回收,再去嘗試能否放其它的牌。但這時手里只有一張3號牌,所以需要繼續向后回退,到2號盒子。按照上述步驟依次會產生所有結果。 用一個數組book標記手里是否有這張牌。
Dfs(當前這一步的處理邏輯)
{
1. 判斷邊界,是否已經一條道走到黑了:向上回退
2. 嘗試當下的每一種可能
3. 確定一種可能之后,繼續下一步 Dfs(下一步)
}
代碼實現:
void DFS(vector<int>& boxs, vector<int>& books, int n, int index)
{
if (index >= n + 1)
{
for (int i = 1; i <= n; i++)
cout << boxs[i] << " "; //打印每一種結果
cout << endl;
return;
}
for (int i = 1; i <= n; i++)
{
if (books[i] == 0) //如果i號牌仍在手上
{
boxs[index] = i;
books[i] = 1;
DFS(boxs, books, n, index + 1);
books[i] = 0;
}
}
}
問題描述:
給定一個保存員工信息的數據結構,它包含了員工 唯一的 id ,重要度 和 直系下屬的 id 。 比如,員工 1 是員工 2 的領導,員工 2 是員工 3 的領導。他們相應的重要度為 15 , 10 , 5 。那么員工 1 的數據結構是 [1, 15, [2]] ,員工 2的 數據結構是 [2, 10, [3]] ,員工 3 的數據結構是 [3, 5, []] 。注意雖然員工 3 也是員工 1 的一個下屬,但是由于 并不是直系 下屬,因此沒有體現在員工 1 的數據結構中。
現在輸入一個公司的所有員工信息,以及單個員工 id ,返回這個員工和他所有下屬的重要度之和。
解題思路:
邊界:下屬為空
每次先加第一個下屬的重要性
按照相同的操作再去加下屬的第一個下屬的重要性。
代碼實現:
/*
// Definition for Employee.
class Employee {
public:
int id;
int importance;
vector<int> subordinates;
};
*/
class Solution {
public:
int DFS(unordered_map<int, Employee*>& info, int id)
{
int curImpo = info[id]->importance;
for(const auto& sid : info[id]->subordinates)
{
curImpo += DFS(info, sid);
}
return curImpo;
}
int getImportance(vector<Employee*> employees, int id) {
if(employees.empty())
return 0;
unordered_map<int, Employee*> info;
for(const auto& e : employees)
{
info[e->id] = e;
}
return DFS(info, id);
}
};問題描述:
有一幅以二維整數數組表示的圖畫,每一個整數表示該圖畫的像素值大小,數值在 0 到 65535 之間。 給你一個坐標 (sr, sc) 表示圖像渲染開始的像素值(行 ,列)和一個新的顏色值 newColor,讓你重新上色這幅圖像。 為了完成上色工作,從初始坐標開始,記錄初始坐標的上下左右四個方向上像素值與初始坐標相同的相連像素點,接著再記錄這四個方向上符合條件的像素點與他們對應四個方向上像素值與初始坐標相同的相連像素點,……,重復該過程。將所有有記錄的像素點的顏色值改為新的顏色值。
最后返回經過上色渲染后的圖像。
解題思路:
從所給坐標開始,向上下左右四個方向渲染,只要渲染點的顏色值和原坐標相同,則繼續向外渲染。 邊界:位置是否越界。
這里需要用標記避免重復修改,使時間復雜度不超過O(row*col)

代碼實現:
int nextP[4][2] = {{-1, 0}, {1, 0}, {0, 1}, {0, -1}};
class Solution {
public:
void DFS(vector<vector<int>>& image, vector<vector<int>>& book, int sr, int sc, int newColor, int oldColor, int row, int col)
{
image[sr][sc] = newColor;
book[sr][sc] = 1;
for(int i = 0; i < 4; i++)
{
int curX = sr + nextP[i][0];
int curY = sc + nextP[i][1];
//判斷是否越界
if(curX < 0 || curX >= row || curY < 0 || curY >= col)
continue;
//顏色符合要求且之前沒被渲染過則繼續渲染
if(image[curX][curY] == oldColor && book[curX][curY] == 0)
{
DFS(image, book, curX, curY, newColor, oldColor, row, col);
}
}
}
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int newColor) {
int row = image.size();
int col = image[0].size();
int oldColor = image[sr][sc];
vector<vector<int>> book(row, vector<int>(col, 0));
DFS(image, book, sr, sc, newColor, oldColor, row, col);
return image;
}
};問題描述:
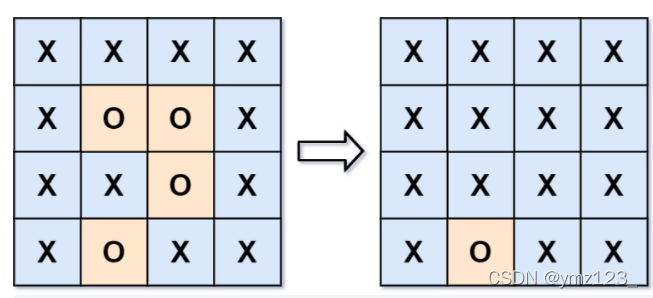
給你一個 m x n 的矩陣 board ,由若干字符 ‘X' 和 ‘O' ,找到所有被 ‘X' 圍繞的區域,并將這些區域里所有的 ‘O' 用 ‘X' 填充。
解題思路: 從每個邊緣的O開始,只要和邊緣的O連通,則它就沒有被包圍。
1.首先尋找邊上的每一個O,如果沒有,表示所有的O都被包圍。
2.對于邊上的每一個O進行dfs擴散,先把邊上的每一個O用特殊符號標記(除了X和O以外)。把和它相鄰的O都替換為特殊符號,每一個新的位置都做相同的dfs操作。
3.所有擴散結束之后,把特殊符號的位置(和邊界連通)還原為O,原來為O的位置(和邊界不連通)替換為X即可。
代碼實現:
int nextP[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
class Solution {
public:
void DFS(vector<vector<char>>& board, int curX, int curY, int row, int col)
{
board[curX][curY] = 'A';
for(int i = 0; i < 4; i++)
{
int x = curX + nextP[i][0];
int y = curY + nextP[i][1];
if(x < 0 || x >= row
||y < 0 || y >= col)
continue;
if(board[x][y] != 'A' && board[x][y] != 'X')
DFS(board, x, y, row, col);
}
}
void solve(vector<vector<char>>& board) {
if(board.empty())
return;
int row = board.size();
int col = board[0].size();
//第一行和最后一行
for(int i = 0; i < col; i++)
{
if(board[0][i] == 'O')
DFS(board, 0, i, row, col);
if(board[row-1][i] == 'O')
DFS(board, row-1, i, row, col);
}
//第一列和最后一列
for(int i = 0; i < row; i++)
{
if(board[i][0] == 'O')
DFS(board, i, 0, row, col);
if(board[i][col-1] == 'O')
DFS(board, i, col-1, row, col);
}
for(int i = 1; i < row-1; i++)
{
for(int j = 0; j < col; j++)
{
if(board[i][j] == 'A')
board[i][j] = 'O';
else if(board[i][j] == 'O')
board[i][j] = 'X';
}
}
}
};問題描述:
給你一個由 ‘1'(陸地)和 ‘0'(水)組成的的二維網格,請你計算網格中島嶼的數量。 島嶼總是被水包圍,并且每座島嶼只能由水平方向和/或豎直方向上相鄰的陸地連接形成。 此外,你可以假設該網格的四條邊均被水包圍。
示例 1:
輸入:grid = [ [“1”,“1”,“1”,“1”,“0”], [“1”,“1”,“0”,“1”,“0”], [“1”,“1”,“0”,“0”,“0”], [“0”,“0”,“0”,“0”,“0”] ]
輸出:1
解題思路:
本題可以采用類似渲染的做法,嘗試以每個點作為渲染的起點,可以渲染的陸地都算作一個島嶼,最后看渲染了多少次,即深度優先算法執行了多少次,就是島嶼的數量。
代碼實現:
int nextP[4][2] = { { 0, 1 }, { 1, 0 }, { 0, -1 }, { -1, 0 } };
class Solution {
public:
void DFS(vector<vector<char>>& grid, vector<vector<int>>& book, int x, int y, int row, int col)
{
book[x][y] = 1;
for(int i = 0; i < 4; i++)
{
int curX = x + nextP[i][0];
int curY = y + nextP[i][1];
if(curX < 0 || curX >= row || curY < 0 || curY >= col)
continue;
if(grid[curX][curY] == '1' && book[curX][curY] == 0)
DFS(grid, book, curX, curY, row, col);
}
}
int numIslands(vector<vector<char>>& grid) {
if(grid.empty())
return 0;
int row = grid.size();
int col = grid[0].size();
int num = 0;
vector<vector<int>> book(row, vector<int>(col, 0));
for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
if(grid[i][j] == '1' && book[i][j] == 0)
{
++num;
DFS(grid, book, i, j, row, col);
}
}
}
return num;
}
};問題描述:
給定一個僅包含數字 2-9 的字符串,返回所有它能表示的字母組合。答案可以按 任意順序 返回。 給出數字到字母的映射如下(與電話按鍵相同)。注意 1 不對應任何字母。

解題思路:
首先使用數組(也可使用哈希表)存儲每個數字對應的所有可能的字母,然后進行回溯操作。回溯算法用于尋找所有的可行解,如果發現一個解不可行,則會舍棄不可行的解。在這道題中,由于每個數字對應的每個字母都可能進入字母組合,因此不存在不可行的解,直接窮舉所有的解即可。
代碼實現:
string mapString[] = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
class Solution {
public:
void DFS(string& digits, vector<string>& result, string curStr, int curDepth)
{
//邊界,找到一種組合,放入數組中,結束此路徑,向上回溯
if(curDepth == digits.size())
{
if(!curStr.empty())
result.push_back(curStr);
return;
}
//找到當前字符映射在mapString種的位置
int curMapIndex = digits[curDepth] - '0';
string curMap = mapString[curMapIndex];
//遍歷每一種可能
for(const auto& ch : curMap)
{
DFS(digits, result, curStr+ch, curDepth+1);
}
}
vector<string> letterCombinations(string digits) {
vector<string> result;
DFS(digits, result, "", 0);
return result;
}
};問題描述:
給你一個 無重復元素 的整數數組 candidates 和一個目標整數 target ,找出 candidates 中可以使數字和為目標數 target 的 所有不同組合 ,并以列表形式返回。你可以按 任意順序 返回這些組合。
candidates 中的 同一個 數字可以 無限制重復被選取 。如果至少一個數字的被選數量不同,則兩種組合是不同的。
對于給定的輸入,保證和為 target 的不同組合數少于 150 個。
輸入:candidates = [2,3,6,7], target = 7
輸出:[[2,2,3],[7]]
解題思路:
此題相加的元素可以重復,所以去下一個元素的位置可以從當前位置開始,DFS+回溯。為了保證組合不重復(順序不同,元素相同,也算重復),不再從當前位置向前看。
1.從第一個元素開始相加
2.讓局部和繼續累加候選的剩余值
3.局部和等于目標值,保存組合,向上回退,尋找其它組合
代碼實現:
class Solution {
public:
void DFS(vector<int>& candidates, vector<vector<int>>& result, vector<int> curCand, int prePos, int curSum, int target)
{
if(curSum >= target)
{
if(curSum == target)
result.push_back(curCand);
return;
}
for(int i = prePos; i < candidates.size(); i++)
{
if(candidates[i] <= target)
{
curCand.push_back(candidates[i]);
DFS(candidates, result, curCand, i, curSum+candidates[i], target);
//回溯
curCand.pop_back();
}
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<int>> result;
vector<int> curCand;
DFS(candidates, result, curCand, 0, 0, target);
return result;
}
};問題描述:
你有一套活字字模 tiles,其中每個字模上都刻有一個字母 tiles[i]。返回你可以印出的非空字母序列的數目。
注意:本題中,每個活字字模只能使用一次。
示例 1:
輸入:“AAB”
輸出:8
解釋:可能的序列為 “A”, “B”, “AA”, “AB”, “BA”, “AAB”, “ABA”, “BAA”。
解題思路:
此題組合的長度不唯一,最小組合長度為1,最大組合長度為tiles的長度。按照題意tiles中每一個位置的字符在組合中只能出現一次,所以可以用一個標記輔助。當組合新的組合時,可以與tiles種的每一個位置組合,但是如果當前位置已經在當前組合中出現過,則跳過。雖然此題種每一個位置的字符在組合中只能出現一次,但是tiles中可能有相同的字符,所以需要考慮重復的組合。而用unordered_set可以天然去重。
DFS+回溯:
1.當前組合不為空,則插入set中
2.繼續給當前組合拼接新的組合,嘗試拼接tiles每一個位置的字符
3.如果當前位置已經在組合中出現過,返回到2,否則標記當前位置,繼續拼接更長的組合
4.回溯,嘗試組合其它位置,返回2
當所有位置都已經使用過時,當前遞歸就結束了,繼續向上層DFS回退
最終返回set大小即為組合數目
代碼實現:
class Solution {
public:
void DFS(string& tiles, vector<int>& book, string curStr, unordered_set<string>& totolaString)
{
if(!curStr.empty())
{
totolaString.insert(curStr);
}
for(int i = 0; i < tiles.size(); i++)
{
//當前字符已用過,跳過
if(book[i] == 1)
continue;
book[i] = 1;
DFS(tiles, book, curStr+tiles[i], totolaString);
book[i] = 0;
}
}
int numTilePossibilities(string tiles) {
vector<int> book(tiles.size(), 0);
unordered_set<string> totolaString;
DFS(tiles, book, "", totolaString);
return totolaString.size();
}
};問題描述:
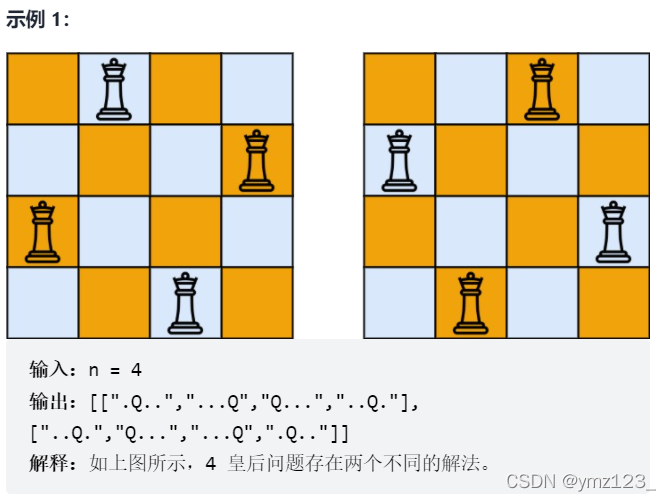
n 皇后問題 研究的是如何將 n 個皇后放置在 n×n 的棋盤上,并且使皇后彼此之間不能相互攻擊。
給你一個整數 n ,返回所有不同的 n 皇后問題 的解決方案。
每一種解法包含一個不同的 n 皇后問題 的棋子放置方案,該方案中 ‘Q' 和 ‘.' 分別代表了皇后和空位。
解題思路:
DFS+回溯
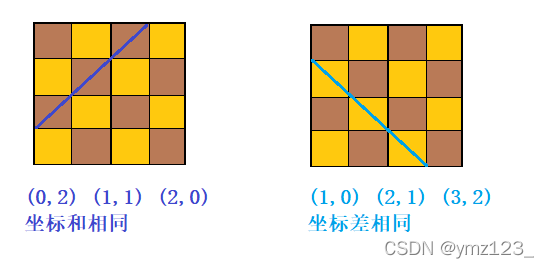
從第一行開始放置皇后,每確定一個位置,判斷是否會沖突(是否在同一列、同一斜線,已經不可能在同一行)
同一列:縱坐標相同
同一斜線:坐標差或坐標和相同。
當前行位置確定后,繼續確定下一行的位置。
回退,嘗試其他行的其它位置。
代碼實現:
class Solution {
public:
bool isValidPos(vector<pair<int, int>>& curRet, int row, int col)
{
for(pair<int, int> pos : curRet)
{
if(pos.second == col || pos.first + pos.second == row + col
|| pos.first - pos.second == row - col)
return false;
}
return true;
}
void DFS(vector<vector<pair<int, int>>>& allRet, vector<pair<int, int>>& curRet, int curRow, int n)
{
//如果每一行都沒有沖突,則是一種可行的方案
if(curRow == n)
{
allRet.push_back(curRet);
return;
}
//確定當前行的每一個位置是否和已確定的位置有沖突
for(int i = 0; i < n; i++)
{
if(isValidPos(curRet, curRow, i))
{
curRet.push_back(make_pair(curRow,i));
//處理下一行
DFS(allRet, curRet, curRow+1, n);
//回溯
curRet.pop_back();
}
}
}
vector<vector<string>> transResult(vector<vector<pair<int, int>>>& allRet, int n)
{
vector<vector<string>> allMap;
//所有方案
for(vector<pair<int, int>> curRet : allRet)
{
vector<string> curMap(n, string(n, '.'));
//一種方案中的所有皇后的位置
for(pair<int, int> pos : curRet)
{
curMap[pos.first][pos.second] = 'Q';
}
allMap.push_back(curMap);
}
return allMap;
}
vector<vector<string>> solveNQueens(int n) {
vector<vector<pair<int, int>>> allRet;
vector<pair<int, int>> curRet;
DFS(allRet, curRet, 0, n);
return transResult(allRet, n);
}
};看完了這篇文章,相信你對“C++回溯算法深度優先搜索的示例分析”有了一定的了解,如果想了解更多相關知識,歡迎關注億速云行業資訊頻道,感謝各位的閱讀!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。