您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容介紹了“怎么用Python/R語言分別解決金字塔數求和問題”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!
階乘是基斯頓·卡曼(Christian Kramp,1760~1826)于 1808 年發明的運算符號,是數學術語。
n!=1∗2∗3∗...∗(n−1)∗n
或者可以使用遞歸方式定義:
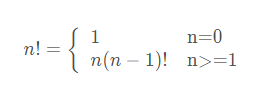
對其前N項階乘求和即是sum(1!+2!+3!+...+n!),有了以上的理論基礎,我們一起看看圖解,加強一下理解 !

如圖,如果要輸出每一個值 ,可以嵌入循環的思想,每一次將前一個值進行乘法運算即可!
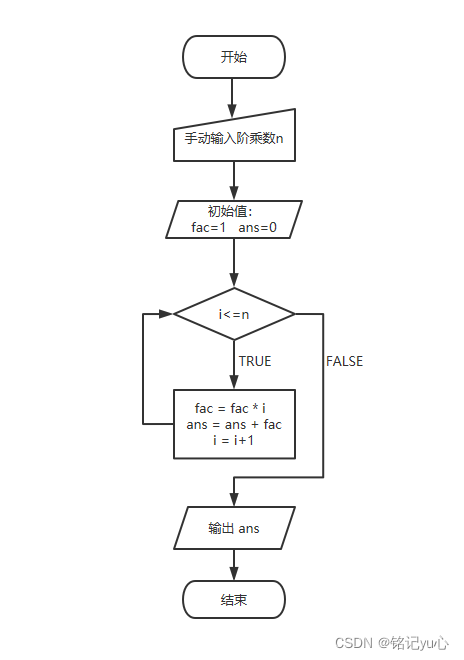
在此可以看到 ,我們需要加以人工控制需要算前多少項。在循環體內,這是對階乘數的累加和賦值。
1.3.1 python代碼實現
n = int(input("n = "))
s = 0
t = 1
for i in range(1,n+1):
t*=i
s+=t
print ("前{}階乘的和是:{}" .format(n,s))
1.3.2 R語言代碼實現
factorial <- function(n){
n <<- as.integer(readline("請輸入需要階乘個數(從 1 開始):"))
fac = 1
ans = 0
for (i in 1:n) {
fac = fac * i
ans = ans + fac
}
return(ans)
}
test_3 <- function(){
print("前n階乘之和為:")
factorial(n)
}
test_3()
這個實驗核心的點是循環的使用;
至于R代碼部分均使用函數的形式進行包裝方便理解;函數內部采用互動的方式,便于拓展使用。有需要了解的留言或私信。
此處的金字塔是真金字塔;就按簡單的金字塔形狀的數字:

求s=a+aa+aa+aaa+aa...a的值,其中 a 是一個數字。例如:
2+22+222+2222+22222
(此時共 有 5 個數相加),幾個數相加由鍵盤控制。
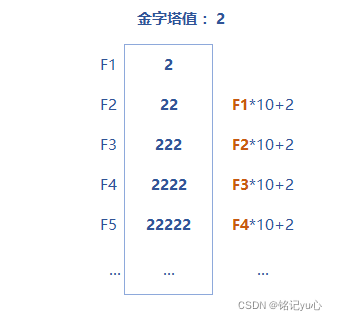
通過對每一層金字塔數的拆解,即可得到如下的通項公式:
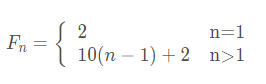
這樣問題不久又解決了嗎?與上面的前n項階乘求和一樣,使用循環求出每一層數,然后求和。
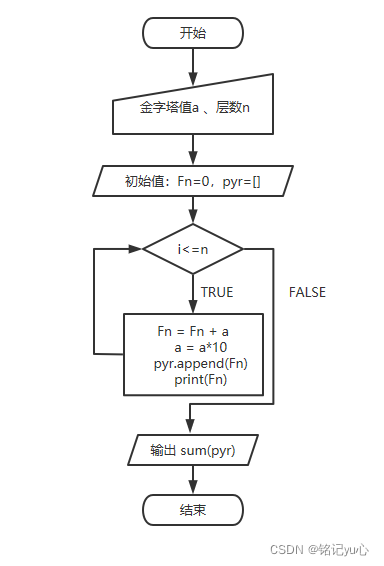
與上面實驗基本沒有差異;主要是循環體的算法不同而已。此處不做講解了。
2.3.1 python代碼
a = int(input("請輸入需要a的值:"))
n = int(input("請輸入需要n的值:"))
Fn = 0
pyr = []
for i in range(n):
Fn = Fn + a
a = a*10
pyr.append(Fn)
print(Fn)
print("前{}個數的和為:{}".format(n, sum(pyr)))
2.3.2 R語言代碼實現
sum_pyr <- function(){
a <- as.integer(readline("請輸入a的值:"))
n <- as.integer(readline("請輸入n的值:"))
Fn <- 0
pyr <- c()
for (i in 1:n) {
Fn <- Fn + a
a <- a * 10
pyr[i] <- Fn
print(Fn)
}
ans <<- sum(pyr)
}
test_4 <- function(){
print("金字塔為:")
sum_pyr()
print("求和結果為:")
ans
}
test_4()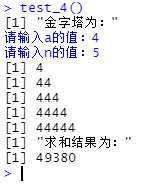
“怎么用Python/R語言分別解決金字塔數求和問題”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站,小編將為大家輸出更多高質量的實用文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。