您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
小編給大家分享一下JavaScript怎么實現四種常用排序,希望大家閱讀完這篇文章之后都有所收獲,下面讓我們一起去探討吧!
插入排序有直接插入排序,折半插入排序,希爾排序,這里只實現常用的直接插入排序
將左側序列看成一個有序序列,每次將一個數字插入該有序序列。
插入時,從有序序列最右側開始比較,若比較的數較大,后移一位。
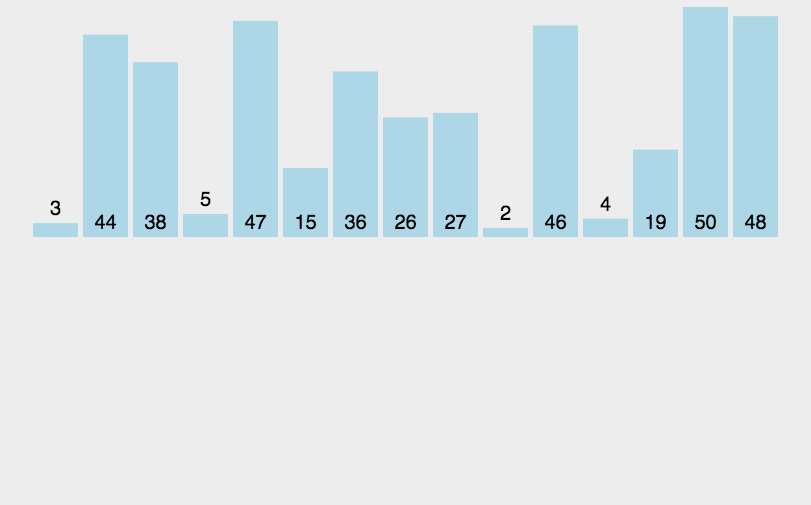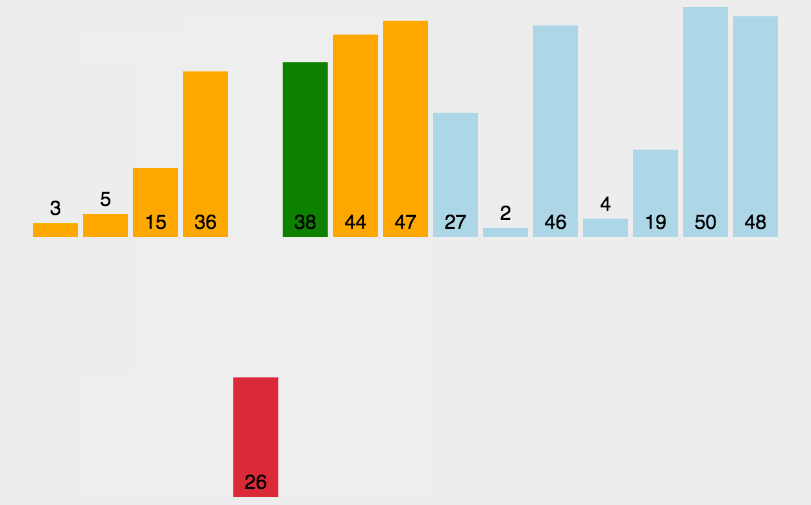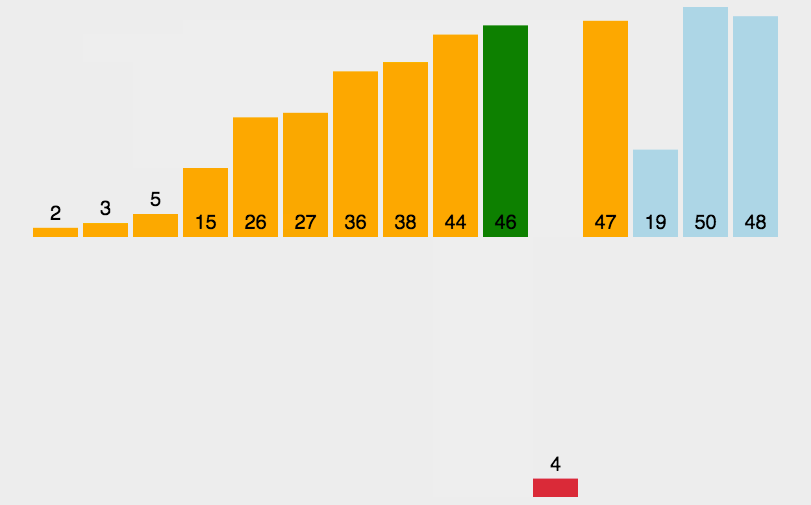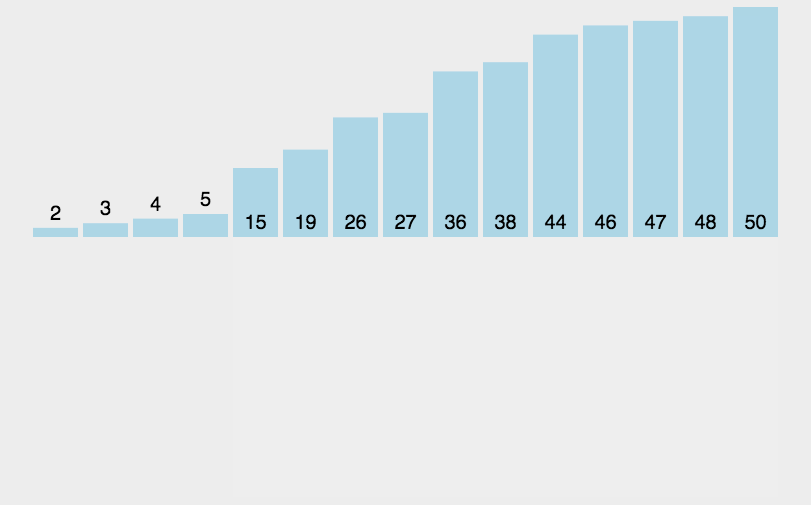
function insertSort(array) {
//第一個默認已經排好
for (let i = 1; i < array.length; i++) {
let target = i;
for (let j = i - 1; j >= 0; j--) {
if (array[target] < array[j]) {
[array[target], array[j]] = [array[j], array[target]]
target = j;
} else {
break;
}
}
}
return array;
}復雜度
時間復雜度:O(n2)
空間復雜度:O(1)
穩定性
穩定
循環數組,比較當前元素和上一個元素,如果當前元素比上一個元素小,向下冒泡。
這樣一次循環之后最前一個數就是本數組最小的數。
下一次循環繼續上面的操作,不循環已經排序好的數。
優化:當一次循環沒有發生冒泡,說明已經排序完成,停止循環。
function bubbleSort(array) {
//第一個循環是所需次數
for (let j = 0; j < array.length; j++) {
let complete = true;
for (let i = array.length-1; i>j; i--) {
// 比較相鄰數
if (array[i] < array[i -1]) {
[array[i], array[i - 1]] = [array[i - 1], array[i]];
complete = false;
}
}
// 沒有冒泡結束循環
if (complete) {
break;
}
}
return array;
}復雜度
時間復雜度:O(n2)
空間復雜度:O(1)
穩定性
穩定
快速排序:通過一趟排序將要排序的數據分割成獨立的兩部分,其中一部分的所有數據比另一部分的所有數據要小,再按這種方法對這兩部分數據分別進行快速排序,整個排序過程可以遞歸進行,使整個數據變成有序序列。
實現步驟:
選擇一個基準元素target(一般選擇第一個數)
將比target小的元素移動到數組左邊,比target大的元素移動到數組右邊
分別對target左側和右側的元素進行快速排序
從上面的步驟中我們可以看出,快速排序也利用了分治的思想(將問題分解成一些小問題遞歸求解)
下面是對序列6、1、2、7、9、3、4、5、10、8排序的過程:
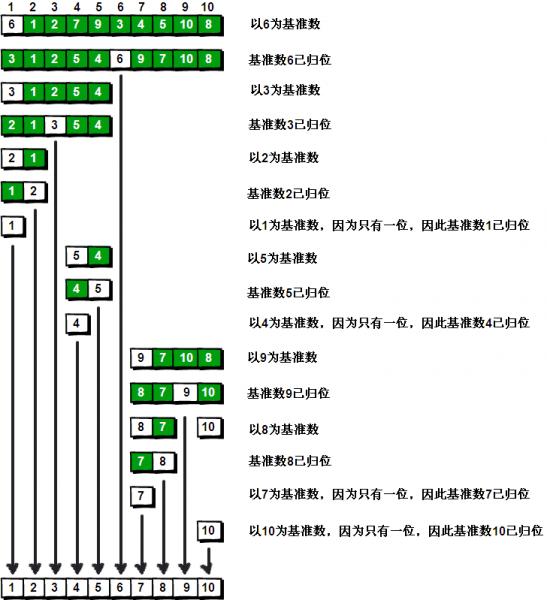
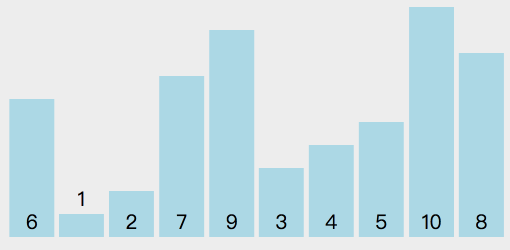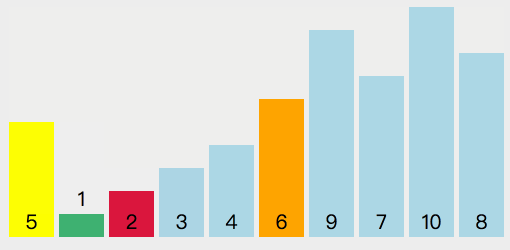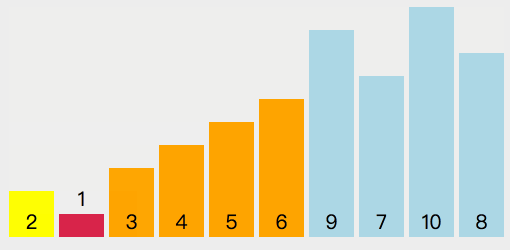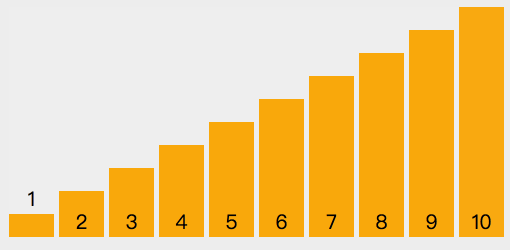
//JS自帶的sort()就是快排
function quickSort(array, start, end) {
if (end - start < 1) {
return;
}
const target = array[start];
let l = start;
let r = end;
while (l < r) {
while (l < r && array[r] >= target) {
r--;
}
array[l] = array[r];
while (l < r && array[l] < target) {
l++;
}
array[r] = array[l];
}
array[l] = target;
quickSort(array, start, l - 1);
quickSort(array, l + 1, end);
return array;
}復雜度
時間復雜度:平均O(nlogn),最壞O(n2),實際上大多數情況下小于O(nlogn)
空間復雜度:O(logn)(遞歸調用消耗)
穩定性
不穩定
每次循環選取一個最小的數字放到前面的有序序列中。
function selectionSort(array) {
for (let i = 0; i < array.length - 1; i++) {
let minIndex = i;
for (let j = i + 1; j < array.length; j++) {
if (array[j] < array[minIndex]) {
minIndex = j;
}
}
[array[minIndex], array[i]] = [array[i], array[minIndex]];
}
}復雜度
時間復雜度:O(n2)
空間復雜度:O(1)
穩定性
不穩定
創建一個大頂堆,大頂堆的堆頂一定是最大的元素。
交換第一個元素和最后一個元素,讓剩余的元素繼續調整為大頂堆。
從后往前以此和第一個元素交換并重新構建,排序完成。
function heapSort(array) {
creatHeap(array);
console.log(array);
// 交換第一個和最后一個元素,然后重新調整大頂堆
for (let i = array.length - 1; i > 0; i--) {
[array[i], array[0]] = [array[0], array[i]];
adjust(array, 0, i);
}
return array;
}
// 構建大頂堆,從第一個非葉子節點開始,進行下沉操作
function creatHeap(array) {
const len = array.length;
const start = parseInt(len / 2) - 1;
for (let i = start; i >= 0; i--) {
adjust(array, i, len);
}
}
// 將第target個元素進行下沉,孩子節點有比他大的就下沉
function adjust(array, target, len) {
for (let i = 2 * target + 1; i < len; i = 2 * i + 1) {
// 找到孩子節點中最大的
if (i + 1 < len && array[i + 1] > array[i]) {
i = i + 1;
}
// 下沉
if (array[i] > array[target]) {
[array[i], array[target]] = [array[target], array[i]]
target = i;
} else {
break;
}
}
}復雜度
時間復雜度:O(nlogn)
空間復雜度:O(1)
穩定性
不穩定
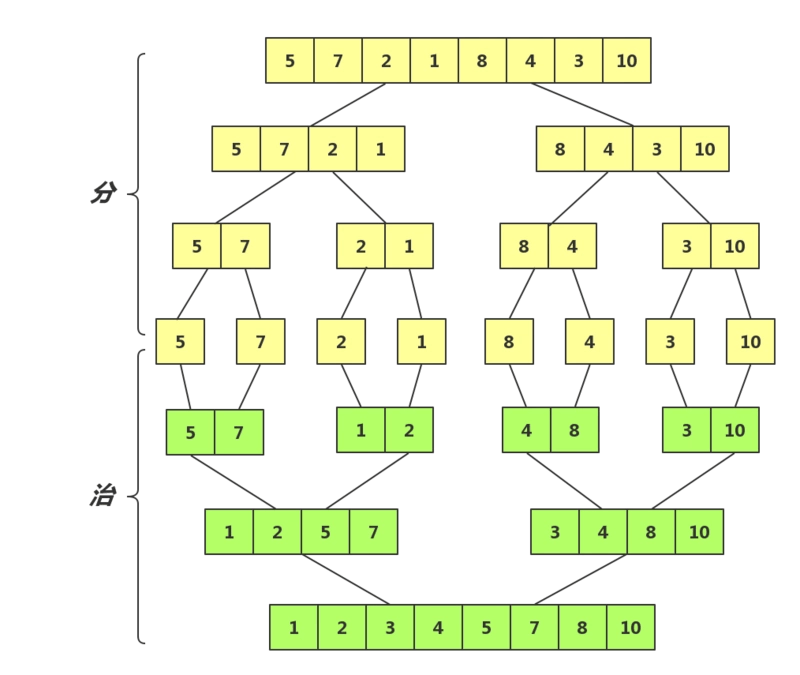
利用歸并的思想實現的排序方法。
該算法是采用分治法(Divide and Conquer)的一個非常典型的應用。(分治法將問題分成一些小的問題然后遞歸求解,而治的階段則將分的階段得到的各答案"修補"在一起,即分而治之)。
將已有序的子序列合并,得到完全有序的序列
即先使每個子序列有序,再使子序列段間有序
若將兩個有序表合并成一個有序表,稱為二路歸并
分割:
將數組從中點進行分割,分為左、右兩個數組
遞歸分割左、右數組,直到數組長度小于2
歸并:
如果需要合并,那么左右兩數組已經有序了。
創建一個臨時存儲數組temp,比較兩數組第一個元素,將較小的元素加入臨時數組
若左右數組有一個為空,那么此時另一個數組一定大于temp中的所有元素,直接將其所有元素加入temp
function mergeSort(array) {
if (array.length < 2) {
return array;
}
const mid = Math.floor(array.length / 2);
const front = array.slice(0, mid);
const end = array.slice(mid);
return merge(mergeSort(front), mergeSort(end));
}
function merge(front, end) {
const temp = [];
while (front.length && end.length) {
if (front[0] < end[0]) {
temp.push(front.shift());
} else {
temp.push(end.shift());
}
}
while (front.length) {
temp.push(front.shift());
}
while (end.length) {
temp.push(end.shift());
}
return temp;
}做題時,上面多了刪除過程,特別大的例子,時間也可能會超,用下面的方法
function merge(left, right){
let leftLen = left.length, rightLen = right.length;
let i = 0, j = 0;
let temp = new Array(leftLen + rightLen);
for(let cur = 0; cur < leftLen + rightLen; cur++){
// 檢查i, j有沒有超界
if(i >= leftLen) temp[cur]= right[j++];
else if(j >= rightLen) temp[cur] = left[i++];
else if(left[i] <= right[j]){
temp[cur] = left[i++];
}else{
temp[cur] = right[j++];
}
}
return temp;
}復雜度
時間復雜度:O(nlogn)
空間復雜度:O(n)
穩定性
穩定
看完了這篇文章,相信你對“JavaScript怎么實現四種常用排序”有了一定的了解,如果想了解更多相關知識,歡迎關注億速云行業資訊頻道,感謝各位的閱讀!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。