您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹了如何使用matlab遺傳算法求解車間調度問題,具有一定借鑒價值,感興趣的朋友可以參考下,希望大家閱讀完這篇文章之后大有收獲,下面讓小編帶著大家一起了解一下。
車間調度是指根據產品制造的合理需求分配加工車間順序,從而達到合理利用產品制造資源、提高企業經濟效益的目的。車間調度問題從數學上可以描述為有n個待加工的零件要在m臺機器上加工。問題需要滿足的條件包括每個零件的各道工序使用每臺機器不多于1次,每個零件都按照一定的順序進行加工。
傳統作業車間帶調度實例
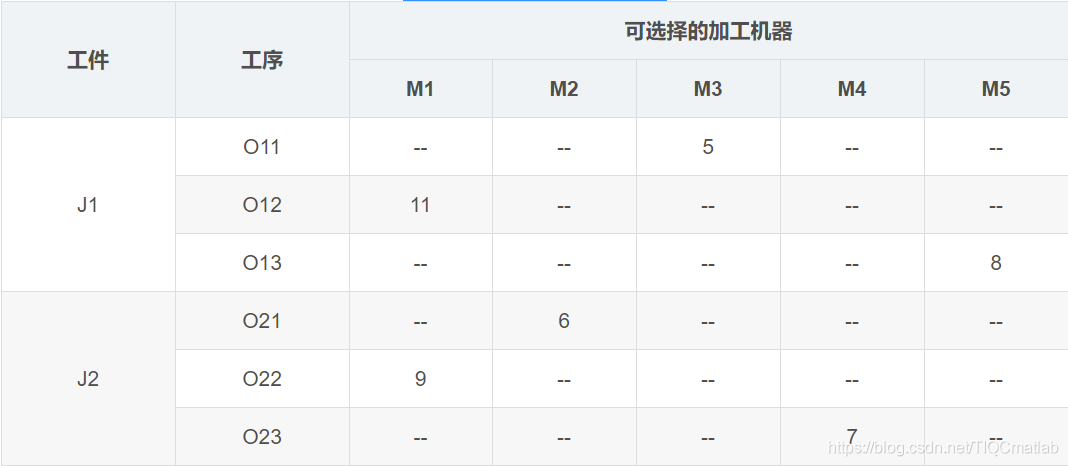
有若干工件,每個工件有若干工序,有多個加工機器,但是每道工序只能在一臺機器上加工。對應到上面表格中的實例就是,兩個工件,工件J1有三道工序,工序Q11只能在M3上加工,加工時間是5小時。
約束是對于一個工件來說,工序的相對順序不能變。O11->O12->O13。每時刻,每個工件只能在一臺機器上加工;每個機器上只能有一個工件。
調度的任務則是安排出工序的加工順序,加工順序確定了,因為每道工序只有一臺機器可用,加工的機器也就確定了。
調度的目的是總的完工時間最短(也可以是其他目標)。舉個例子,比如確定了O21->O22->O11->O23->O12->O13的加工順序之后,我們就可以根據加工機器的約束,計算出總的加工時間。
M2加工O21消耗6小時,工件J2當前加工時間6小時。
M1加工O22消耗9小時,工件J2當前加工時間6+9=15小時。
M3加工O11消耗5小時,工件J1當前加工時間5小時。
M4加工O23消耗7小時,工件J2加工時間15+7=22小時。
M1加工O12消耗11小時,但是要等M1加工完O22之后才開始加工O12,所以工件J1的當前加工時間為max(5,9)+11=20小時。
M5加工O13消耗8小時,工件J2加工時間20+8=28小時。
總的完工時間就是max(22,28)=28小時。
2 柔性作業車間調度
柔性作業車間帶調度實例(參考自高亮老師論文
《改進遺傳算法求解柔性作業車間調度問題》——機械工程學報)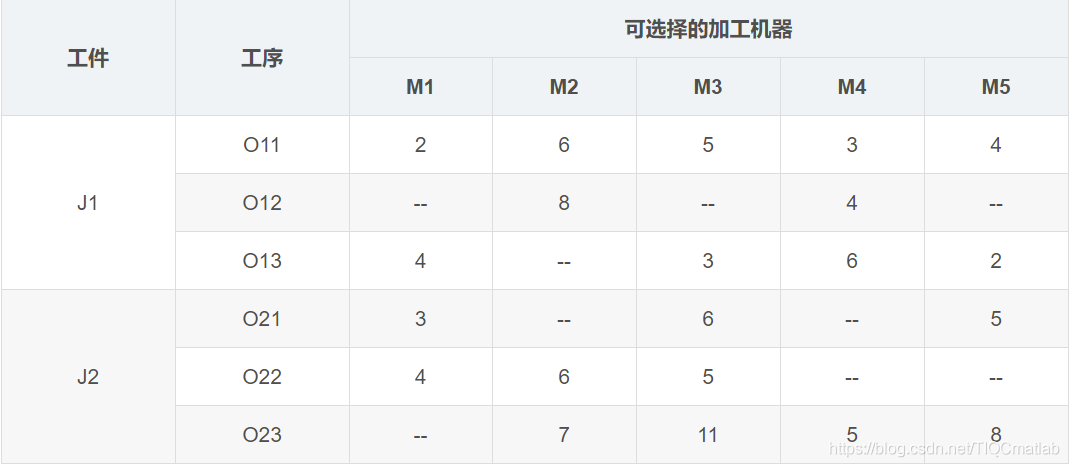
相比于傳統作業車間調度,柔性作業車間調度放寬了對加工機器的約束,更符合現實生產情況,每個工序可選加工機器變成了多個,可以由多個加工機器中的一個加工。比如上表中的實例,J1的O12工序可以選擇M2和M4加工,加工時間分別是8小時和4小時,但是并不一定選擇M4加工,最后得出來的總的完工時間就更短,所以,需要調度算法求解優化。
相比于傳統作業車間,柔性車間作業調度的調度任務不僅要確定工序的加工順序,而且需要確定每道工序的機器分配。比如,確定了O21->O22->O11->O23->O12->O13的加工順序,我們并不能相應工序的加工機器,所以還應該確定對應的[M1、M3、M5]->[M1、M2、M3]->[M1、M2、M3、M4、M5]->[M2、M3、M4、M5]->[M2、M4]->[M1、M3、M4、M5]的機器組合。調度的目的還是總的完工時間最短(也可以是其他目標,比如機器最大負荷最短、總的機器負荷最短)
遺傳算法(Genetic Algorithm,GA)是進化計算的一部分,是模擬達爾文的遺傳選擇和自然淘汰的生物進化過程的計算模型,是一種通過模擬自然進化過程搜索最優解的方法。該算法簡單、通用,魯棒性強,適于并行處理。
遺傳算法是一類可用于復雜系統優化的具有魯棒性的搜索算法,與傳統的優化算法相比,具有以下特點:
(1)以決策變量的編碼作為運算對象。傳統的優化算法往往直接利用決策變量的實際值本身來進行優化計算,但遺傳算法是使用決策變量的某種形式的編碼作為運算對象。這種對決策變量的編碼處理方式,使得我們在優化計算中可借鑒生物學中染色體和基因等概念,可以模仿自然界中生物的遺傳和進化激勵,也可以很方便地應用遺傳操作算子。
(2)直接以適應度作為搜索信息。傳統的優化算法不僅需要利用目標函數值,而且搜索過程往往受目標函數的連續性約束,有可能還需要滿足“目標函數的導數必須存在”的要求以確定搜索方向。遺傳算法僅使用由目標函數值變換來的適應度函數值就可確定進一步的搜索范圍,無需目標函數的導數值等其他輔助信息。直接利用目標函數值或個體適應度值也可以將搜索范圍集中到適應度較高部分的搜索空間中,從而提高搜索效率。
(3)使用多個點的搜索信息,具有隱含并行性。傳統的優化算法往往是從解空間的一個初始點開始最優解的迭代搜索過程。單個點所提供的搜索信息不多,所以搜索效率不高,還有可能陷入局部最優解而停滯;遺傳算法從由很多個體組成的初始種群開始最優解的搜索過程,而不是從單個個體開始搜索。對初始群體進行的、選擇、交叉、變異等運算,產生出新一代群體,其中包括了許多群體信息。這些信息可以避免搜索一些不必要的點,從而避免陷入局部最優,逐步逼近全局最優解。
(4) 使用概率搜索而非確定性規則。傳統的優化算法往往使用確定性的搜索方法,一個搜索點到另一個搜索點的轉移有確定的轉移方向和轉移關系,這種確定性可能使得搜索達不到最優店,限制了算法的應用范圍。遺傳算法是一種自適應搜索技術,其選擇、交叉、變異等運算都是以一種概率方式進行的,增加了搜索過程的靈活性,而且能以較大概率收斂于最優解,具有較好的全局優化求解能力。但,交叉概率、變異概率等參數也會影響算法的搜索結果和搜索效率,所以如何選擇遺傳算法的參數在其應用中是一個比較重要的問題。
綜上,由于遺傳算法的整體搜索策略和優化搜索方式在計算時不依賴于梯度信息或其他輔助知識,只需要求解影響搜索方向的目標函數和相應的適應度函數,所以遺傳算法提供了一種求解復雜系統問題的通用框架。它不依賴于問題的具體領域,對問題的種類有很強的魯棒性,所以廣泛應用于各種領域,包括:函數優化、組合優化生產調度問題、自動控制
、機器人學、圖像處理(圖像恢復、圖像邊緣特征提取…)、人工生命、遺傳編程、機器學習。
基本遺傳算法(Simple Genetic Algorithms,SGA)只使用選擇算子、交叉算子和變異算子這三種遺傳算子,進化過程簡單,是其他遺傳算法的基礎。
通過隨機方式產生若干由確定長度(長度與待求解問題的精度有關)編碼的初始群體;
通過適應度函數對每個個體進行評價,選擇適應度值高的個體參與遺傳操作,適應度低的個體被淘汰;
經遺傳操作(復制、交叉、變異)的個體集合形成新一代種群,直到滿足停止準則(進化代數GEN>=?);
將后代中變現最好的個體作為遺傳算法的執行結果。
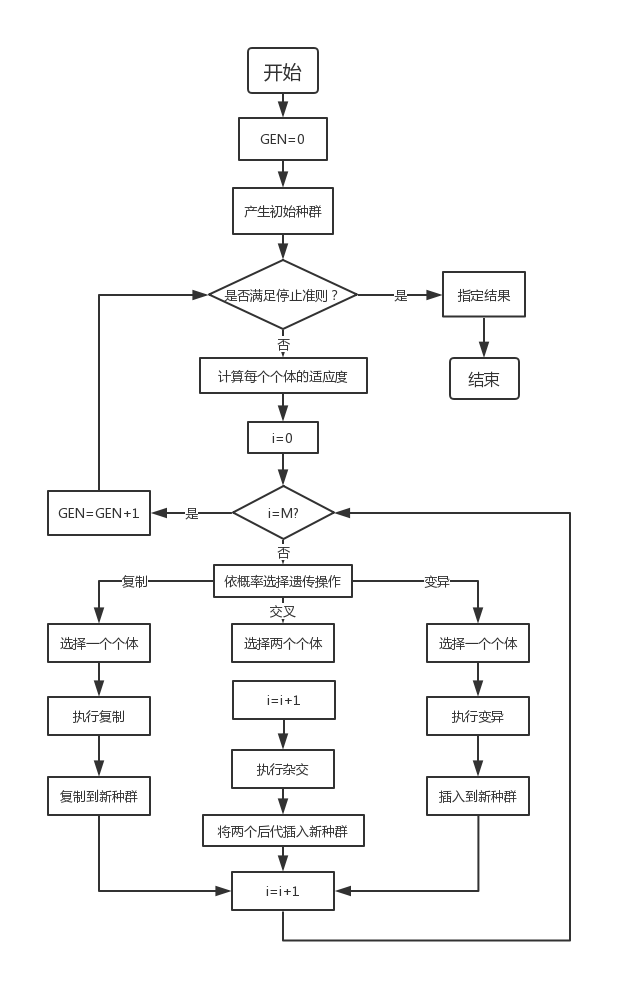
其中,GEN是當前代數;M是種群規模,i代表種群數量。
基本遺傳算法(SGA)由編碼、適應度函數、遺傳算子(選擇、交叉、變異)及運行參數組成。
(1)二進制編碼
二進制編碼的字符串長度與問題所求解的精度有關。需要保證所求解空間內的每一個個體都可以被編碼。
優點:編、解碼操作簡單,遺傳、交叉便于實現
缺點:長度大
(2)其他編碼方法
格雷碼、浮點數編碼、符號編碼、多參數編碼等
適應度函數要有效反映每一個染色體與問題的最優解染色體之間的差距。

交叉運算是指對兩個相互配對的染色體按某種方式相互交換其部分基因,從而形成兩個新的個體;交叉運算是遺傳算法區別于其他進化算法的重要特征,是產生新個體的主要方法。在交叉之前需要將群體中的個體進行配對,一般采取隨機配對原則。
常用的交叉方式:
單點交叉
雙點交叉(多點交叉,交叉點數越多,個體的結構被破壞的可能性越大,一般不采用多點交叉的方式)
均勻交叉
算術交叉
遺傳算法中的變異運算是指將個體染色體編碼串中的某些基因座上的基因值用該基因座的其他等位基因來替換,從而形成一個新的個體。
就遺傳算法運算過程中產生新個體的能力方面來說,交叉運算是產生新個體的主要方法,它決定了遺傳算法的全局搜索能力;而變異運算只是產生新個體的輔助方法,但也是必不可少的一個運算步驟,它決定了遺傳算法的局部搜索能力。交叉算子與變異算子的共同配合完成了其對搜索空間的全局搜索和局部搜索,從而使遺傳算法能以良好的搜索性能完成最優化問題的尋優過程。


具有低階、定義長度短,且適應度值高于群體平均適應度值的模式稱為基因塊或積木塊。
積木塊假設:個體的基因塊通過選擇、交叉、變異等遺傳算子的作用,能夠相互拼接在一起,形成適應度更高的個體編碼串。
積木塊假設說明了用遺傳算法求解各類問題的基本思想,即通過積木塊直接相互拼接在一起能夠產生更好的解。
clc;clear
%% 下載數據
% 加工數據包括加工時間,加工機器,機器數,各機器權重,工件數,各工件對應的工序數
load data operation_time operation_machine num_machine machine_weight num_job num_op
%% 基本參數
MAXGEN = 200; % 最大迭代次數
Ps = 0.8; % 選擇率
Pc = 0.7; % 交叉率
Pm = 0.3; % 變異率
sizepop = 200; % 個體數目
e = 0.5; % 目標值權重
trace = zeros(2,MAXGEN);
%% ===========================種群初始化============================
total_op_num=sum(num_op);
chroms=initialization(num_op,num_job,total_op_num,sizepop,operation_machine,operation_time);
[Z,~,~]=fitness(chroms,num_machine,e,num_job,num_op);
%% ============================迭代過程=============================
for gen=1:MAXGEN
fprintf('當前迭代次數:'),disp(gen)
% 輪盤賭選擇
chroms_new=selection(chroms,Z,Ps);
% 交叉操作
chroms_new=crossover(chroms_new,Pc,total_op_num,num_job,num_op);
% 變異操作
chroms_new=mutation(chroms_new,total_op_num,Pm,num_machine,e,num_job,num_op,operation_machine,operation_time);
% 計算選擇交叉變異后個體的適應度
[Z_new,~,~]=fitness(chroms_new,num_machine,e,num_job,num_op);
% 根據適應度在原種群和遺傳操作后的種群中選出sizepop個更優個體
[chroms,Z,chrom_best]=update_chroms(chroms,chroms_new,Z,Z_new,sizepop);
% 記錄每代的最優適應度與平均適應度
trace(1, gen)=Z(1);
trace(2, gen)=mean(Z);
% 更新全局最優適應度
if gen==1 || MinVal>trace(1,gen)
MinVal=trace(1,gen);
function [Z,machine_weight,pvals] = fitness(chroms,num_machine,e,num_job,num_op)
sizepop=size(chroms,1);
pvals=cell(1,sizepop);
Z1=zeros(1,sizepop);
Z2=Z1;
total_op_num=sum(num_op); % 總工序數
for k=1:sizepop
chrom=chroms(k,:);
machine=zeros(1,num_machine); % 記錄各機器變化時間
job=zeros(1,num_job); % 記錄各工件變化時間
machine_time=zeros(1,num_machine); % 計算各機器的實際加工時間
pval=zeros(2,total_op_num); % 記錄各工序開始和結束時間
for i=1:total_op_num
% 機器時間大于工件時間
if machine(chrom(total_op_num+i))>=job(chrom(i))
pval(1,i)=machine(chrom(total_op_num+i)); % 記錄工件開始時間
machine(chrom(total_op_num+i))=machine(chrom(total_op_num+i))+chrom(total_op_num*2+i);
job(chrom(i))=machine(chrom(total_op_num+i));
pval(2,i)=machine(chrom(total_op_num+i)); % 記錄工件結束時間
% 機器時間小于工件時間
else
pval(1,i)=job(chrom(i));
job(chrom(i))=job(chrom(i))+chrom(total_op_num*2+i);
machine(chrom(total_op_num+i))=job(chrom(i));
pval(2,i)=job(chrom(i));
end
machine_time(chrom(total_op_num+i))=machine_time(chrom(total_op_num+i))+chrom(total_op_num*2+i);
end
Z1(k)=max(machine); % 最大機器時間值,對應makespan
% machine_weight=machine_time/sum(machine_time); % 計算各機器的負荷
machine_weight=machine_time;
Z2(k)=max(machine_weight)-min(machine_weight);
pvals{k}=pval;
end
% min_makespan=min(Z1);%所有染色體的makespan最優值
% max_makespan=max(Z1);
% min_weight=min(Z2);%負載最優值
% max_weight=max(Z2);
% Z=e*((Z1-min_makespan)./(max_makespan-min_makespan))+(1-e)*((Z2-min_weight)./(max_weight-min_weight));%計算適應度
Z=e*Z1+(1-e)*Z2;
function [ chroms_new] = crossover(chroms,Pc,total_op_num,num_job,num_op)
size_chrom=size(chroms,1); % 染色體數
chroms_new=chroms;
%% 面向工序碼的交叉操作
for i=1:2:size_chrom-1
if Pc>rand
% 父代染色體
parent1=chroms(i,:);
parent2=chroms(i+1,:);
Job=randperm(num_job);
% 將工件隨機分成兩個集合
J1=Job(1:round(num_job/2));
J2=Job(length(J1)+1:end);
% 子代染色體
child1=parent1;
child2=parent2;
op_p1=[];
op_p2=[];
for j=1:length(J2)
%找出父代中J2片段對應的位置
op_p1=[op_p1,find(parent1(1:total_op_num)==J2(j))];
op_p2=[op_p2,find(parent2(1:total_op_num)==J2(j))];
end
op_s1=sort(op_p1);
op_s2=sort(op_p2);
% 子代1交換J2片段的基因,機器碼對應位置的基因,工時碼對應位置的基因
child1(op_s1)=parent2(op_s2);
child1(total_op_num+op_s1)=parent2(total_op_num+op_s2);
child1(total_op_num*2+op_s1)=parent2(total_op_num*2+op_s2);
% 子代2同理
child2(op_s2)=parent1(op_s1);
child2(total_op_num+op_s2)=parent1(total_op_num+op_s1);
child2(total_op_num*2+op_s2)=parent1(total_op_num*2+op_s1);
chroms_new(i,:)=child1;
chroms_new(i+1,:)=child2;
end
end
%% 面向機器碼的交叉操作
for k=1:2:size_chrom-1
if Pc>rand
parent1=chroms_new(k,:);
parent2=chroms_new(k+1,:);
child1=parent1;
child2=parent2;
% 隨機產生與染色體長度相等的0,1序列
rand0_1=randi([0,1],1,total_op_num);
for n=1:num_job
ind_0=find(rand0_1(num_op(n)*(n-1)+1:num_op(n)*n)==0);
if ~isempty(ind_0)
temp1=find(parent1(1:total_op_num)==n);
temp2=find(parent2(1:total_op_num)==n);
child1(total_op_num+temp1(ind_0))=parent2(total_op_num+temp2(ind_0));
child2(total_op_num+temp2(ind_0))=parent1(total_op_num+temp1(ind_0));
child1(total_op_num*2+temp1(ind_0))=parent2(total_op_num*2+temp2(ind_0));
child2(total_op_num*2+temp2(ind_0))=parent1(total_op_num*2+temp1(ind_0));
end
end
chroms_new(k,:)=child1;
chroms_new(k+1,:)=child2;
end
end
end
感謝你能夠認真閱讀完這篇文章,希望小編分享的“如何使用matlab遺傳算法求解車間調度問題”這篇文章對大家有幫助,同時也希望大家多多支持億速云,關注億速云行業資訊頻道,更多相關知識等著你來學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。