您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容主要講解“Java平衡二叉樹怎么實現”,感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷,實用性強。下面就讓小編來帶大家學習“Java平衡二叉樹怎么實現”吧!
簡單來說,就是方便搜索的二叉樹,是一種具備特定結構的二叉樹,即,對于節點n,其左子樹的所有節點的值都小于等于其值,其右子樹的所有節點的值都大于等于其值。
以序列2,4,1,3,5,10,9,8為例,如果以二叉搜索樹建樹的方式,我們建立出來的逐個步驟應該為
第一步:

第二步:
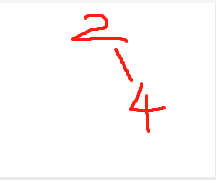
第三步:
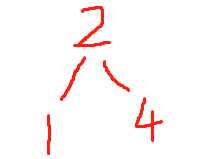
第四步:
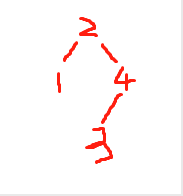
第五步:
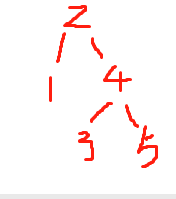
第六步:
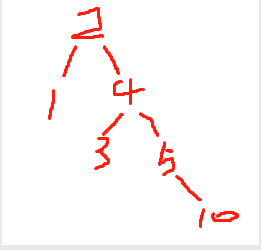
第七步:
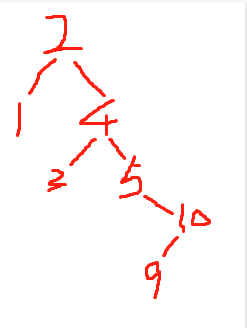
第八步:
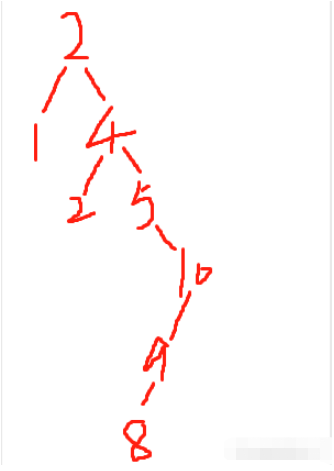
按照不平衡的普通方法生成的二叉搜索樹就是這么一個樣子。其實現代碼如下:
package com.chaojilaji.book.searchtree;
import com.chaojilaji.auto.autocode.utils.Json;
import java.util.Objects;
public class SearchTreeUtils {
public static SearchTree buildTree(SearchTree searchTree, Integer value) {
if (value >= searchTree.getValue()) {
if (Objects.isNull(searchTree.getRightChild())) {
SearchTree searchTree1 = new SearchTree();
searchTree1.setValue(value);
searchTree.setRightChild(searchTree1);
} else {
buildTree(searchTree.getRightChild(), value);
}
} else {
if (Objects.isNull(searchTree.getLeftChild())) {
SearchTree searchTree1 = new SearchTree();
searchTree1.setValue(value);
searchTree.setLeftChild(searchTree1);
} else {
buildTree(searchTree.getLeftChild(), value);
}
}
return searchTree;
}
public static void main(String[] args) {
int[] a = new int[]{2, 4, 1, 3, 5, 10, 9, 8};
SearchTree searchTree = new SearchTree();
searchTree.setValue(a[0]);
for (int i = 1; i < a.length; i++) {
searchTree = buildTree(searchTree,a[i]);
}
System.out.println(Json.toJson(searchTree));
}
}運行的結果如下:
{
"value": 2,
"left_child": {
"value": 1,
"left_child": null,
"right_child": null
},
"right_child": {
"value": 4,
"left_child": {
"value": 3,
"left_child": null,
"right_child": null
},
"right_child": {
"value": 5,
"left_child": null,
"right_child": {
"value": 10,
"left_child": {
"value": 9,
"left_child": {
"value": 8,
"left_child": null,
"right_child": null
},
"right_child": null
},
"right_child": null
}
}
}
}與我們的目標結果是一致的。
好了,那我們本節就完畢了。可是轉過頭可能你也發現了,直接生成的這個二叉搜索樹似乎有點太長了,層數有點太多了,一般來說,一個長度為8的序列,四層結構的二叉樹就可以表現出來了,這里卻使用了六層,顯然這樣的結果不盡人意,同時太深的層數,也增加了查找的時間復雜度。
這就給我們的樹提了要求,我們需要將目前構造出來的樹平衡一下,讓這棵二叉搜索樹的左右子樹“重量”最好差不多。
首先需要掌握兩個概念
平衡因子
旋轉
平衡因子就是對于這棵二叉搜索樹的每個節點來說,其左子樹的高度減去右子樹的高度即為該節點的平衡因子,該數值能很快的辨別出該節點究竟是左子樹高還是右子樹高。在平衡二叉樹中規定,當一個節點的平衡因子的絕對值大于等于2的時候,我們就認為該節點不平衡,需要進行調整。那么這種調整的手段稱之為節點與節點的旋轉,通俗來說,旋轉就是指的節點間的指向關系發生變化,在c語言中就是指針指向的切換。
在調用旋轉之前,我們需要判斷整棵樹是否平衡,即,這棵二叉搜索樹的所有平衡因子是否有絕對值大于等于2的,如果有,就找出最小的一棵子樹。可以確定的是,如果前一次二叉搜索樹是平衡的,那么此時如果加一個節點進去,造成不平衡,那么節點從葉子開始回溯,找到的第一個大于等于2的節點勢必為最小不平衡子樹的根節點。
對于這棵最小不平衡的子樹,我們需要得到兩個值,即根節點的平衡因子a,以及左右子樹根節點中平衡因子絕對值較大者的平衡因子b。
我們可以將需要旋轉的類型抽象為以下四種:
1.左左型(正正型,即 a>0 && b>0)
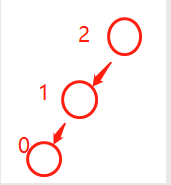
左左型最后想要達到的目標是第二個節點成為根節點,第一個節點成為第二個節點的右節點。
所以用偽代碼展示就是(設a1,a2,a3分別為圖里面從上到下的三個節點)
a2的右子樹 = (合并(a2的右子樹,a1的右子樹) + a1頂點值) 一起構成的二叉搜索樹;
返回 a2
2.左右型(正負型,即 a>0 && b<0)
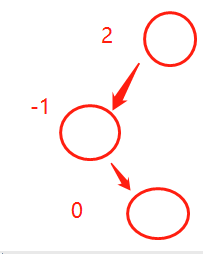
設a1,a2,a3分別為圖里面從上到下的三個節點
首先應該通過將a3和a2調換上下位置,使之變成左左型,然后再調用左左型的方法就完成了。
從左右型調換成左左型,即將a2及其左子樹成為a3左子樹的一部分,然后將a1的左子樹置為a3即可。
偽代碼如下:
a3的左子樹 = a2及其左子樹與a3的左子樹合并成的一棵二叉搜索樹;
a1的左子樹 = a3;
3.右右型(負負型,即 a<0 && b<0)
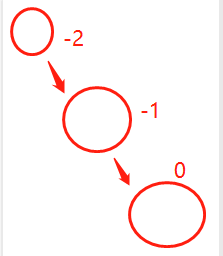
設a1,a2,a3分別為圖里面從上到下的三個節點
右右型與左左型類似,要達到的目的就是a1成為a2左子樹的一部分,偽代碼為:
a2的左子樹 = (合并a2的左子樹和a1的左子樹)+ a1頂點的值構成的二叉搜索樹;
返回a2
4.右左型(負正型,即 a<0 && b>0)
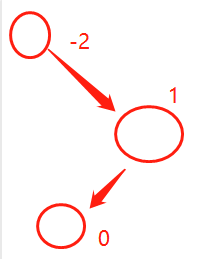
設a1,a2,a3分別為圖里面從上到下的三個節點
右左型需要先轉換成右右型,然后在調用右右型的方法即可。
從右左型到右右型,即需要將a2及其右子樹成為a3右子樹的一部分,然后將a1的右子樹置為a3即可。
偽代碼如下:
a3的右子樹 = a2及其右子樹與a3的右子樹合并成的一棵二叉搜索樹;
a1的右子樹 = a3;
從上面的分析可以得出,我們不僅僅需要實現旋轉的方法,還需要實現合并二叉樹等方法,這些方法都是基礎方法,讀者需要確保會快速寫出來。
請讀者朋友們根據上面的內容,先嘗試寫出集中平衡化的方法。
平衡二叉搜索樹建樹,需要在二叉搜索樹建樹的基礎上加上平衡的過程,即子樹之間指針轉換的問題,同時,由于這種指針轉換引起的子樹的子樹也會產生不平衡,所以上面提到的四種旋轉調整方式都是遞歸的。
首先,先構建節點基礎結構:
public class SearchTree {
private Integer value;
private SearchTree leftChild;
private SearchTree rightChild;
private Integer balanceNumber = 0;
private Integer height = 0;
}值,高度,平衡因子,左子樹,右子樹
這是計算二叉搜索樹中每個平衡因子的基礎,我們設最低層為高度1,則計算節點高度的代碼為:
public static Integer countHeight(SearchTree searchTree) {
if (Objects.isNull(searchTree)) {
return 0;
}
searchTree.setHeight(Math.max(countHeight(searchTree.getLeftChild()),
countHeight(searchTree.getRightChild())) + 1);
return searchTree.getHeight();
}這里有個半動態規劃的結論:當前節點的高度,等于左右子樹的最大高度+1;這里的寫法有點樹形DP的味道。
public static void countBalanceNumber(SearchTree searchTree, MaxNumber max, SearchTree fatherTree, Integer type) {
if (Objects.nonNull(searchTree.getValue())) {
if (Objects.isNull(searchTree.getLeftChild())
&& Objects.nonNull(searchTree.getRightChild())) {
searchTree.setBalanceNumber(-searchTree.getRightChild().getHeight());
}
if (Objects.nonNull(searchTree.getLeftChild())
&& Objects.isNull(searchTree.getRightChild())) {
searchTree.setBalanceNumber(searchTree.getLeftChild().getHeight());
}
if (Objects.isNull(searchTree.getLeftChild())
&& Objects.isNull(searchTree.getRightChild())) {
searchTree.setBalanceNumber(0);
}
if (Objects.nonNull(searchTree.getLeftChild())
&& Objects.nonNull(searchTree.getRightChild())) {
searchTree.setBalanceNumber(searchTree.getLeftChild().getHeight()
- searchTree.getRightChild().getHeight());
}
}
if (Objects.nonNull(searchTree.getLeftChild())) {
countBalanceNumber(searchTree.getLeftChild(), max, searchTree, 1);
}
if (Objects.nonNull(searchTree.getRightChild())) {
countBalanceNumber(searchTree.getRightChild(), max, searchTree, 2);
}
}本質上講,平衡因子就是左子樹高度減去右子樹高度,注意這里左右子樹都有可能不存在,所以加入了一堆特判。
判斷當前二叉樹是否平衡
static class MaxNumber {
public Integer max;
public SearchTree childTree;
public SearchTree fatherTree;
public Integer flag = 0; // 0 代表自己就是根,1代表childTree是左子樹,2代表childTree是右子樹
}
public static MaxNumber checkBalance(SearchTree searchTree) {
MaxNumber max = new MaxNumber();
max.max = 0;
countBalanceNumber(searchTree, max, null, 0);
return max;
}
public static void countBalanceNumber(SearchTree searchTree, MaxNumber max, SearchTree fatherTree, Integer type) {
if (Objects.nonNull(searchTree.getValue())) {
if (Objects.isNull(searchTree.getLeftChild())
&& Objects.nonNull(searchTree.getRightChild())) {
searchTree.setBalanceNumber(-searchTree.getRightChild().getHeight());
}
if (Objects.nonNull(searchTree.getLeftChild())
&& Objects.isNull(searchTree.getRightChild())) {
searchTree.setBalanceNumber(searchTree.getLeftChild().getHeight());
}
if (Objects.isNull(searchTree.getLeftChild())
&& Objects.isNull(searchTree.getRightChild())) {
searchTree.setBalanceNumber(0);
}
if (Objects.nonNull(searchTree.getLeftChild())
&& Objects.nonNull(searchTree.getRightChild())) {
searchTree.setBalanceNumber(searchTree.getLeftChild().getHeight()
- searchTree.getRightChild().getHeight());
}
}
if (Objects.nonNull(searchTree.getLeftChild())) {
countBalanceNumber(searchTree.getLeftChild(), max, searchTree, 1);
}
if (Objects.nonNull(searchTree.getRightChild())) {
countBalanceNumber(searchTree.getRightChild(), max, searchTree, 2);
}
if (Math.abs(searchTree.getBalanceNumber()) >= Math.abs(max.max)) {
if (Math.abs(searchTree.getBalanceNumber()) == Math.abs(max.max)
&& max.childTree == null) {
max.childTree = searchTree;
max.fatherTree = fatherTree;
max.flag = type;
max.max = searchTree.getBalanceNumber();
}
if (Math.abs(searchTree.getBalanceNumber()) > Math.abs(max.max)) {
max.childTree = searchTree;
max.fatherTree = fatherTree;
max.flag = type;
max.max = searchTree.getBalanceNumber();
}
}
}其中,MaxNumber類是為了保存第一棵不平衡的子樹而存在的結構,為了使這棵子樹平衡之后能重新回到整棵樹中,需要在MaxNumber中存儲當前子樹父節點,同時標明當前子樹是父節點的左子樹還是右子樹,還是本身。
public static void getAllValue(SearchTree tree, Set<Integer> sets) {
if (Objects.isNull(tree)) return;
if (Objects.nonNull(tree.getValue())) {
sets.add(tree.getValue());
}
if (Objects.nonNull(tree.getLeftChild())) {
getAllValue(tree.getLeftChild(), sets);
}
if (Objects.nonNull(tree.getRightChild())) {
getAllValue(tree.getRightChild(), sets);
}
}
/**
* 合并兩棵二叉搜索樹
*
* @param a
* @param b
* @return
*/
public static SearchTree mergeTree(SearchTree a, SearchTree b) {
Set<Integer> vals = new HashSet<>();
getAllValue(b, vals);
for (Integer c : vals) {
a = buildTree(a, c);
}
return a;
}將一棵樹轉成數字集合,然后通過建樹的方式建到另外一棵樹上即可。
1.左左型旋轉
/**
* 左左
*
* @param searchTree
* @return
*/
public static SearchTree leftRotate1(SearchTree father, SearchTree searchTree) {
SearchTree b = father;
SearchTree newRight = mergeTree(father.getRightChild(), searchTree.getRightChild());
newRight = buildTree(newRight, b.getValue());
countHeight(newRight);
while (Math.abs(checkBalance(newRight).childTree.getBalanceNumber()) >= 2) {
newRight = rotate(checkBalance(newRight).childTree);
countHeight(newRight);
}
searchTree.setRightChild(newRight);
return searchTree;
}2.右右型旋轉
/**
* 右右
* @param father
* @param searchTree
* @return
*/
public static SearchTree rightRotate1(SearchTree father, SearchTree searchTree) {
SearchTree b = father;
SearchTree newLeft = mergeTree(father.getLeftChild(), searchTree.getLeftChild());
newLeft = buildTree(newLeft, b.getValue());
countHeight(newLeft);
while (Math.abs(checkBalance(newLeft).childTree.getBalanceNumber()) >= 2) {
newLeft = rotate(checkBalance(newLeft).childTree);
countHeight(newLeft);
}
searchTree.setLeftChild(newLeft);
return searchTree;
}3.左右型旋轉
/**
* 左右
*
* @param searchTree
* @return
*/
public static SearchTree rightRotate2(SearchTree father, SearchTree searchTree) {
SearchTree a1 = father;
SearchTree a2 = searchTree;
SearchTree a3 = searchTree.getRightChild();
SearchTree newLeft = mergeTree(a2.getLeftChild(), a3.getLeftChild());
newLeft = buildTree(newLeft, a2.getValue());
countHeight(newLeft);
while (Math.abs(checkBalance(newLeft).childTree.getBalanceNumber()) >= 2) {
newLeft = rotate(checkBalance(newLeft).childTree);
countHeight(newLeft);
}
a3.setLeftChild(newLeft);
a1.setLeftChild(a3);
return a1;
}4.右左型旋轉
/**
* 右左
*
* @param searchTree
* @return
*/
public static SearchTree leftRotate2(SearchTree father, SearchTree searchTree) {
SearchTree a1 = father;
SearchTree a2 = searchTree;
SearchTree a3 = searchTree.getLeftChild();
SearchTree newRight = mergeTree(a2.getRightChild(), a3.getRightChild());
newRight = buildTree(newRight, a2.getValue());
countHeight(newRight);
while (Math.abs(checkBalance(newRight).childTree.getBalanceNumber()) >= 2) {
newRight = rotate(checkBalance(newRight).childTree);
countHeight(newRight);
}
a3.setRightChild(newRight);
a1.setRightChild(a3);
return a1;
}旋轉調用函數:
public static SearchTree rotate(SearchTree searchTree) {
int a = searchTree.getBalanceNumber();
if (Math.abs(a) < 2) {
return searchTree;
}
int b = Objects.isNull(searchTree.getLeftChild()) ? 0
: searchTree.getLeftChild().getBalanceNumber();
int c = Objects.isNull(searchTree.getRightChild()) ? 0
: searchTree.getRightChild().getBalanceNumber();
if (a > 0) {
if (b > 0) {
// TODO: 2022/1/13 左左
searchTree = leftRotate1(searchTree, searchTree.getLeftChild());
} else {
// TODO: 2022/1/13 左右
searchTree = rightRotate2(searchTree, searchTree.getLeftChild());
searchTree = leftRotate1(searchTree, searchTree.getLeftChild());
}
} else {
if (c > 0) {
// TODO: 2022/1/13 右左
searchTree = leftRotate2(searchTree, searchTree.getRightChild());
searchTree = rightRotate1(searchTree, searchTree.getRightChild());
} else {
// TODO: 2022/1/13 右右
searchTree = rightRotate1(searchTree, searchTree.getRightChild());
}
}
return searchTree;
}package com.chaojilaji.book.searchtree;
import com.chaojilaji.auto.autocode.utils.Json;
import com.chaojilaji.book.tree.Handle;
import com.chaojilaji.book.tree.Tree;
import org.omg.CORBA.OBJ_ADAPTER;
import java.util.HashSet;
import java.util.Objects;
import java.util.Set;
public class SearchTreeUtils {
static class MaxNumber {
public Integer max;
public SearchTree childTree;
public SearchTree fatherTree;
public Integer flag = 0; // 0 代表自己就是根,1代表childTree是左子樹,2代表childTree是右子樹
}
public static SearchTree rotate(SearchTree searchTree) {
int a = searchTree.getBalanceNumber();
if (Math.abs(a) < 2) {
return searchTree;
}
int b = Objects.isNull(searchTree.getLeftChild()) ? 0 : searchTree.getLeftChild().getBalanceNumber();
int c = Objects.isNull(searchTree.getRightChild()) ? 0 : searchTree.getRightChild().getBalanceNumber();
if (a > 0) {
if (b > 0) {
// TODO: 2022/1/13 左左
searchTree = leftRotate1(searchTree, searchTree.getLeftChild());
} else {
// TODO: 2022/1/13 左右
searchTree = rightRotate2(searchTree, searchTree.getLeftChild());
searchTree = leftRotate1(searchTree, searchTree.getLeftChild());
}
} else {
if (c > 0) {
// TODO: 2022/1/13 右左
searchTree = leftRotate2(searchTree, searchTree.getRightChild());
searchTree = rightRotate1(searchTree, searchTree.getRightChild());
} else {
// TODO: 2022/1/13 右右
searchTree = rightRotate1(searchTree, searchTree.getRightChild());
}
}
return searchTree;
}
public static void getAllValue(SearchTree tree, Set<Integer> sets) {
if (Objects.isNull(tree)) return;
if (Objects.nonNull(tree.getValue())) {
sets.add(tree.getValue());
}
if (Objects.nonNull(tree.getLeftChild())) {
getAllValue(tree.getLeftChild(), sets);
}
if (Objects.nonNull(tree.getRightChild())) {
getAllValue(tree.getRightChild(), sets);
}
}
/**
* 合并兩棵二叉搜索樹
*
* @param a
* @param b
* @return
*/
public static SearchTree mergeTree(SearchTree a, SearchTree b) {
Set<Integer> vals = new HashSet<>();
getAllValue(b, vals);
for (Integer c : vals) {
a = buildTree(a, c);
}
return a;
}
/**
* 左左
*
* @param searchTree
* @return
*/
public static SearchTree leftRotate1(SearchTree father, SearchTree searchTree) {
SearchTree b = father;
SearchTree newRight = mergeTree(father.getRightChild(), searchTree.getRightChild());
newRight = buildTree(newRight, b.getValue());
countHeight(newRight);
while (Math.abs(checkBalance(newRight).childTree.getBalanceNumber()) >= 2) {
newRight = rotate(checkBalance(newRight).childTree);
countHeight(newRight);
}
searchTree.setRightChild(newRight);
return searchTree;
}
/**
* 右左
*
* @param searchTree
* @return
*/
public static SearchTree leftRotate2(SearchTree father, SearchTree searchTree) {
SearchTree a1 = father;
SearchTree a2 = searchTree;
SearchTree a3 = searchTree.getLeftChild();
SearchTree newRight = mergeTree(a2.getRightChild(), a3.getRightChild());
newRight = buildTree(newRight, a2.getValue());
countHeight(newRight);
while (Math.abs(checkBalance(newRight).childTree.getBalanceNumber()) >= 2) {
newRight = rotate(checkBalance(newRight).childTree);
countHeight(newRight);
// System.out.println(Json.toJson(newRight));
}
a3.setRightChild(newRight);
a1.setRightChild(a3);
return a1;
}
/**
* 右右
* @param father
* @param searchTree
* @return
*/
public static SearchTree rightRotate1(SearchTree father, SearchTree searchTree) {
SearchTree b = father;
SearchTree newLeft = mergeTree(father.getLeftChild(), searchTree.getLeftChild());
newLeft = buildTree(newLeft, b.getValue());
countHeight(newLeft);
// TODO: 2022/1/13 合并后的也有可能有問題
while (Math.abs(checkBalance(newLeft).childTree.getBalanceNumber()) >= 2) {
newLeft = rotate(checkBalance(newLeft).childTree);
countHeight(newLeft);
// System.out.println(Json.toJson(newLeft));
}
searchTree.setLeftChild(newLeft);
return searchTree;
}
/**
* 左右
*
* @param searchTree
* @return
*/
public static SearchTree rightRotate2(SearchTree father, SearchTree searchTree) {
SearchTree a1 = father;
SearchTree a2 = searchTree;
SearchTree a3 = searchTree.getRightChild();
SearchTree newLeft = mergeTree(a2.getLeftChild(), a3.getLeftChild());
newLeft = buildTree(newLeft, a2.getValue());
countHeight(newLeft);
while (Math.abs(checkBalance(newLeft).childTree.getBalanceNumber()) >= 2) {
newLeft = rotate(checkBalance(newLeft).childTree);
countHeight(newLeft);
}
a3.setLeftChild(newLeft);
a1.setLeftChild(a3);
return a1;
}
public static MaxNumber checkBalance(SearchTree searchTree) {
MaxNumber max = new MaxNumber();
max.max = 0;
countBalanceNumber(searchTree, max, null, 0);
return max;
}
public static Integer countHeight(SearchTree searchTree) {
if (Objects.isNull(searchTree)) {
return 0;
}
searchTree.setHeight(Math.max(countHeight(searchTree.getLeftChild()), countHeight(searchTree.getRightChild())) + 1);
return searchTree.getHeight();
}
public static void countBalanceNumber(SearchTree searchTree, MaxNumber max, SearchTree fatherTree, Integer type) {
if (Objects.nonNull(searchTree.getValue())) {
if (Objects.isNull(searchTree.getLeftChild()) && Objects.nonNull(searchTree.getRightChild())) {
searchTree.setBalanceNumber(-searchTree.getRightChild().getHeight());
}
if (Objects.nonNull(searchTree.getLeftChild()) && Objects.isNull(searchTree.getRightChild())) {
searchTree.setBalanceNumber(searchTree.getLeftChild().getHeight());
}
if (Objects.isNull(searchTree.getLeftChild()) && Objects.isNull(searchTree.getRightChild())) {
searchTree.setBalanceNumber(0);
}
if (Objects.nonNull(searchTree.getLeftChild()) && Objects.nonNull(searchTree.getRightChild())) {
searchTree.setBalanceNumber(searchTree.getLeftChild().getHeight() - searchTree.getRightChild().getHeight());
}
}
if (Objects.nonNull(searchTree.getLeftChild())) {
countBalanceNumber(searchTree.getLeftChild(), max, searchTree, 1);
}
if (Objects.nonNull(searchTree.getRightChild())) {
countBalanceNumber(searchTree.getRightChild(), max, searchTree, 2);
}
if (Math.abs(searchTree.getBalanceNumber()) >= Math.abs(max.max)) {
if (Math.abs(searchTree.getBalanceNumber()) == Math.abs(max.max) && max.childTree == null) {
max.childTree = searchTree;
max.fatherTree = fatherTree;
max.flag = type;
max.max = searchTree.getBalanceNumber();
}
if (Math.abs(searchTree.getBalanceNumber()) > Math.abs(max.max)) {
max.childTree = searchTree;
max.fatherTree = fatherTree;
max.flag = type;
max.max = searchTree.getBalanceNumber();
}
}
}
public static SearchTree buildTree(SearchTree searchTree, Integer value) {
if (Objects.isNull(searchTree)) {
searchTree = new SearchTree();
}
if (Objects.isNull(searchTree.getValue())) {
searchTree.setValue(value);
return searchTree;
}
if (value >= searchTree.getValue()) {
if (Objects.isNull(searchTree.getRightChild())) {
SearchTree searchTree1 = new SearchTree();
searchTree1.setValue(value);
searchTree.setRightChild(searchTree1);
} else {
buildTree(searchTree.getRightChild(), value);
}
} else {
if (Objects.isNull(searchTree.getLeftChild())) {
SearchTree searchTree1 = new SearchTree();
searchTree1.setValue(value);
searchTree.setLeftChild(searchTree1);
} else {
buildTree(searchTree.getLeftChild(), value);
}
}
return searchTree;
}
public static void main(String[] args) {
// int[] a = new int[]{2, 4, 1, 3, 5, 10, 9, 8};
int[] a = new int[]{2, 4, 1, 3, 5, 10, 9, 8, 6, 7};
SearchTree searchTree = new SearchTree();
for (int i = 0; i < a.length; i++) {
searchTree = buildTree(searchTree, a[i]);
countHeight(searchTree);
MaxNumber maxNumber = checkBalance(searchTree);
SearchTree searchTree1 = maxNumber.childTree;
if (Math.abs(searchTree1.getBalanceNumber()) >= 2) {
searchTree1 = rotate(searchTree1);
if (maxNumber.flag == 0) {
maxNumber.fatherTree = searchTree1;
searchTree = searchTree1;
} else if (maxNumber.flag == 1) {
maxNumber.fatherTree.setLeftChild(searchTree1);
} else if (maxNumber.flag == 2) {
maxNumber.fatherTree.setRightChild(searchTree1);
}
countHeight(searchTree);
}
}
System.out.println("最終為\n" + Json.toJson(searchTree));
}
}以序列2, 4, 1, 3, 5, 10, 9, 8, 6, 7為例,構造的平衡二叉搜索樹結構為
{
"value": 4,
"left_child": {
"value": 2,
"left_child": {
"value": 1,
"left_child": null,
"right_child": null,
"balance_number": 0,
"height": 1
},
"right_child": {
"value": 3,
"left_child": null,
"right_child": null,
"balance_number": 0,
"height": 1
},
"balance_number": 0,
"height": 2
},
"right_child": {
"value": 8,
"left_child": {
"value": 6,
"left_child": {
"value": 5,
"left_child": null,
"right_child": null,
"balance_number": 0,
"height": 1
},
"right_child": {
"value": 7,
"left_child": null,
"right_child": null,
"balance_number": 0,
"height": 1
},
"balance_number": 0,
"height": 2
},
"right_child": {
"value": 10,
"left_child": {
"value": 9,
"left_child": null,
"right_child": null,
"balance_number": 0,
"height": 1
},
"right_child": null,
"balance_number": 1,
"height": 2
},
"balance_number": 0,
"height": 3
},
"balance_number": -1,
"height": 4
}到此,相信大家對“Java平衡二叉樹怎么實現”有了更深的了解,不妨來實際操作一番吧!這里是億速云網站,更多相關內容可以進入相關頻道進行查詢,關注我們,繼續學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。