您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
小編給大家分享一下Java二叉搜索樹增、插、刪、創的示例分析,希望大家閱讀完這篇文章之后都有所收獲,下面讓我們一起去探討吧!
二叉搜索樹又稱二叉排序樹,它或者是一棵空樹**,或者是具有以下性質的二叉樹:
若它的左子樹不為空,則左子樹上所有節點的值都小于根節點的值
若它的右子樹不為空,則右子樹上所有節點的值都大于根節點的值
它的左右子樹也分別為二叉搜索樹
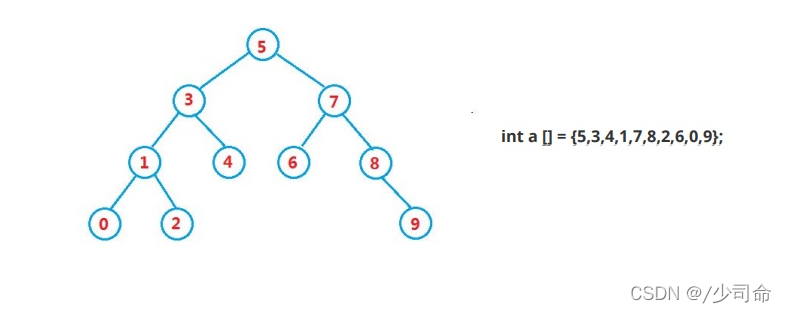
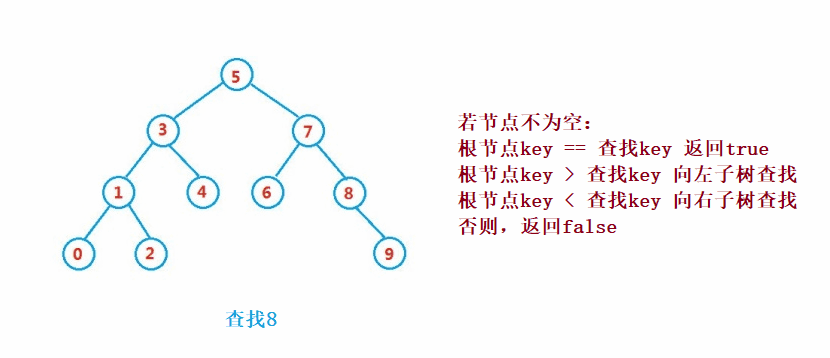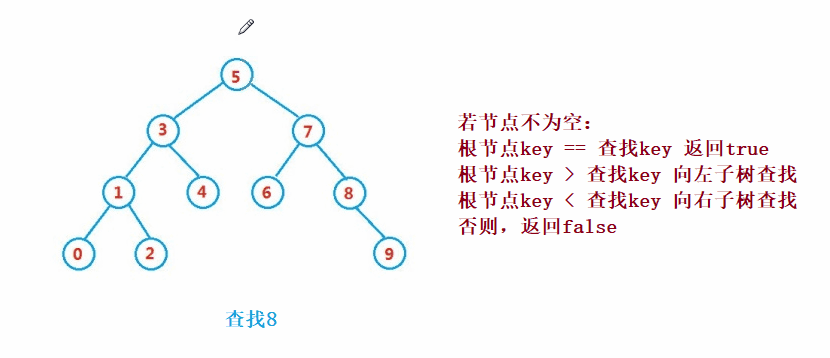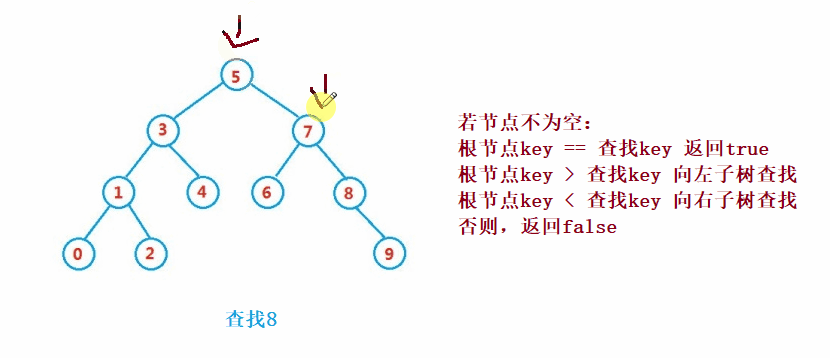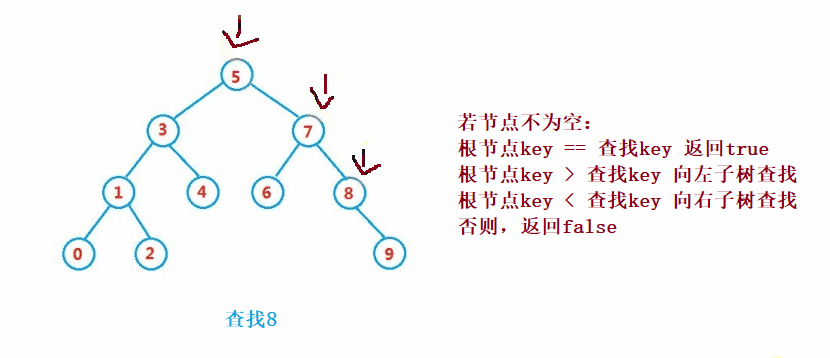
二叉搜索樹的查找類似于二分法查找
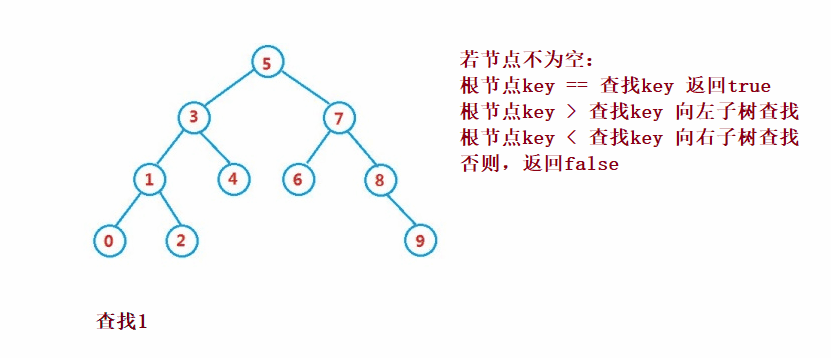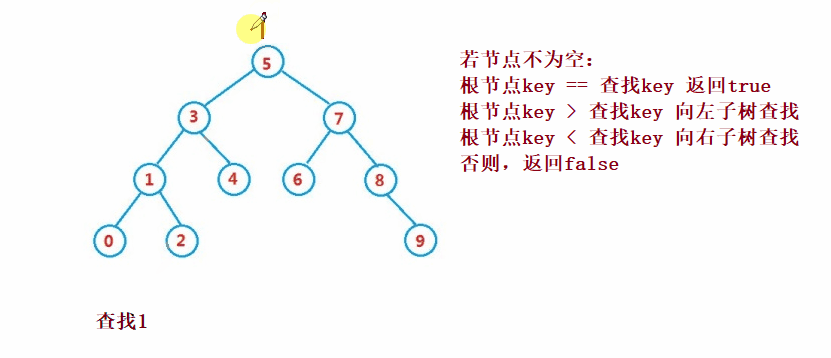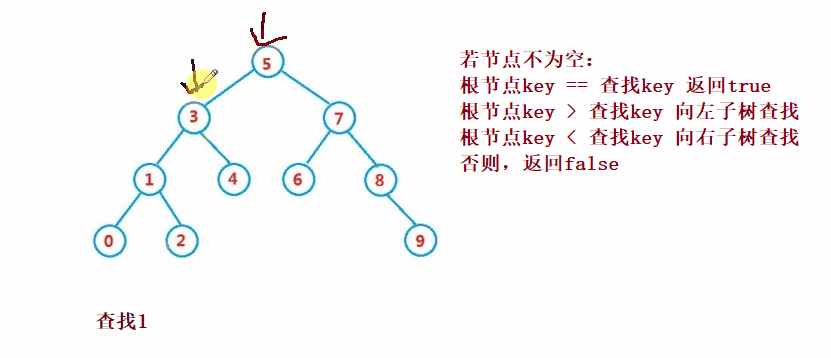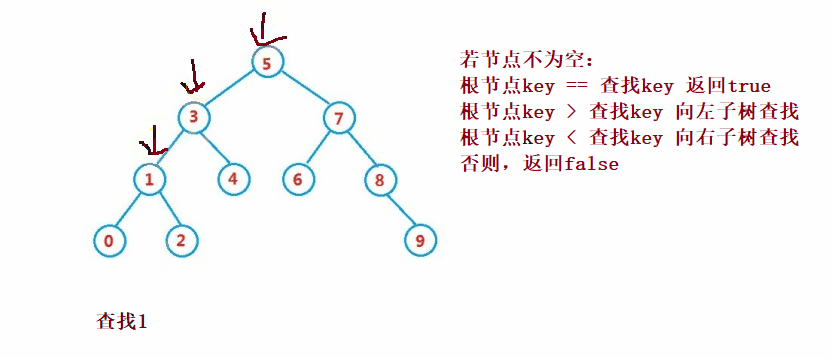
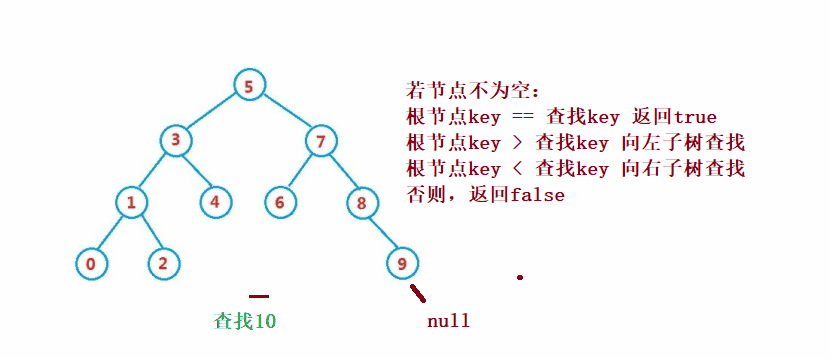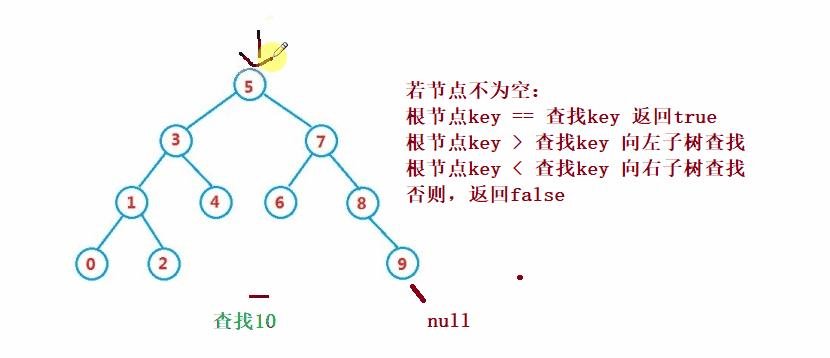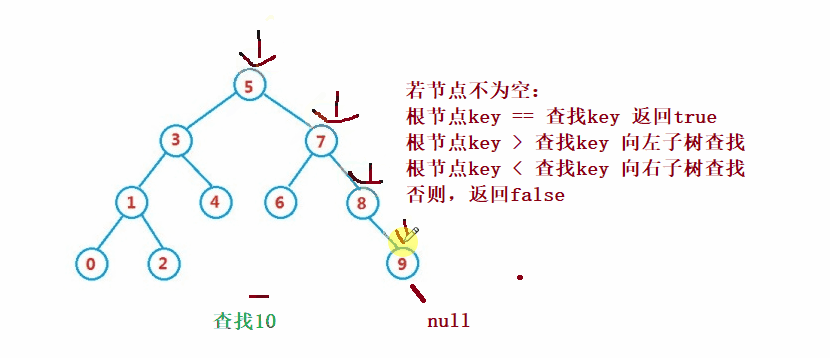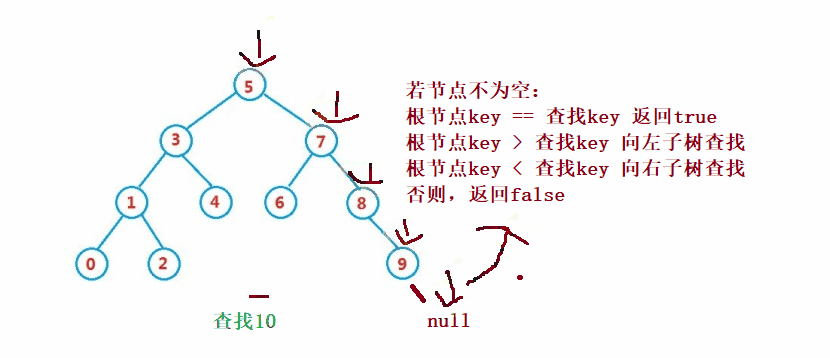
public Node search(int key) {
Node cur = root;
while (cur != null) {
if(cur.val == key) {
return cur;
}else if(cur.val < key) {
cur = cur.right;
}else {
cur = cur.left;
}
}
return null;
}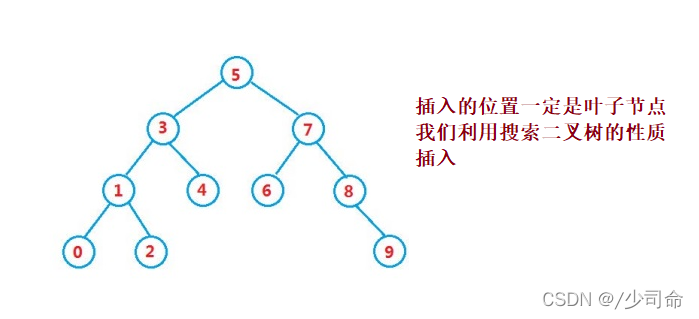
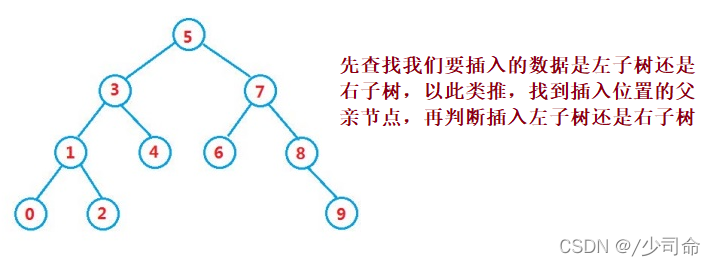
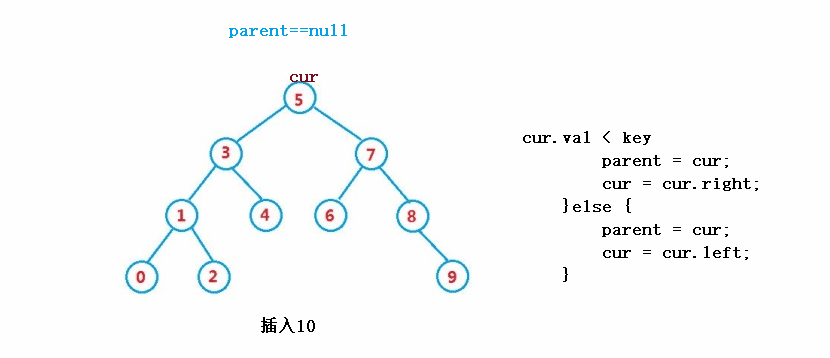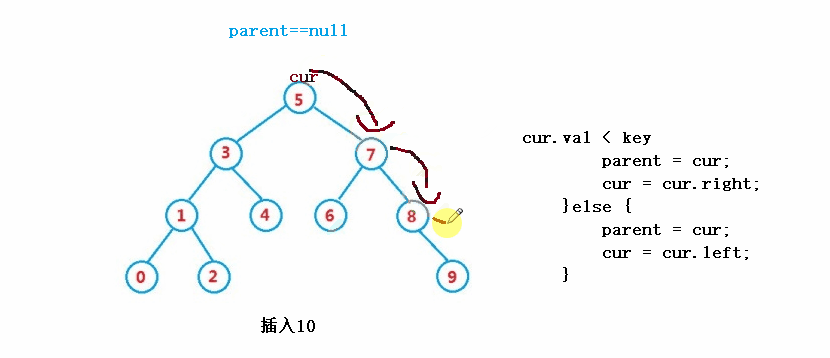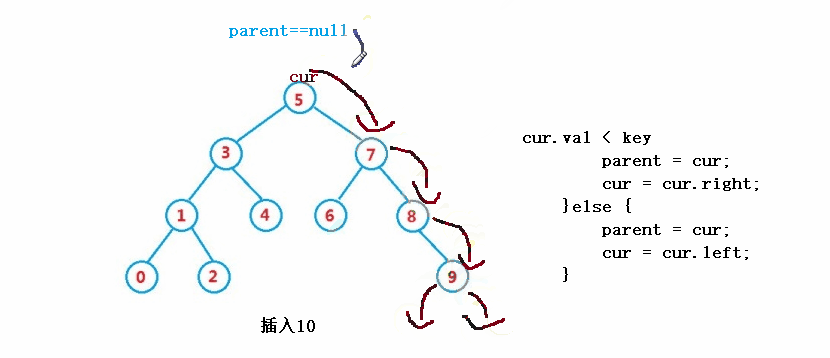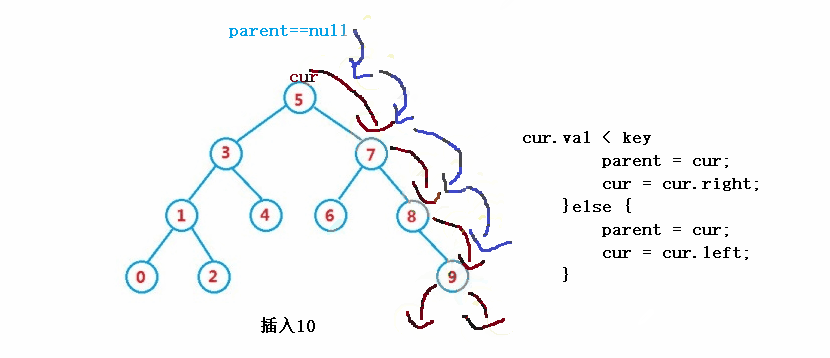
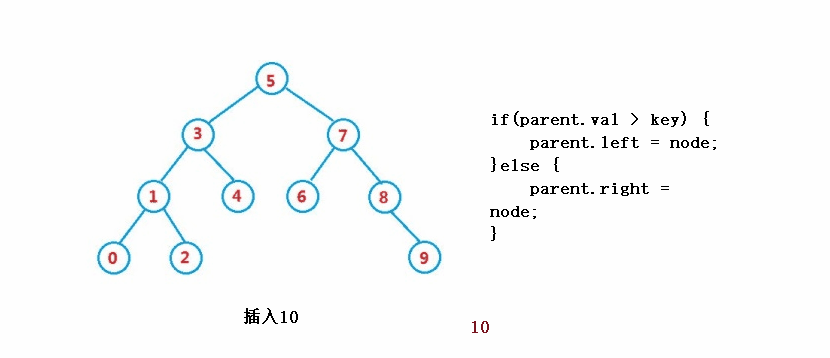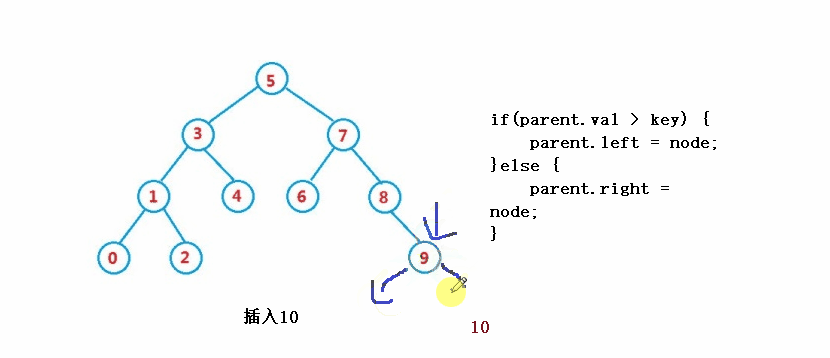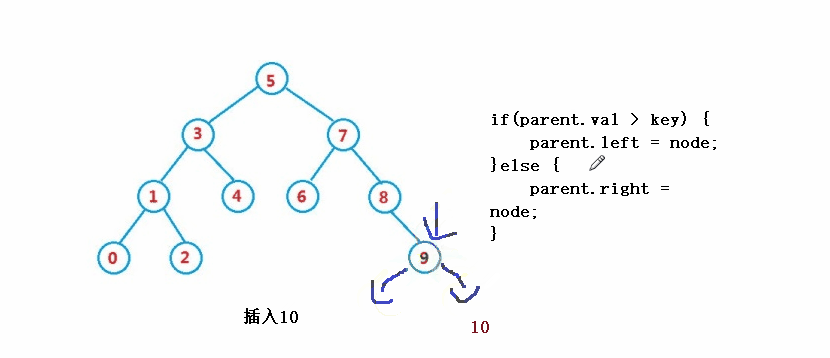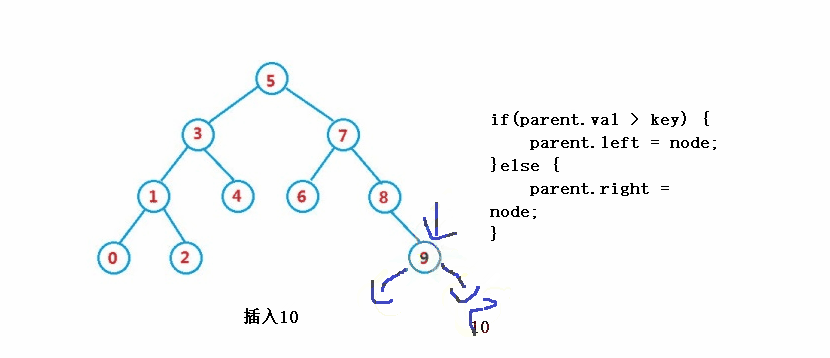
public boolean insert(int key) {
Node node = new Node(key);
if(root == null) {
root = node;
return true;
}
Node cur = root;
Node parent = null;
while(cur != null) {
if(cur.val == key) {
return false;
}else if(cur.val < key) {
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
//parent
if(parent.val > key) {
parent.left = node;
}else {
parent.right = node;
}
return true;
}刪除操作較為復雜,但理解了其原理還是比較容易
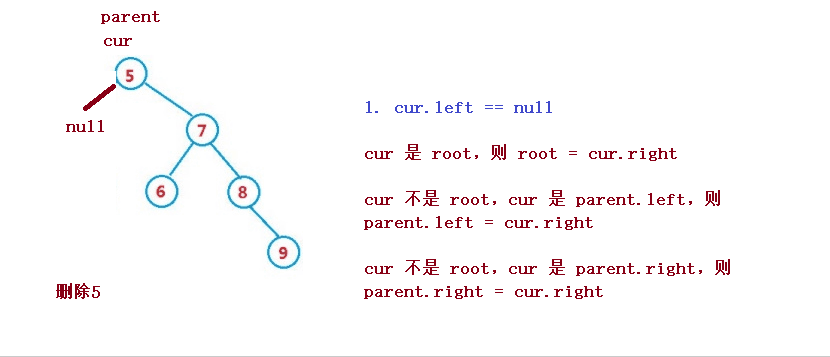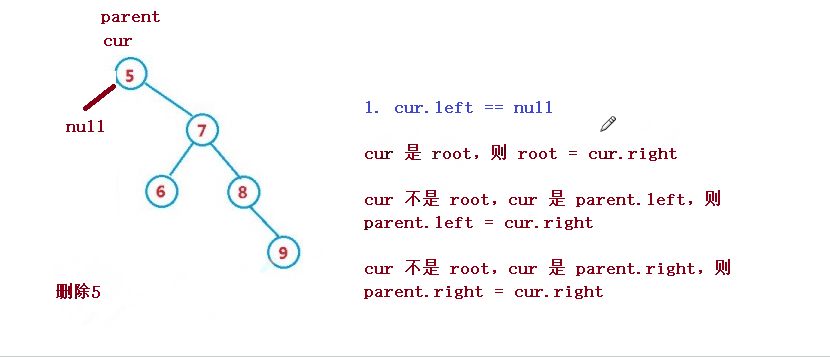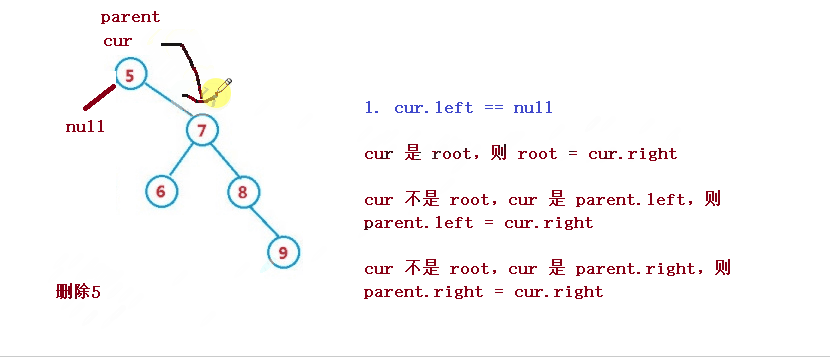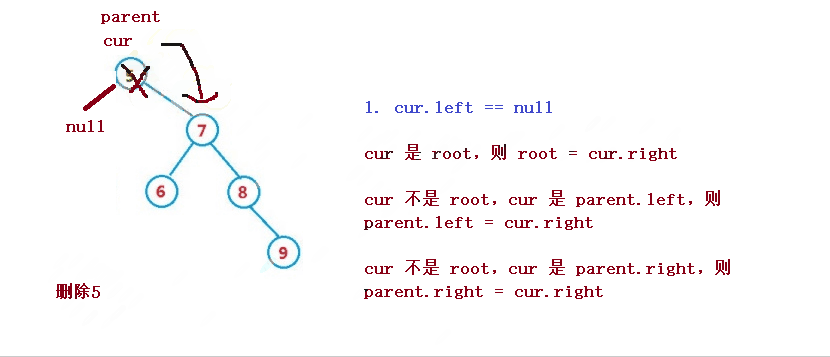
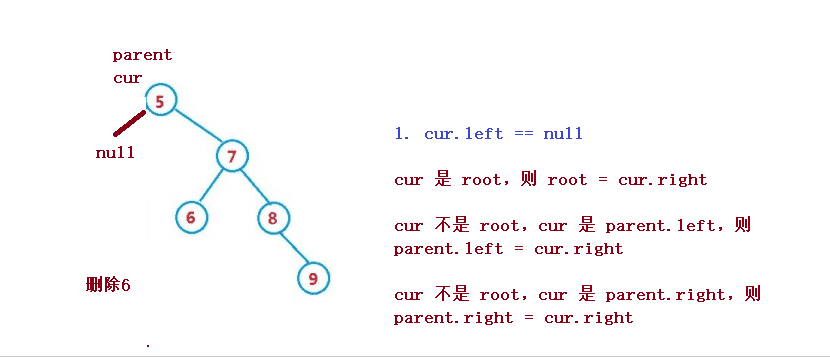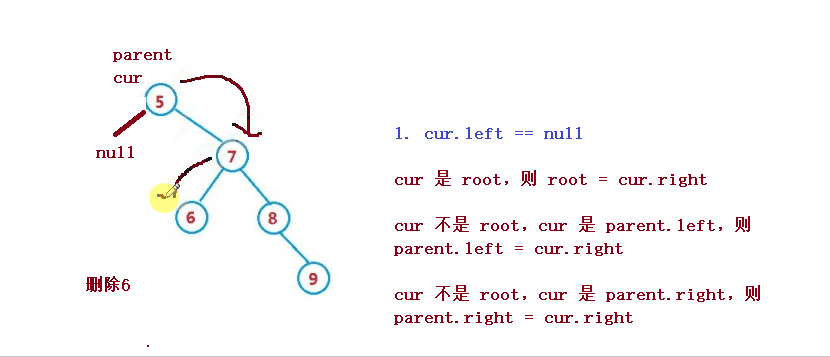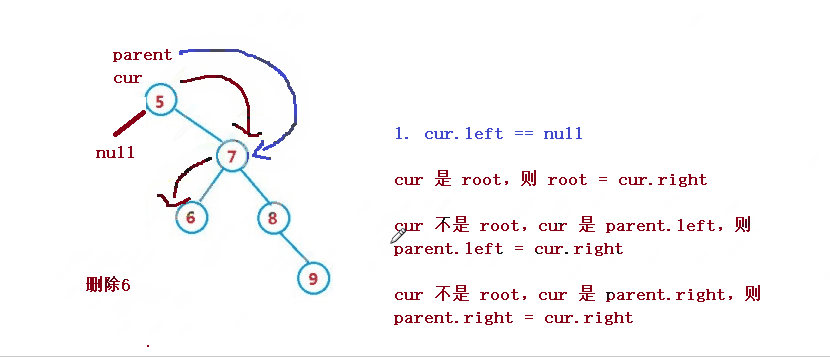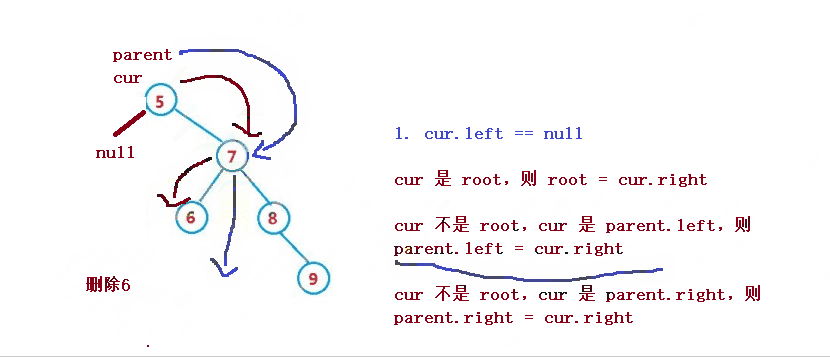
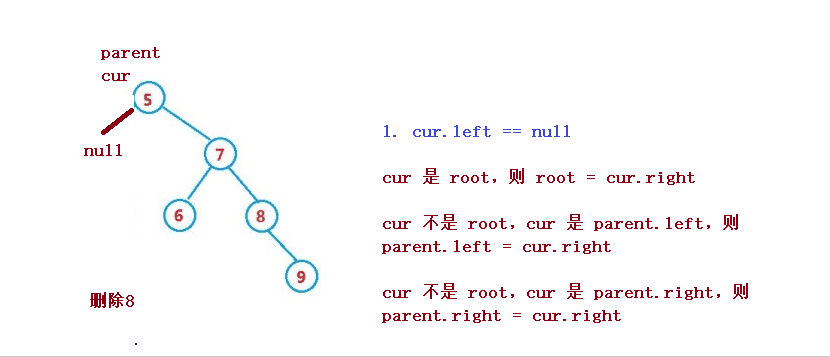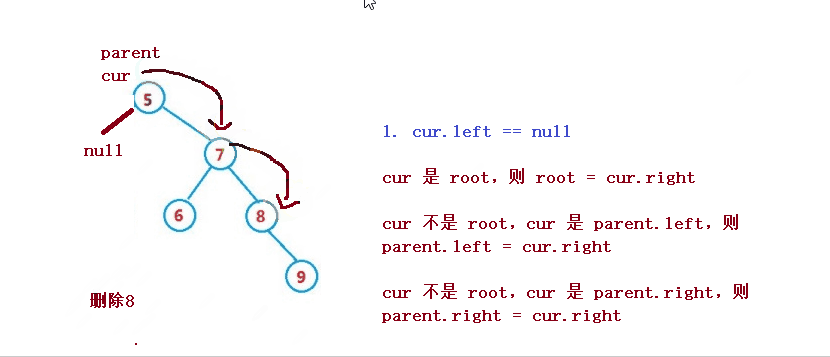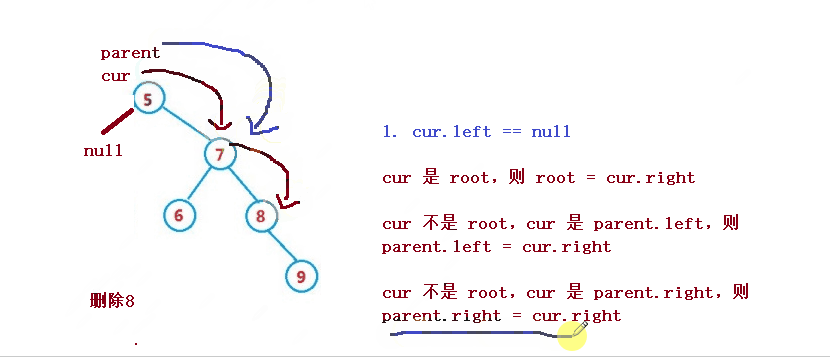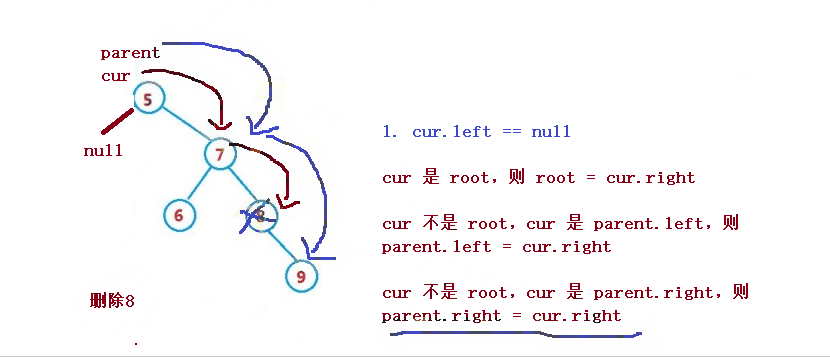
設待刪除結點為 cur, 待刪除結點的雙親結點為 parent
1. cur 是 root,則 root = cur.right
2. cur 不是 root,cur 是 parent.left,則 parent.left = cur.right
3. cur 不是 root,cur 是 parent.right,則 parent.right = cur.right
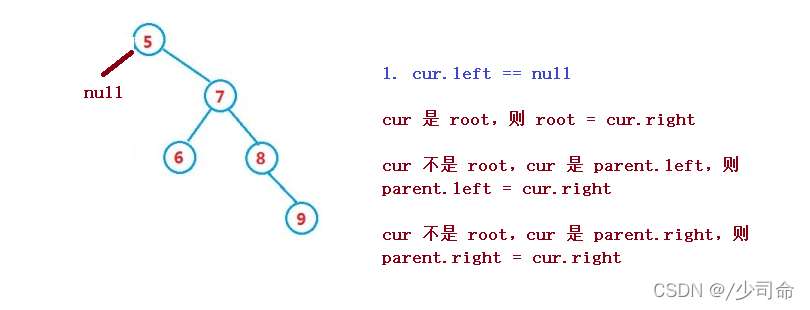
1. cur 是 root,則 root = cur.left
2. cur 不是 root,cur 是 parent.left,則 parent.left = cur.left
3. cur 不是 root,cur 是 parent.right,則 parent.right = cur.left
第二種情況和第一種情況相同,只是方向相反,這里不再畫圖
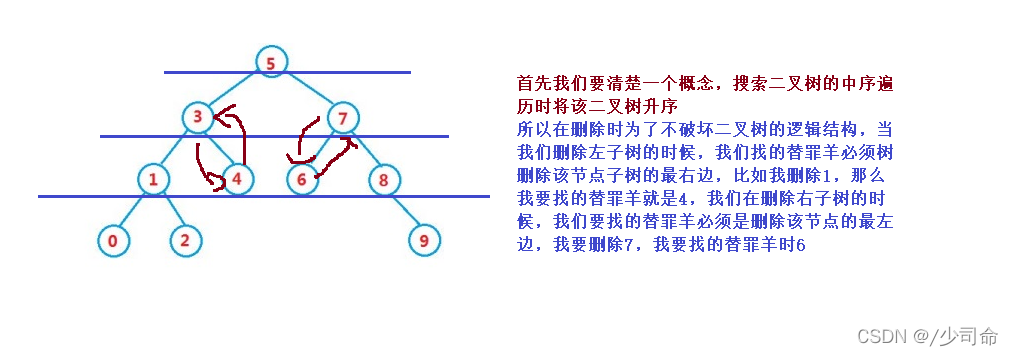
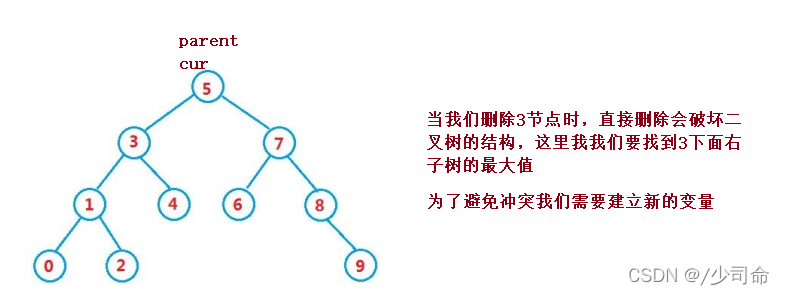
需要使用替換法進行刪除,即在它的右子樹中尋找中序下的第一個結點(關鍵碼最小),用它的值填補到被刪除節點中,再來處理該結點的刪除問題
當我們在左右子樹都不為空的情況下進行刪除,刪除該節點會破壞樹的結構,因此用替罪羊的方法來解決,實際刪除的過程還是上面的兩種情況,這里還是用到了搜索二叉樹的性質
public void remove(Node parent,Node cur) {
if(cur.left == null) {
if(cur == root) {
root = cur.right;
}else if(cur == parent.left) {
parent.left = cur.right;
}else {
parent.right = cur.right;
}
}else if(cur.right == null) {
if(cur == root) {
root = cur.left;
}else if(cur == parent.left) {
parent.left = cur.left;
}else {
parent.right = cur.left;
}
}else {
Node targetParent = cur;
Node target = cur.right;
while (target.left != null) {
targetParent = target;
target = target.left;
}
cur.val = target.val;
if(target == targetParent.left) {
targetParent.left = target.right;
}else {
targetParent.right = target.right;
}
}
}
public void removeKey(int key) {
if(root == null) {
return;
}
Node cur = root;
Node parent = null;
while (cur != null) {
if(cur.val == key) {
remove(parent,cur);
return;
}else if(cur.val < key){
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
}插入和刪除操作都必須先查找,查找效率代表了二叉搜索樹中各個操作的性能。
對有n個結點的二叉搜索樹,若每個元素查找的概率相等,則二叉搜索樹平均查找長度是結點在二叉搜索樹的深度 的函數,即結點越深,則比較次數越多。
但對于同一個關鍵碼集合,如果各關鍵碼插入的次序不同,可能得到不同結構的二叉搜索樹:
最優情況下,二叉搜索樹為完全二叉樹,其平均比較次數為:
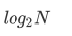
最差情況下,二叉搜索樹退化為單支樹,其平均比較次數為:

public class TextDemo {
public static class Node {
public int val;
public Node left;
public Node right;
public Node (int val) {
this.val = val;
}
}
public Node root;
/**
* 查找
* @param key
*/
public Node search(int key) {
Node cur = root;
while (cur != null) {
if(cur.val == key) {
return cur;
}else if(cur.val < key) {
cur = cur.right;
}else {
cur = cur.left;
}
}
return null;
}
/**
*
* @param key
* @return
*/
public boolean insert(int key) {
Node node = new Node(key);
if(root == null) {
root = node;
return true;
}
Node cur = root;
Node parent = null;
while(cur != null) {
if(cur.val == key) {
return false;
}else if(cur.val < key) {
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
//parent
if(parent.val > key) {
parent.left = node;
}else {
parent.right = node;
}
return true;
}
public void remove(Node parent,Node cur) {
if(cur.left == null) {
if(cur == root) {
root = cur.right;
}else if(cur == parent.left) {
parent.left = cur.right;
}else {
parent.right = cur.right;
}
}else if(cur.right == null) {
if(cur == root) {
root = cur.left;
}else if(cur == parent.left) {
parent.left = cur.left;
}else {
parent.right = cur.left;
}
}else {
Node targetParent = cur;
Node target = cur.right;
while (target.left != null) {
targetParent = target;
target = target.left;
}
cur.val = target.val;
if(target == targetParent.left) {
targetParent.left = target.right;
}else {
targetParent.right = target.right;
}
}
}
public void removeKey(int key) {
if(root == null) {
return;
}
Node cur = root;
Node parent = null;
while (cur != null) {
if(cur.val == key) {
remove(parent,cur);
return;
}else if(cur.val < key){
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
}
}看完了這篇文章,相信你對“Java二叉搜索樹增、插、刪、創的示例分析”有了一定的了解,如果想了解更多相關知識,歡迎關注億速云行業資訊頻道,感謝各位的閱讀!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。