您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
海明碼(Hamming Code)是一個可以有多個校驗位,具有檢測并糾正一位錯誤代碼的糾錯碼,所以它也僅用于信道特性比較好的環境中,如以太網中,因為如果信道特性不好的情況下,出現的錯誤通常不是一位。
海明碼的檢錯、糾錯基本思想是將有效信息按某種規律分成若干組,每組安排一個校驗位進行奇偶性測試,然后產生多位檢測信息,并從中得出具體的出錯位置,最后通過對錯誤位取反(原來是1就變成0,原來是0就變成1)來將其糾正。
根據海明碼的糾錯原理,得出了:
m+k+1<=2K
其中:m表示有效的信息位數;k表示用于糾錯的位數。滿足了上面的公式,才能進行糾錯。
舉例說明,假設有一組信息碼為:1101 0111 0,如何計算海明碼?
一、確定糾錯用的冗余位數
M=9,那么,9+k+1<=2k,由此得出k=4,也就是說要在原始有效信息位填充4bit二進位。
二、冗余填充位的計算
4個bit的冗余位按照海明碼的原理要填充在2n位上,即1、2、4、8……位上。由此得出如下的表格
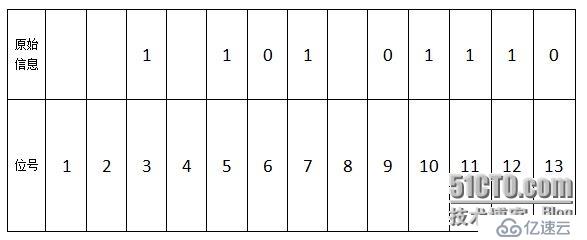
將信息位與冗余位間的關系整理成一張表格如下。
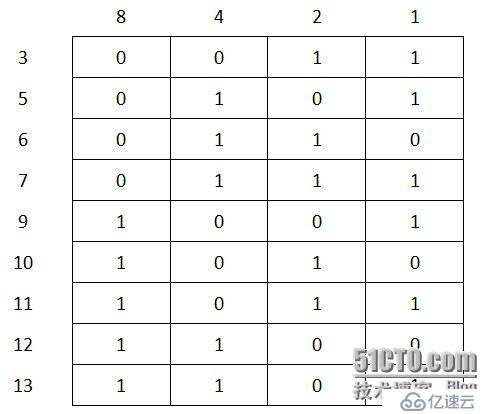
由此得出:
第1個冗余位由3、5、7、9、11、13參與校驗
第2個冗余位由3、6、7、10、11參與校驗
第4個冗余位由5、6、7、12、13參與校驗
第8個冗余位由9、10、11、12、13參與校驗
如果全部按偶校驗計算得出如下圖結果:
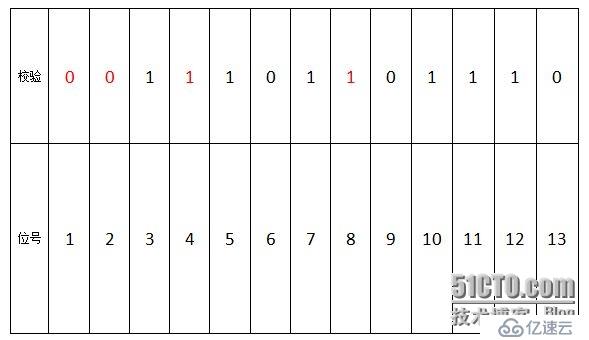
可以這樣理解:
第1bit位:B1⊕B3⊕B5⊕B7⊕B9⊕B11⊕B13=0⊕1⊕1⊕1⊕0⊕1⊕0=0
第2bit位:B2⊕B3⊕B6⊕B7⊕B10⊕B11 =0⊕1⊕0⊕1⊕1⊕1=0
第4bit位:B4⊕B5⊕B6⊕B7⊕B12⊕B13 =1⊕1⊕0⊕1⊕1⊕0=0
第8bit位:B8⊕B9⊕B10⊕B11⊕B12⊕B13 =1⊕0⊕1⊕1⊕1⊕0=0
我們稱上面的4個式子為監督關系式。
也就是說,校驗與原有的信息做異或運算按偶校驗計算得出的結果全部是0 。
因此,這4個bit的冗余位是:0011
三、信息校驗
假設有一位數據出錯了,我們這里假設是第10位在傳輸過程中由1變成了0,出錯了,這樣上面的4個監督關系式就會發生變化,變成如下:
第1bit位:B1⊕B3⊕B5⊕B7⊕B9⊕B11⊕B13=0⊕1⊕1⊕1⊕0⊕1⊕0=0
第2bit位:B2⊕B3⊕B6⊕B7⊕B10⊕B11 =0⊕1⊕0⊕1⊕0⊕1=1
第4bit位:B4⊕B5⊕B6⊕B7⊕B12⊕B13 =1⊕1⊕0⊕1⊕1⊕0=0
第8bit位:B8⊕B9⊕B10⊕B11⊕B12⊕B13 =1⊕0⊕0⊕1⊕1⊕0=1
由此可以看出,1和4式沒有錯,而2和8出現了錯誤,由此B3、B6、B7、B10、B11、B9、B12、B13可能是出錯位,但是從1和4位可以看出正確的位是:B3、B5、B7、B9、B11、B13、B6、B12,從可能出錯的位中把正確的去掉,就剩下了B3、B6、B7、B10、B11、B9、B12、B13(紅色字是去掉的位),這樣就僅剩下第10位了,這樣我們把10進行反轉就得到了正確的信息了。
更簡單的方法是由高位往低位寫(即由第8位寫到第一位)結果是1010,轉換為10進制數為10,就是第10位出錯了
有這樣一道題:
使用海明碼進行前向糾錯,如果冗余為4位,那么信息位最多可以用到多少位?假定碼字位a6 a5 a4 a3 a2 a1 a0,并且有下面的監督關系式:
S2=a2+a4+a5+a6
S1=a1+a3+a5+a6
S0=a0+a3+a4+a6
若S2S1S0=110,則表示出錯位是哪一位?
答案:可以用到11位;a5位出錯
寫得不好,請指教!!!!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。