您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要講解了“怎么理解java圖的對象化描述”,文中的講解內容簡單清晰,易于學習與理解,下面請大家跟著小編的思路慢慢深入,一起來研究和學習“怎么理解java圖的對象化描述”吧!
對于圖來說,我一直以來都似懂非懂
懂的是圖的含義,不懂的是圖具體的實現
對于當前各大廠面試的圖題,不外乎以下幾點:
深度優先搜索、廣度優先搜索:DFS、BFS最小生成樹:Kruskal、Prim最短路徑:Dijkstra、Dijkstra加強堆版拓撲排序:TopologicalSort
這幾個算法其實聽起來不太難懂,但真正寫代碼的時候會發現一個事情,傻逼圖的邊和點太難描述,導致我們寫著寫著人就沒了,繞進去出不來了。
圖是我們現實生活中連接關系的抽象,例如朋友圈、微博的關注關系。
對于圖來說,分為有向圖和無向圖,如下圖所示:

我們可以看出來,有向圖代表只能從一個頂點到達另一個頂點,而無向圖代表兩個頂點之間可以相互到達。
圖1中,V4到達V1,而V1無法到達V4
圖2中,V4到達V1,V1也可以到達V4
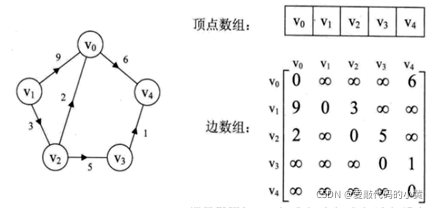
當然,還有一種圖的形式,叫做:帶權圖(主要用來做一些路程、路費的計算),如下圖所示:
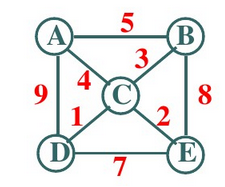
我們在刷題的時候,題目給我們的樣例經常是這種的:743. 網絡延遲時間
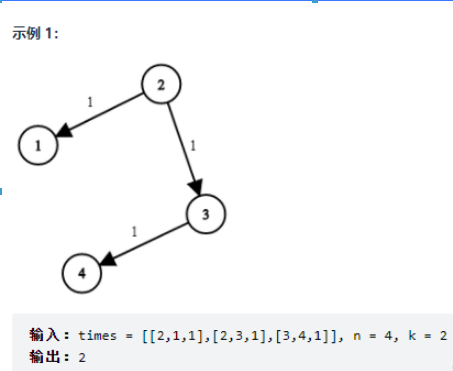
題目會給我們一個二維的矩陣,一行矩陣有三個數字,分別是:起始點、終止點、權重
如何將這個二維的矩陣表示出來,成為了我們在做圖題目中比較困難的一件事
本文將直接使用一種特殊的表示形式來解決這個難題,我們先從最基本的 鄰接矩陣 和 鄰接表 表示開始
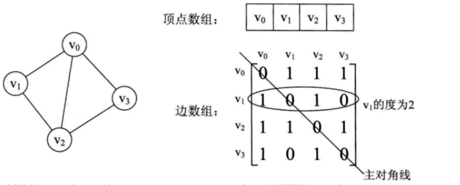
鄰接矩陣是表示圖中頂點之間相鄰關系的矩陣。
對于無向圖的鄰接矩陣:對稱矩陣:int[][]
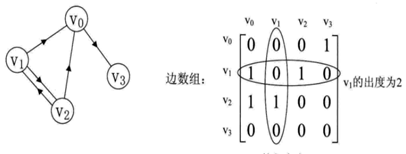
有向圖的鄰接矩陣:各行之和是出度,各列之和是入度
帶權圖的鄰接矩陣
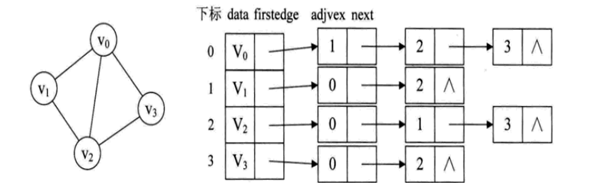
鄰接表是一種鏈式存儲結構,類似于鏈表數組。
無向圖的鄰接表:HashMap<Integer, ArrayList<Integer>>
我們思考,上述兩個方法對于圖的表示形象嘛?
雖然有的題目在用矩陣表示的時候,做起來很舒服,但我們想一想,當我們求最小生成樹時,利用邊的連接解鎖點時,用矩陣會
不會感覺很抽象難懂,所示,我們要自定義一個圖的表示方法,來增強我們對圖的理解
對于圖來說,我們想一想主要包括什么?
圖是由點和邊組成的一個結構,也就是我們想要勾畫一個圖,必須有:點、邊
點的描述:
點的值:int value
鄰接的點:ArrayList<Node> nexts
鄰接的邊:ArrayList<Edge> edges
入度:int in
出度:int out
public class Node {
public int value;
public int in;
public int out;
public ArrayList<Node> nexts;
public ArrayList<Edge> edges;
public Node(int value) {
this.value = value;
in = 0;
out = 0;
nexts = new ArrayList<>();
edges = new ArrayList<>();
}
}邊的描述:
來自哪里:Node from去往哪里:Node to邊的權重:int weight
public class Edge {
Node from;
Node to;
int weight;
public Edge(Node from, Node to, int weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
}圖的描述:
多個點的集合:HashMap<Integer, Node> nodes多個邊的集合:Set<Edge> edges
public class Graph {
public HashMap<Integer, Node> nodes;
public Set<Edge> edges;
public Graph() {
nodes = new HashMap<>();
edges = new HashSet<>();
}
}這里可能有疑問了,你這樣寫雖然形象,但是怎么進行轉化呢?
別急,下面我們就進行轉化。
public static Graph createGraph(int[][] matrix) {
// 初始化一個圖
Graph graph = new Graph();
for (int[] arr : matrix) {
// 來的點
int from = arr[0];
// 去的點
int to = arr[1];
// 權重
int value = arr[2];
// 生成相對應的點
Node fromNode = new Node(from);
Node toNode = new Node(to);
// 查看當前有沒有這個點的信息
if (!graph.nodes.containsKey(from)) {
graph.nodes.put(from, fromNode);
}
if (!graph.nodes.containsKey(to)) {
graph.nodes.put(to, toNode);
}
// 生成一個邊(這里的邊是有向邊)
Edge edge = new Edge(fromNode, toNode, value);
// 點里面加入邊
graph.nodes.get(from).edges.add(edge);
// 點里面加入下一個點
graph.nodes.get(from).nexts.add(toNode);
// 點里面加入入度和出度
graph.nodes.get(from).out++;
graph.nodes.get(to).in++;
// 圖里面加入邊
graph.edges.add(edge);
}
return graph;
}當我們轉化完的時候,進行測試:
public static void main(String[] args) {
int[][] arr = new int[][]{{2, 1, 1}, {2, 3, 1}, {3, 4, 1}};
Graph graph = createGraph(arr);
// 從2開始的邊有哪些
List<Edge> edgeList = graph.nodes.get(2).edges;
for (Edge edge : edgeList) {
System.out.println("從" + edge.from.value + "---->" + edge.to.value + "權值為" + edge.weight);
}
}最終結果:
從2---->1權值為1
從2---->3權值為1
以后我們在做題的時候,都可以保存此轉化代碼,直接進行調用即可
簡單形象的描繪了我們的圖
圖經常用在以下地方:
深度優先搜索、廣度優先搜索:DFS、BFS
最小生成樹:Kruskal、Prim
最短路徑:Dijkstra、Dijkstra加強堆版
拓撲排序:TopologicalSort
感謝各位的閱讀,以上就是“怎么理解java圖的對象化描述”的內容了,經過本文的學習后,相信大家對怎么理解java圖的對象化描述這一問題有了更深刻的體會,具體使用情況還需要大家實踐驗證。這里是億速云,小編將為大家推送更多相關知識點的文章,歡迎關注!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。