您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容介紹了“如何使用Python計算雙重差分模型DID及其對應P值”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!
1. DID(Differences-in-Differences)定義
2. DID模型形式
3. OLS多項式擬合
雙重差分法,其主要被用于社會學中的政策效果評估。這種方法需要兩個「差異」數據。一個是干預前后的「差異」,這個是自身實驗前后的差異。另外一個是干預組與對照組的「差異」。DID利用這兩個「差異」的差異來推算干預的效果。因此,顧名思義叫做雙重差分法。
其原理是基于一個反事實的框架來評估政策發生和不發生這兩種情況下被觀測因素y的變化。如果一個外生的政策沖擊將樣本分為兩組:受政策干預的Treat組和未受政策干預的Control組(在政策沖擊前,Treat組和Control組的y沒有顯著差異)。那么,可以將Control組在政策發生前后y的變化看作Treat組未受政策沖擊時的狀況(反事實的結果)。通過比較Treat組y的變化(D1)以及Control組y的變化(D2),就可以得到政策沖擊的實際效果(DD=D1-D2)。
注意:只有在滿足“政策沖擊前Treat組和Control組的y沒有顯著差異”(即平行性假定)的條件下,得到的雙重差分估計量才是無偏的。
如下圖所示:
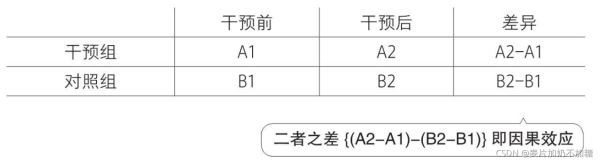
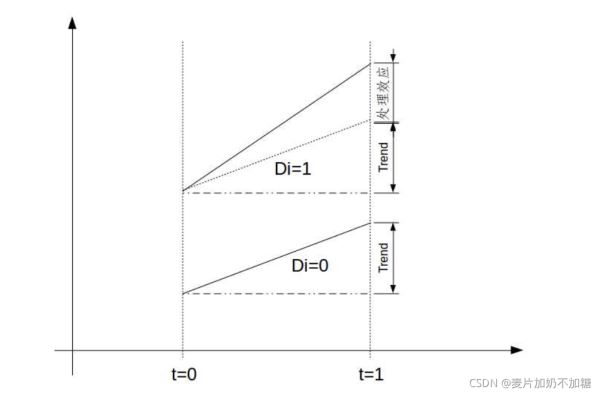
干預組實驗前為A1,實驗后為A2。對照組實驗前為B1,實驗后為B2。對于干預組實驗前后差異為A2-A1,對于對照組實驗后為B2-B1。兩者之差(A2-A1)-(B2-B1)即為DID結果,因果效應/處理效應。如下圖處理效應所代表的部分。
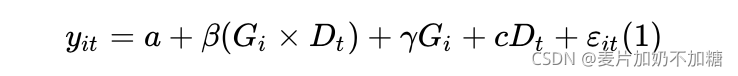
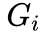 為分組虛擬變量(處理組=1,控制組=0);
為分組虛擬變量(處理組=1,控制組=0);
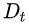 為分期虛擬變量(政策實施后=1,政策實施前=0);
為分期虛擬變量(政策實施后=1,政策實施前=0);
交互項 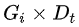 表示處理組在政策實施后的效應,其系數即為雙重差分模型重點考察的處理效應。
表示處理組在政策實施后的效應,其系數即為雙重差分模型重點考察的處理效應。
根據DID公式,我們可以通過使用多項式擬合的方法來求得DID及其P值。以下為Pyhton方法:使用statsmodels庫中ols方法,需要根據上述公式準備數據,t代表時間(干預前=0,干預后=1)、g代表分組(干預組=1,對照組=0)、還有一個是交叉項tg(計算其t*g即可)。
代碼如下:
import statsmodels.formula.api as smf
import pandas as pd
v1 =[0.367730,0.377147,0.352539,0.341864,0.29276,0.393443,0.374697,0.346989,0.385783,0.307801]
t1 = [0,0,0,0,1,0,0,0,0,1]
g1 =[1,1,1,1,1,0,0,0,0,0]
tg1 = [0,0,0,0,1,0,0,0,0,0]
aa = pd.DataFrame({'t1':t1,'g1':g1,'tg1':tg1,'v1':v1})
X = aa[['t1', 'g1','tg1']]
y = aa['v1']
est = smf.ols(formula='v1 ~ t1 + g1 + tg1', data=aa).fit()
y_pred = est.predict(X)
aa['v1_pred'] = y_pred
print(aa)
print(est.summary())
print(est.params)準備數據格式如下:
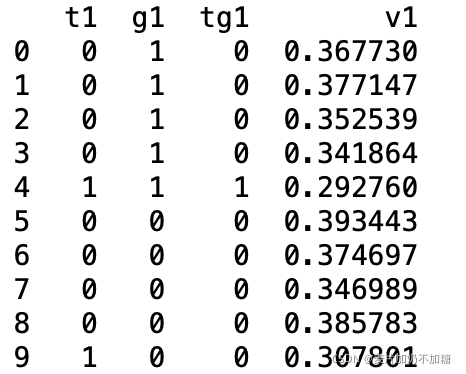
OLS結果Summary如下:
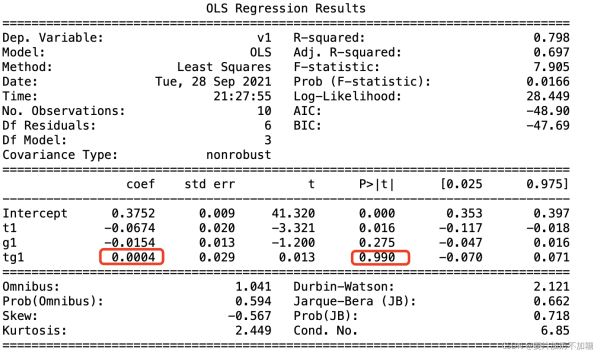
交叉項的系數就是DID結果,處理效應。P>| t |為其P值,小于0.05表示差異顯著。
“如何使用Python計算雙重差分模型DID及其對應P值”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站,小編將為大家輸出更多高質量的實用文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。