數據結構之樹的示例分析

這篇文章將為大家詳細講解有關數據結構之樹的示例分析，文章內容質量較高，因此小編分享給大家做個參考，希望大家閱讀完這篇文章后對相關知識有一定的了解。

數據結構樹簡介

一、樹簡介

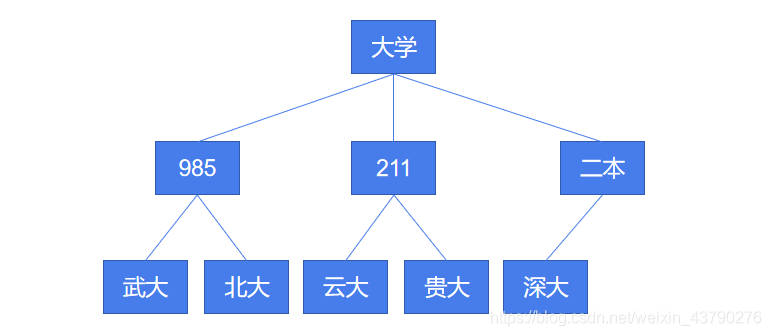
樹(Tree)是一種抽象的數據結構，是一個數據的集合，集合中的數據組成了一個樹狀結構。例如上圖，看起來像一棵倒掛的樹，根朝上葉朝下。

樹是由n(n>=0)個節點組成的具有層次關系的數據集合。當 n=0 時，樹中沒有節點，稱為空樹。當 n>0 時，有且僅有一個節點被稱為根節點(Root)，如果 n=1 ，樹只有根節點一個節點。如果 n>1 ，除根節點外，將其余的節點分成m(m>0)個互不相交的數據集合，這 m 個集合每一個都要滿足樹的結構(有且僅有一個根節點)，并且這 m 棵樹都“掛”在根節點上，如此遞歸下去，直到所有節點都“掛”到這棵樹上。其中，這 m 個集合構成的 m 棵樹都被稱為根節點的子樹。

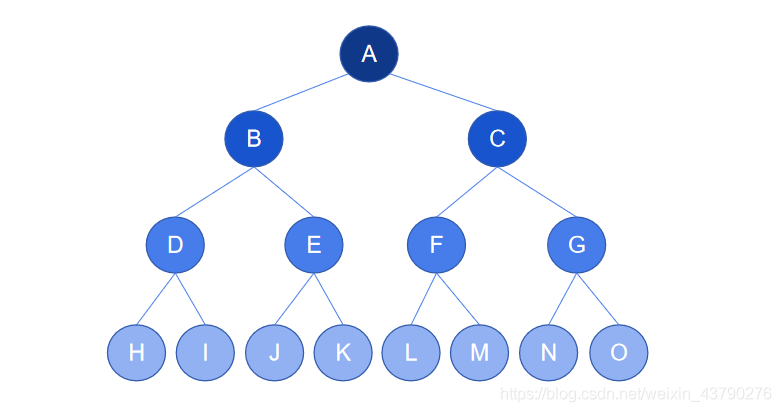
在理解樹的結構和定義時，需要運用到遞歸的思想。以下圖為例，樹的節點集合為 {A,B,C,D,E,F,G,H} ，n=8，根節點為 A ，除根節點 A 外，其余節點組成了兩個(m=2)集合(m1和m2)，m1集合為 {B,D,E} ，m2集合為 {C,F,G,H} 。在m1中，B 為m1的根節點，除 B 以外，其余節點組成兩個集合，集合 {D} 和集合 {E} ，{D} 和 {E} 都只有一個節點，分別構成一棵只有一個節點的樹，它們“掛”在m1的根節點 B 上，是 B 的子樹，m1構成一棵樹，“掛”在根節點 A 上，m1是 A 的子樹。同理，在m2中，C 為m2根節點，其余節點組成三個集合 {F} 、{G} 和 {H} ......

二、樹的術語

要理解樹這種數據結構，必須先理解一些常用的術語。

樹由一個一個的節點組成，節點是構成復雜數據結構的基本組成單位。

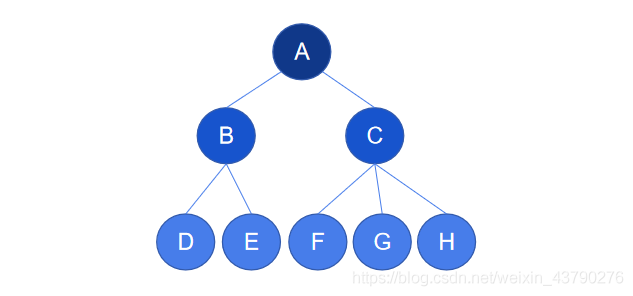
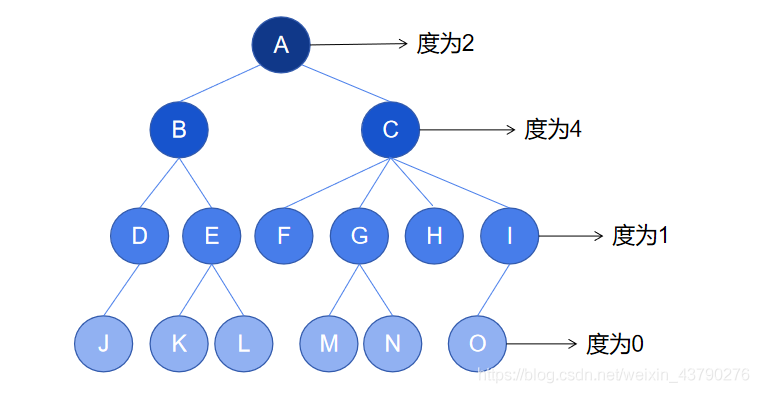
1. 子節點：又稱為孩子節點，一個節點所包含的子樹的根節點被稱為該節點的子節點。如下圖中，節點 B 有兩棵子樹，這兩棵子樹的根節點為 D 和 E ，所以 D 和 E 都是 B 的子節點。

2. 父節點：又稱為父親節點，如果一個節點有子節點，則這個節點被稱為其子節點的父節點。如下圖中，節點 B 有兩個子節點 D 和 E ，則 B 是 D 的父節點，也是 E 的父節點。

3. 兄弟節點：具有相同父節點的節點互稱為兄弟節點。下圖中的 D 和 E 就互為兄弟節點。

4. 堂兄弟節點：如果樹的兩個節點深度相同，但父節點不同，則它們互為堂兄弟節點。下圖中的 D與F，D與G，D與H，D與I 都是堂兄弟節點關系。

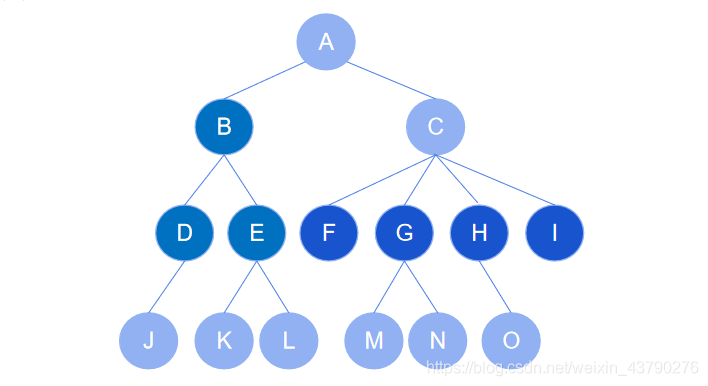
5. 節點的祖先：從根節點開始，依次找到某節點所經路徑上的所有節點都稱為該節點的祖先。如下圖中，節點 J 的祖先節點為 A,B,D 。

6. 節點的子孫：以某節點為根的子樹中，任一節點都稱為該節點的子孫。如下圖中，節點 C 的子孫有 F,G,H,I,M,N,O 。

7. 節點的層次：從根開始定義起，根為第1層，根的子節點為第2層，以此類推。如下圖中，根節點 A 在第1層，節點 M 在第4層。

8. 節點的深度：一個節點所處的層次稱為該節點的深度。如下圖中，根節點 A 的深度為1，節點 M 的深度為4 。(上面解釋堂兄弟節點時有用到節點的深度，現在可以回去看看)

9. 樹的深度：又稱為樹的高度，一棵樹中，最大的節點深度稱為樹的深度。如下圖中的樹深度為4。

關于深度和高度，有兩種定義方式，一種是將根節點的深度定義為0，另一種是將根節點的深度定義為1。但不管怎樣，每個深度為 k 的節點的子節點的深度都為 k+1 ，這是不變的。

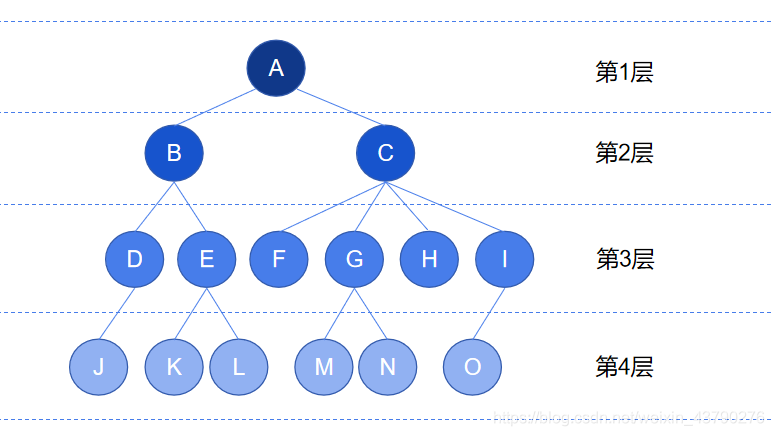
10. 節點的度：一個節點含有的子樹(或子節點)的個數稱為該節點的度。如下圖中， 根節點 A 的度為2，節點 C 的度為4，節點 I 的度為1，節點 O 的度為 0 。

11. 樹的度：一棵樹中，最大的節點度稱為樹的度。如下圖中，最大的節點度是4，則樹的度為4。

12. 葉節點：又稱為終端節點，度為零的節點被稱為葉節點。如下圖中，節點 F,H,J,K,L,M,N,O 都是葉節點。

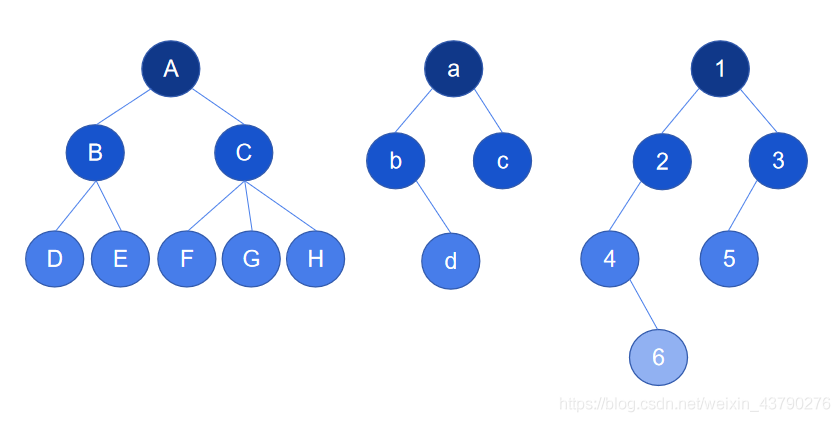
13. 森林：由m(m>=0)棵互不相交的樹構成的集合稱為森林。森林是從樹延伸出來的術語，森林里的樹一定是互不相交的。

三、樹的特點

通過對樹的定義和樹的術語進行介紹，基本可以理解樹這種數據結構了，總結起來，樹有以下特點。

1. 如果樹的節點數 n>0，根節點是唯一的，不可能存在多個根節點。

2. 沒有父節點的節點稱為根節點。根節點是沒有父節點的。

3. 每一個非根節點有且只有一個父節點。除了根節點外，其他所有節點都有父節點，并且同一個節點只有一個父節點，不可能有多個。

4. 每個節點有零個或多個子節點。

5. 除了根節點外，子節點可以分為多個不相交的子樹。這些子樹一定是互不相交的。

6. 每個深度為 k 的節點的子節點的深度都為 k+1 。

四、樹的分類

所有樹都滿足以上的特點，除此之外，一些樹還具有專有的特點。根據專有的特點，可以對樹進行分類。

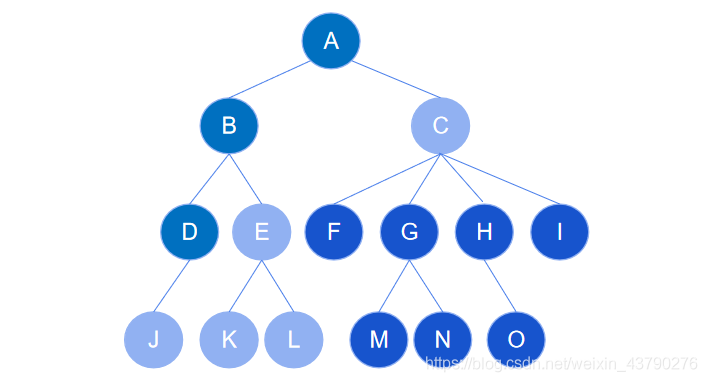
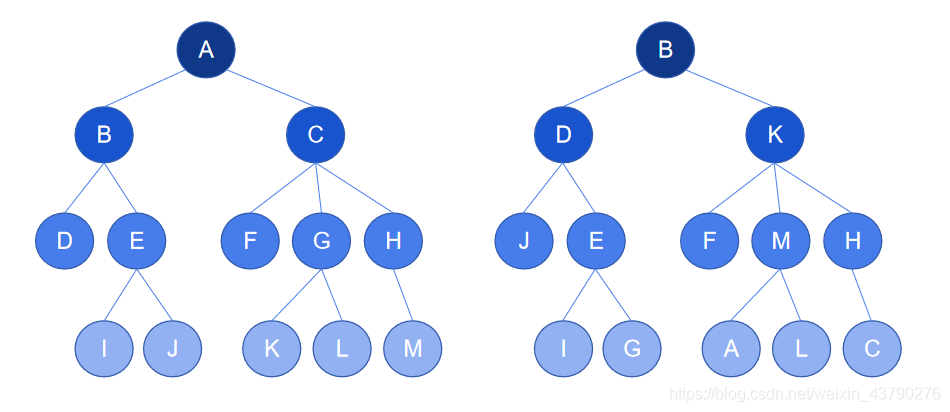
1. 無序樹：也稱為自由樹，樹中存在一個節點，節點的子節點之間沒有順序關系。如下圖中，右邊的樹是無序樹，從樹中取一個節點 D ，D 的子節點是節點 J 和節點 E，它們是沒有順序關系的，所以這是一棵無序樹。

2. 有序樹：樹中任意節點的子節點之間有順序關系。如下圖中，左邊的樹是有序樹，從樹中任意取一個節點 C，C 的子節點是 F,G,H ，它們是有順序關系的(字母順序)，所以這是一棵有序樹。

圖中的有序和無序以字母順序作為案例，實際應用中的“有序”并不限于字母順序、數字順序等，實際的有序主要是指“不能互換”。

無序樹的節點之間沒有順序關系，節點之間的關系不能通過代碼來模擬和控制，所以基本沒有實際的應用場景。

使用樹這種數據結構，基本都是使用有序樹，對于有序樹，又可以分為以下幾種。

1. 二叉樹：每個節點最多含有兩個子樹的樹稱為二叉樹，如下圖。二叉樹是最常用的樹結構，可以對二叉樹進一步細分(另外的文章再仔細研究)。

2. 霍夫曼樹：又稱為最優二叉樹，是一種帶權路徑最短的二叉樹。

3. B樹：是一種對讀寫操作進行優化的自平衡的二叉查找樹，能夠保持數據有序，擁有多余兩個子樹。

關于數據結構之樹的示例分析就分享到這里了，希望以上內容可以對大家有一定的幫助，可以學到更多知識。如果覺得文章不錯，可以把它分享出去讓更多的人看到。