C/C++經典算法之約瑟夫問題的示例分析

這篇文章給大家分享的是有關C/C++經典算法之約瑟夫問題的示例分析的內容。小編覺得挺實用的，因此分享給大家做個參考，一起跟隨小編過來看看吧。

什么是約瑟夫問題？ 

約瑟夫問題：n個人圍成一圈，初始編號從1~n排列，從約定編號為x的人開始報數，數到第m個人出圈，接著又從1開始報數，報到第m個數的人又退出圈，以此類推，最后圈內只剩下一個人，這個人就是贏家，求出贏家的編號。

是不是有點點復雜，其實該問題歸結為模擬類型的算法題，根據題目要求模擬即可。

我說，一行代碼解決約瑟夫問題！

？？？我去

別著急，我們一步一步學習

方法一：數組

在第一次遇到這個題的時候，我是用數組做的，我猜絕大多數人也都知道怎么做。方法是這樣的：

用一個數組來存放 1，2，3 ... n 這 n 個編號，如圖（這里我們假設n = 6, m = 3）

 然后不停著遍歷數組，對于被選中的編號，我們就做一個標記，例如編號 arr[2] = 3 被選中了，那么我們可以做一個標記，例如讓 arr[2] = -1，來表示 arr[2] 存放的編號已經出局的了。

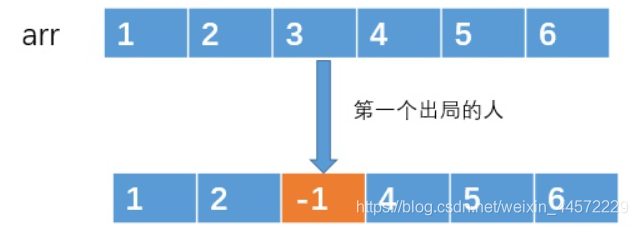
然后就按照這種方法，不停著遍歷數組，不停著做標記，直到數組中只有一個元素是非 -1 的，這樣，剩下的那個元素就是我們要找的元素了。我演示一下吧：

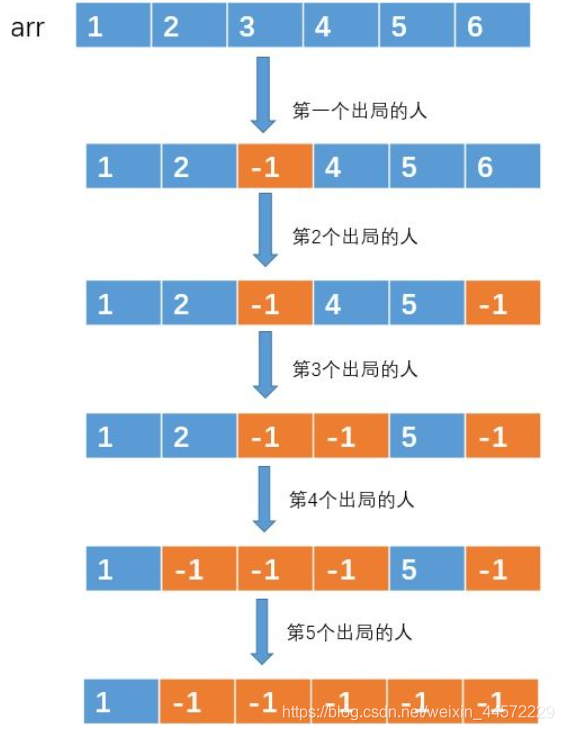
這種方法簡單嗎？思路簡單，但是編碼卻沒那么簡單，臨界條件特別多，每次遍歷到數組最后一個元素的時候，還得重新設置下標為 0，并且遍歷的時候還得判斷該元素時候是否是 -1。用這種數組的方式做，千萬不要覺得很簡單，編碼這個過程還是挺考驗人的。

這種做法的時間復雜度是 O(n * m), 空間復雜度是 O(n);

下面給出數組方法的參考代碼：

#include<algorithm>
#include<iostream>
using namespace std;
int main(){
	int a[1001]={0}; //初始化化數組作為環
	int n,m;//n代表總的人數，m代表報數到幾退出
	cin>>n>>m;
	int count=0;//記錄退出的個數
	int k=-1;//這里假定開始為第一個人，下標為0，編號為1，如需從編號x開始，則k=x-2
	while(count<n-1){  //總共需要退出n-1個人
		int i=0;//記錄當前報數編號
		while(i<m){
			k=(k+1)%n; //循環處理下標
			if(a[k]==0){
				i++;
				if(i==m){
					a[k]=-1;
					count++;
				}
			}
		}
	}
	for(int i=0;i<n;i++){
		if(a[i]==0){
			printf("%d\n",i+1);
			break;
		}
	}
	return 0;
}

方法二：環形鏈表

學過鏈表的人，估計都會用鏈表來處理約瑟夫環問題，用鏈表來處理其實和上面處理的思路差不多，只是用鏈表來處理的時候，對于被選中的編號，不再是做標記，而是直接移除，因為從鏈表移除一個元素的時間復雜度很低，為 O(1)。當然，上面數組的方法你也可以采用移除的方式，不過數組移除的時間復雜度為 O(n)。所以采用鏈表的解決方法如下：

1、先創建一個環形鏈表來存放元素：

2、然后一邊遍歷鏈表一遍刪除，直到鏈表只剩下一個節點，我這里就不全部演示了

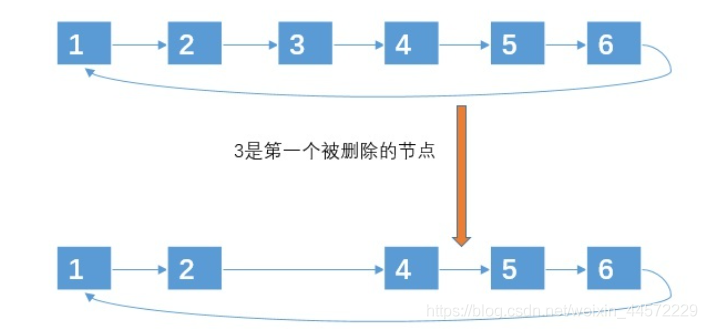
感興趣的友友可以自己實現以下代碼，這里就不放了

下面我們來看看，是如何一行代碼實現約瑟夫問題！

方法三：遞歸

其實這道題還可以用遞歸來解決，遞歸是思路是每次我們刪除了某一個人之后，我們就對這些人重新編號，然后我們的難點就是找出刪除前和刪除后編號的映射關系。

我們定義遞歸函數 f(n，m) 的返回結果是存活士兵的編號，顯然當 n = 1 時，f(n, m) = 1。假如我們能夠找出 f(n，m) 和 f(n-1，m) 之間的關系的話，我們就可以用遞歸的方式來解決了。我們假設人員數為 n, 報數到 m 的人就自殺。則剛開始的編號為

… 1 ... m - 2

m - 1

m

m + 1

m + 2 ... n …

進行了一次刪除之后，刪除了編號為 m 的節點。刪除之后，就只剩下 n - 1 個節點了，刪除前和刪除之后的編號轉換關系為：

刪除前 --- 刪除后

… --- …

m - 2 --- n - 2

m - 1 --- n - 1

m ---- 無(因為編號被刪除了)

m + 1 --- 1(因為下次就從這里報數了)

m + 2 ---- 2

… ---- …

新的環中只有 n - 1 個節點。且刪除前編號為 m + 1, m + 2, m + 3 的節點成了刪除后編號為 1， 2， 3 的節點。

假設 old 為刪除之前的節點編號， new 為刪除了一個節點之后的編號，則 old 與 new 之間的關系為 old = (new + m - 1) % n + 1。

 注：有些人可能會疑惑為什么不是 old = (new + m ) % n 呢？主要是因為編號是從 1 開始的，而不是從 0 開始的。如果 new + m == n的話，會導致最后的計算結果為 old = 0。所以 old = (new + m - 1) % n + 1. 這樣，我們就得出 f(n, m) 與 f(n - 1, m)之間的關系了，而 f(1, m) = 1.所以我們可以采用遞歸的方式來做。

 代碼如下：

int f(int n, int m){
    return n == 1 ? n : (f(n - 1, m) + m - 1) % n + 1;
}

感謝各位的閱讀！關于“C/C++經典算法之約瑟夫問題的示例分析”這篇文章就分享到這里了，希望以上內容可以對大家有一定的幫助，讓大家可以學到更多知識，如果覺得文章不錯，可以把它分享出去讓更多的人看到吧！