您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“PHP怎么使用動態規劃實現最優紅包組合”,在日常操作中,相信很多人在PHP怎么使用動態規劃實現最優紅包組合問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”PHP怎么使用動態規劃實現最優紅包組合”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
動態規劃 (Dynamic programming 簡寫:DP)是一種在數學、管理科學、計算機科學、經濟學和生物信息學中使用的,通過把原問題分解為相對簡單的子問題的方式求解復雜問題的方法。
動態規劃常常適用于有重疊子問題和最優子結構性質的問題,動態規劃方法所耗時間往往遠少于樸素解法。
一般使用動態規劃來解決求最優解的問題。在解決問題的過程中需要多次決策,而每次決策都有產生一組狀態,然后從最優的決策中繼續下一次的決策,最終找到最優的結果。
另外動態規劃還具有3個特征,如下:
如果問題的最優解所包含的子問題的解也是最優的,我們就稱該問題具有最優子結構性質(即滿足最優化原理)。從而我們可以通過子問題的最優解,推導出問題的最優解,也可以理解為后面階段的狀態可以通過前面階段的狀態推導出來。
即子問題的解一旦確定,就不再改變,不受在這之后、包含它的更大的問題的求解決策影響。
可以簡單理解為 在推導后面階段狀態的時候,我們只需要關心它前一階段的狀態狀態,不用去關心這個狀態是怎么一步步推導出來的。第二個含義就是某個階段的狀態一旦確定下來,就不會受之后階段的決策影響。
子問題重疊性質是指在用遞歸算法自頂向下對問題進行求解時,每次產生的子問題并不總是新問題,有些子問題會被重復計算多次
上面的理論比較抽象,和扯犢子一樣的,來看下經典的背包問題。
假設現在有5個物品他們的重量分別是 2, 2, 5, 11, 4, 現在有一個背包,能承受的最大重量是 10,請選擇合適的物品放入背包,那么能組合出的物品最大重量是多少?
不同的物品組合會有多種不同的狀態,我們可以使用 f(i, w) 來表示一種狀態,其中 i = index 表示第幾個物品, w = weight 表示當前的總重量。
整個問題的求解需要經過 『n』 個階段,每個階段都需要決策一個物品是否放入背包,決策的結果只有2種 『放入』 或者 『不放入』。在決策完一個物品后,背包中的物品重量會有很多種不同的狀態,我們需要把每一層的 重復狀態 合并,然后只留下不同的狀態。然后基于上一層的狀態結果來推導出下一層的狀態結果。最終全部物品決策完就可以找到最優的組合解。
第0(其實也就是第一個物品,按照習慣從0開始下標吧)個物品的重量是2,然后開始決策是否放入背包,結果只有2種。如果放入背包那么此時背包的重量就是2,如果不放入背包那么背包的重量就是0.記作 $status[0][0] = true; 和 $status[0][2] = true; 和上面的 f(i, w) 一樣,前一位表示物品,后一位表示重量。
第1個物品的重量還是2,然后開始對他決策,決策只有2種選擇 放入背包 或者 不放入背包,但是它的狀態組合卻多了,因為它要基于之前的背包狀態來判斷當前的狀態。對第1個物品完成決策后會有3個狀態(其實是4個狀態,不過有1個重復的就不算了 還是算3個不同的狀態)。
如果決策當前物品放入背包,第0個物品不放入背包,此時的狀態是 $status[1][2 + 0] = true; => $status[1][2] = true;
如果決策當前物品放入背包,第0個物品也放入背包,此時的狀態是 $status[1][2 + 2] = true; => $status[1][4] = true;
如果決策當前物品不放入背包,第0個物品不放入背包,此時的狀態是 $status[1][0 + 0] = true; => $status[1][0] = true;
如果決策當前物品不放入背包,而第0個物品放入背包,此時的狀態是 $status[1][0 + 2] = true; => $status[1][2] = true;
其中 $status[1][2] 是重復的,所有會產生3種結果。
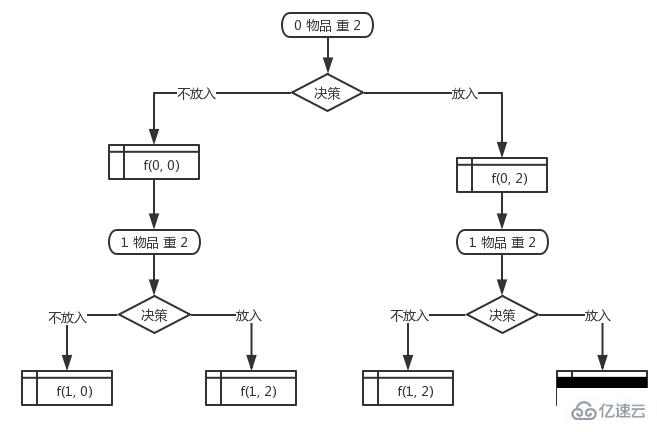
后面的物品也是以此類推,直到對所有的物品都決策完,整個狀態的數組就都找出來了,然后只需要在最后一層找到一個值為true的最接近最大值(上面的例子中是10)的值就是背包能承受的最大值。然后可以從最后依次往前推就可以找出對應的物品下標,也就是哪些物品的組合是這個最優解組合了。
推導過程如下圖:



實際上在上面的推導過程中就是動態規劃的解題思路。把問題分解為多個階段,每個階段對應一種策略。然后記錄下每個階段的狀態(注意要去掉重復項),然后通過當前狀態的可能推導出下一個階段的所有狀態可能,動態的推導下去。
PHP實現偽代碼:
function dynamicKnapsack($arr, $n, $max){
// 初始化二維數組
$status = [];
for ($i = 0; $i < $n; $i++) {
// max + 1 才能有max的值 因為下標從0開始的
for ($j = 0; $j < $max + 1; $j++) {
$status[$i][$j] = 0;
}
}
// 第一個物品特殊處理
// 對第一個物品決策不放入
$status[0][0] = 1;
// 對第一個物品決策放入
if ($arr[0] <= $max) {
$status[0][$arr[0]] = 1;
}
// 開始動態規劃進行決策 -- 外層是物品
for ($i = 1; $i < $n; $i++) {
// 決策放入背包
for ($j = 0; $j < $max + 1; $j++) {
// 找到他上一層的組合,在上一層的基礎上變更當前層的結果
if ($status[$i - 1][$j] == 1) {
$status[$i][$j + $arr[$i]] = 1;
}
}
// 決策不放入背包
for ($j = 0; $j < $max + 1; $j++) {
// 找到上一層的組合直接取上一層的值
if ($status[$i - 1][$j] == 1) {
// $status[$i][$j] = 1; 等價于下面
$status[$i][$j] = $status[$i - 1][$j];
}
}
}
// 尋找最優組合
$best = [];
$j = 0;
// 為了找到尋找最優解的開始位置
// 也就是當前能組合出的最大值是多少
// 最后一行是最大的組合,它包含了所有都放入的結果
// 最終確定了j開始的位置
for ($j = $max; $j >= 0; $j--) {
if ($status[$n - 1][$j] == true) {
break;
}
}
for ($i = $n - 1; $i >= 1; $i--) { // 外層遍歷行
if ($j - $arr[$i] >= 0 && $status[$i - 1][$j - $arr[$i]] == 1) {
var_dump('buy this product: '.$arr[$i]);
$best[] = $i;
$j = $j - $arr[$i];
}
}
if ($j != 0) {
var_dump('buy first product:'.$arr[0]);
$best[] = 0;
}
return $best;}// 測試數據$arr = [
2, 2, 5, 11, 4,];$n = 5;$max = 10;$best = dynamicKnapsack($arr, $n, $max);var_dump($best);如果求的結果是 11,得出的結果是 4, 5, 2 的組合,你可能會有疑問不是還有11這個結果么,剛好它一個就滿足了不是么。我覺得這個應該是看實際的需求。比如我這次的需求是把紅包按過期時間排序,快過期的優先使用,然后我在組裝數據的時候按過期時間順序強行把快過期的紅包放到數組最后面拼成數組,那最后的4就是最接近快過期的紅包了,我要優先消耗掉這個紅包,如果使用了4那11就不能使用了,只能繼續去前面找,就是這么回事!
這段代碼的時間復雜度是多少? 耗時最多的部分是中間的嵌套2層循環,所有時間復雜度是 O(n*max),其中 n 表示物品的個數,max表示最大的承重。
空間復雜度是一開始申請的數組空間 O(n*max+1) 加上計算結果的累加有可能出現 O(n*2*max) 的情況,空間消耗還是很高的。
總體來說這是一種空間換時間的思路。另外在中間決策的嵌套循環里如果使用j從小到大遍歷的話會出現for循環重復計算的問題。
到此,關于“PHP怎么使用動態規劃實現最優紅包組合”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。