您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要講解了“怎么用C++實現搭積木小游戲”,文中的講解內容簡單清晰,易于學習與理解,下面請大家跟著小編的思路慢慢深入,一起來研究和學習“怎么用C++實現搭積木小游戲”吧!
小明對搭積木非常感興趣。他的積木都是同樣大小的正立方體。
在搭積木時,小明選取 m 塊積木作為地基,將他們在桌子上一字排開,中間不留空隙,并稱其為第0層。
隨后,小明可以在上面擺放第1層,第2層,……,最多擺放至第n層。擺放積木必須遵循三條規則
規則1:每塊積木必須緊挨著放置在某一塊積木的正上方,與其下一層的積木對齊;
規則2:同一層中的積木必須連續擺放,中間不能留有空隙;
規則3:小明不喜歡的位置不能放置積木。
其中,小明不喜歡的位置都被標在了圖紙上。圖紙共有n行,從下至上的每一行分別對應積木的第1層至第n層。每一行都有m個字符,字符可能是‘.'或‘X',其中‘X'表示這個位置是小明不喜歡的。
現在,小明想要知道,共有多少種放置積木的方案。他找到了參加藍橋杯的你來幫他計算這個答案。
由于這個答案可能很大,你只需要回答這個答案對1000000007(十億零七)取模后的結果。
注意:地基上什么都不放,也算作是方案之一種。
輸入格式:
數據的第一行有兩個正整數n和m,表示圖紙的大小。
隨后n行,每行有m個字符,用來描述圖紙 。每個字符只可能是‘.'或‘X'。
輸出格式:
一個整數,表示答案對1000000007取模后的結果。
輸入樣例1:
2 3
..X
.X.
輸出樣例1:
4
輸入樣例2:
3 3
..X
.X.
...
輸出樣例2:
16
解題思路:
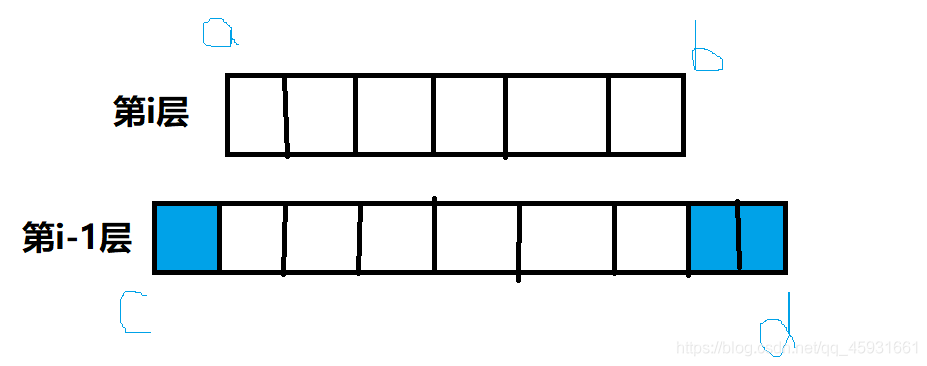
首先先推導出遞推式,觀察題目,可以得到遞推式為:
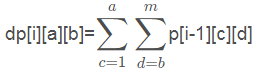
用代碼表示即為:
for(int c=1;c<a;c++){
for(int d=b;d<m;d++){
dp[i][a][b]+=dp[i-1][c][d];
}
}意思是
在第i層的a到b長度放置積木的可能數=在i-1層的所有包含a到b的長度的積木的可能數的和。
除了單純的判斷遞推式以外,還需要考慮一種特殊情況,就是積木放置的長度中存在X,即小明不想放的位置,那么就不需要進行遞推,直接返回0。
判斷[a,b]是否存在X,可以用前綴和來判斷,節省時間。
前綴和初始化為:
s[i][j] = s[i][j-1] + (temp=='X');
推導出遞推式以后可以很容易的寫出代碼:
#include<iostream>
using namespace std;
const int N = 30;
int n, m;
int dp[30][30][30];
int s[30][30];
int cnt=1;
int main() {
cin >> n >> m;
getchar();
for (int i = n; i >0; i--) {//初始化前綴和
for (int j = 1; j <= m; j++) {
char temp = getchar();
s[i][j] = s[i][j-1] + (temp=='X');
}
getchar();
}
dp[0][1][m]=1;//第0層,長度從1到m的積木有一種可能
for (int i = 1; i <=n; i++) {//第i層
for (int a = 1; a <= m; a++) {
for (int b = a; b <= m; b++) {
if (s[i][b] - s[i][a - 1] != 0) {//a到b區間存在X
dp[i][a][b] = 0;
continue;
}
for (int c = 1; c <= a; c++) {
for (int d = b; d <= m; d++) {
dp[i][a][b] += dp[i - 1][c][d];
}
}
cnt += dp[i][a][b];//記錄數量
}
}
}
cout << cnt;
return 0;
}優化
但是仔細一想,五個for循環無法通過最后50%的測試點,所以需要進行優化,觀察最內層的兩個c,d的for循環可知,有如下圖像:
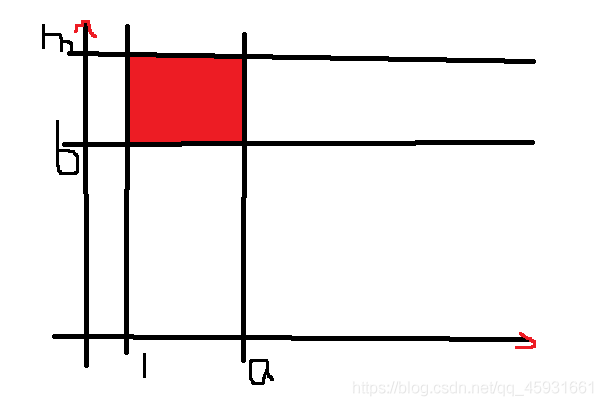
實際上最內層的兩個循環就是在求第i-1層的紅色區域面積。
那我們再利用二維的前綴和進行存儲,那就可以優化掉兩個循環,從而使時間復雜度降低,通過最后的測試點。
#include<iostream>
using namespace std;
const int N = 30;
const int mod = 1e9 + 7;
int n, m;
int dp[30][30][30];
int s[30][30];//用來判斷是否存在X
int sum[30][30];//指的是左下角所有dp[i][][]的和
int cnt=1;
void get_fixsum(int i) {
//更新第i層的前綴和數組
for (int a = 1; a <= m; a++) {
for (int b = 1; b <= m; b++) {
sum[a][b] =(sum[a][b-1]+sum[a-1][b]-sum[a-1][b-1]+ dp[i][a][b])%mod;
}
}
}
int main() {
cin >> n >> m;
getchar();
for (int i = n; i >0; i--) {
for (int j = 1; j <= m; j++) {
char temp = getchar();
s[i][j] = s[i][j-1] + (temp=='X');
}
getchar();
}
dp[0][1][m]=1;//第0層,長度從1到m的積木有一種可能
get_fixsum(0);
for (int i = 1; i <=n; i++) {//層數
for (int a = 1; a <= m; a++) {
for (int b = a; b <= m; b++) {
if (s[i][b] - s[i][a - 1] != 0) {//a到b區間存在X
dp[i][a][b] = 0;
continue;
}
dp[i][a][b] = (sum[a][m] - sum[0][m] - sum[a][b-1] + sum[0][b-1])%mod;
cnt =(cnt+ dp[i][a][b])%mod;
}
}
get_fixsum(i);
}
cout << (cnt+mod)%mod;//防止出現負數
return 0;
}感謝各位的閱讀,以上就是“怎么用C++實現搭積木小游戲”的內容了,經過本文的學習后,相信大家對怎么用C++實現搭積木小游戲這一問題有了更深刻的體會,具體使用情況還需要大家實踐驗證。這里是億速云,小編將為大家推送更多相關知識點的文章,歡迎關注!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。