您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章將為大家詳細講解有關Cochran-Mantel-Haenszel檢驗在關聯分析中的應用是怎樣的,文章內容質量較高,因此小編分享給大家做個參考,希望大家閱讀完這篇文章后對相關知識有一定的了解。
Cochran-Mantel-Haenszel, 簡稱CMH檢驗,是分析兩個二分類變量之間關聯性的一種檢驗方法,在2 x 2 表格數據的基礎上,引入了第三個分類變量,稱之為混雜變量。混雜變量的引入使得該檢驗可以用于分析分層樣本,作為生物統計學領域的一種常用技術,該檢驗常用于疾病對照研究。
下面來看一個最基本的例子,研究不同性別和候選人投票結果之間的關聯,得到如下所示的2 x 2的表格
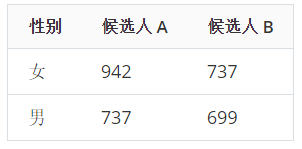
這里有兩個二分類變量,第一個是投票者的性別,第二個是候選人A和B。考慮到所有的投票者本身存在分層現象,來自3個不同的州,針對不同的州重新統計,得到如下的結果
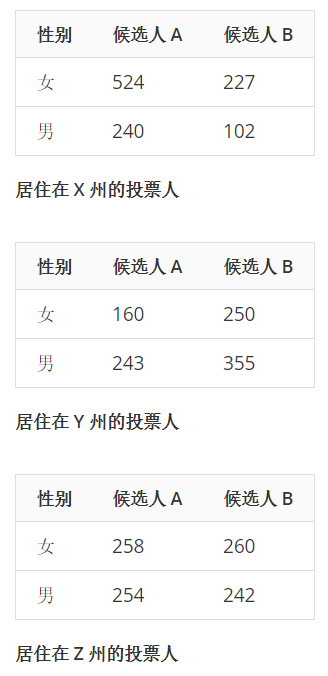
上述例子中,投票者出現了分層現象,來自3個不同的州。如果不考慮這個因素,直接統計性別和候選人的頻數分布,采用卡方或者費舍爾精確檢驗來進行分析,即使得到了陽性的結果,也無法確定是不同性別之間真實存在投票的差異還是由于來自不同的州導致了這樣的差異。
由于投票者的分層現象,直接采用卡方或者費舍爾精確檢驗進行分析是不太合適的。在上述模型中,投票者的分層就是一個典型的混雜變量,對于這樣的數據可以采用CMH檢驗進行分析。
CMH檢驗針對每個分層統計2X2的表格,計算每一層的odd ratio值,然后在進行加權,計算公共的odd ratio, 每一層用i表示,統計的2X2表格數據如下
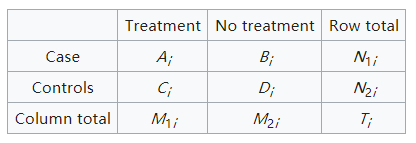
common odd raio的計算公式如下
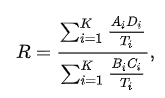
從公式可以看出,利用每層的樣本總數進行了加權,用于CMH分析的數據要求樣本量比較大,以保證每層的頻數表格中不會出現0的情況。該檢驗的統計量公式如下
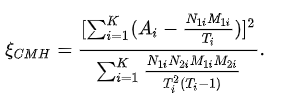
服從自由度為1的卡方分布,上述數據在R中進行CMH檢驗的代碼如下
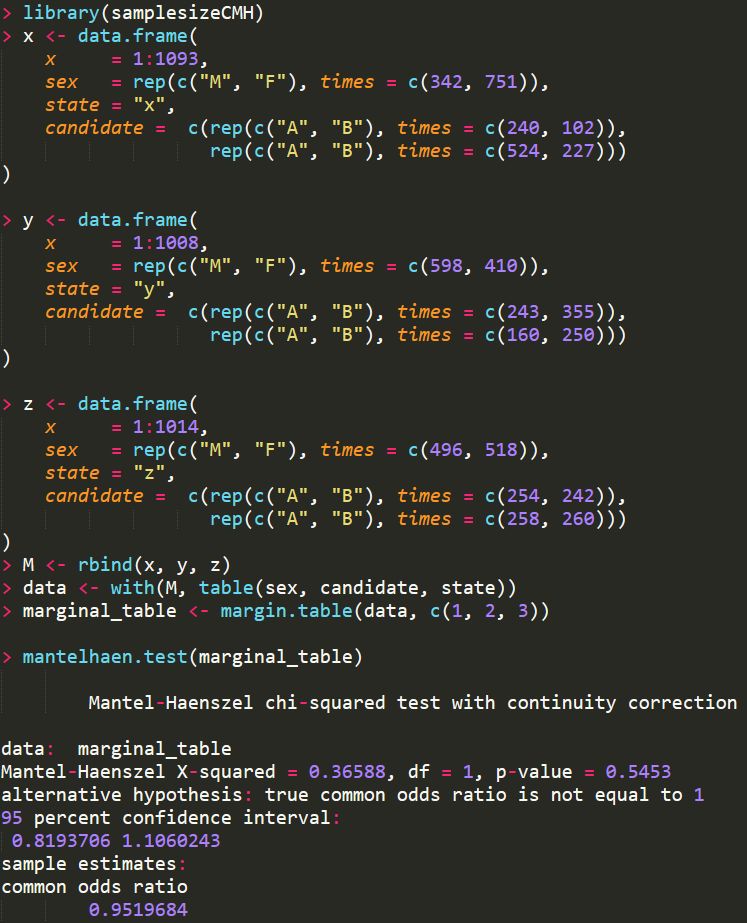
pvalue值大于0.05. 說明性別和候選者之間沒有關聯。如果直接對總體結果進行卡方或者費舍爾精確檢驗的話,得到的結論相反,計算過程如下
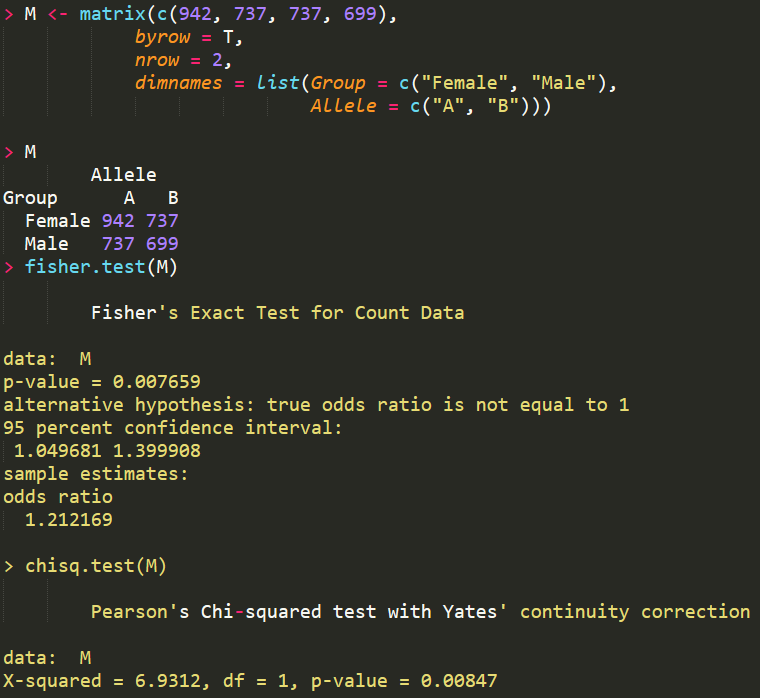
從這個數據可以看出,對于分層樣本,有必要進行CMH檢驗。需要說明的是,CMH檢驗假設所有分層的odd raio值相同,可以通過Breslow-Day test來進行檢驗,代碼如下
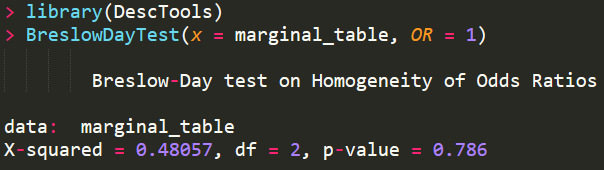
pvalue值大于0.05,說明不滿足odd ratio齊性。當然對于分層數據,除了CMH檢驗外,邏輯回歸也是一個很好的解決方法,而且更加通用,可以將混雜變量當做回歸分析中的協變量來進行處理。
關于Cochran-Mantel-Haenszel檢驗在關聯分析中的應用是怎樣的就分享到這里了,希望以上內容可以對大家有一定的幫助,可以學到更多知識。如果覺得文章不錯,可以把它分享出去讓更多的人看到。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。