您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要講解了“非層次聚類中clusplot()函數怎么用”,文中的講解內容簡單清晰,易于學習與理解,下面請大家跟著小編的思路慢慢深入,一起來研究和學習“非層次聚類中clusplot()函數怎么用”吧!
k-means算法中選取的是距離均值,那么異常點對其的影響會非常大,很可能這種孤立的點就聚為一類,一個改進的方法就是圍繞實際數據的中心點進行劃分(partitioning aroundmedoids,PAM),也叫k-medoids clustering。其與k-means算法類似,從所有數據觀測點尋找k個代表性的對象或形心點,來反應數據的主體結構,然后將所有觀測點分配給每個形心點構建k個分類簇。不斷迭代來尋找k個代表對象,來獲得最佳的形心點來使得對象間的相異性總和最小。
k-medoids算法是k-means算法的變種,其不一樣的地方在于聚類中心的選取。在k-means算法中將聚類中心選取為當前cluster中所有數據點的平均值,也即非真實的數據點;然而k-medoids算法中,將聚類中心也即中心點的選取限制在當前cluster所包含的數據點的集合中,從當前cluster中選取到其他所有點的距離之和最小的點作為中心點。k-means和k-medoids之間的差異就類似于一個數據樣本的均值和中位數之間的差異。
cluster包中的pam()函數可以使用原始數據或者距離矩陣進行分析,因此十分方便,還可以通過輪廓寬度值確定最佳的分組數量,而fpc包中的pamk()函數可以自動計算最佳的分類簇數目,實例分析如下所示:
#讀取數據data=read.table(file="otu_table.txt", header=TRUE, check.names=FALSE)rownames(data)=data[, 1]data=as.matrix(data[, -1])#將每個樣品的物種數據進行總和標準化(即求相對豐度)library(vegan)data=decostand(data, MARGIN=2, "total")*100otu=t(data)#計算距離矩陣otu_dist=vegdist(otu, method="bray", diag=TRUE, upper=TRUE, p=2)#PAM聚類library(fpc)library(cluster)#確定最佳聚類簇數目pambest=pamk(otu_dist)k=pambest$ncotu_pam=pam(otu_dist, k)mycol=c(99,81,503,562,76,96,495,52,619,453,71,134,448,548,655,574,36,544,89,120,131,596,147,576,58,429,386,122,87,404,466,124,463,552,147,45,30,54,84,256,100,652,31,610,477,150,50,588,621)mycol=colors()[mycol]clusplot(otu_pam, color=TRUE, labels=3, lines=0, cex=1, col.clus=mycol[1:k], col.p=otu_pam$clustering)
clusplot()函數可以對聚類結果進行主成分分析并作圖,結果如下所示:

根據pamk()函數計算結果最佳聚類簇數目為10,但主成分聚類圖顯示的聚類簇數目要小于10,可以看到不同算法的差異。我們也可以針對PAM聚類繪制輪廓寬度圖,從而幫助挑選最佳聚類簇數目,如下所示:
#繪制輪廓寬度圖asw=numeric(nrow(otu))for (i in 2:(length(asw)-1)) { asw[i]=pam(otu_dist, i)$silinfo$avg.width}k.best=which.max(asw)plot(1:length(asw), asw, type="h", main="Silhouette of PAM", lwd=2, xlab="k(number of clusters", ylab="average silhouette")
結果如下所示:
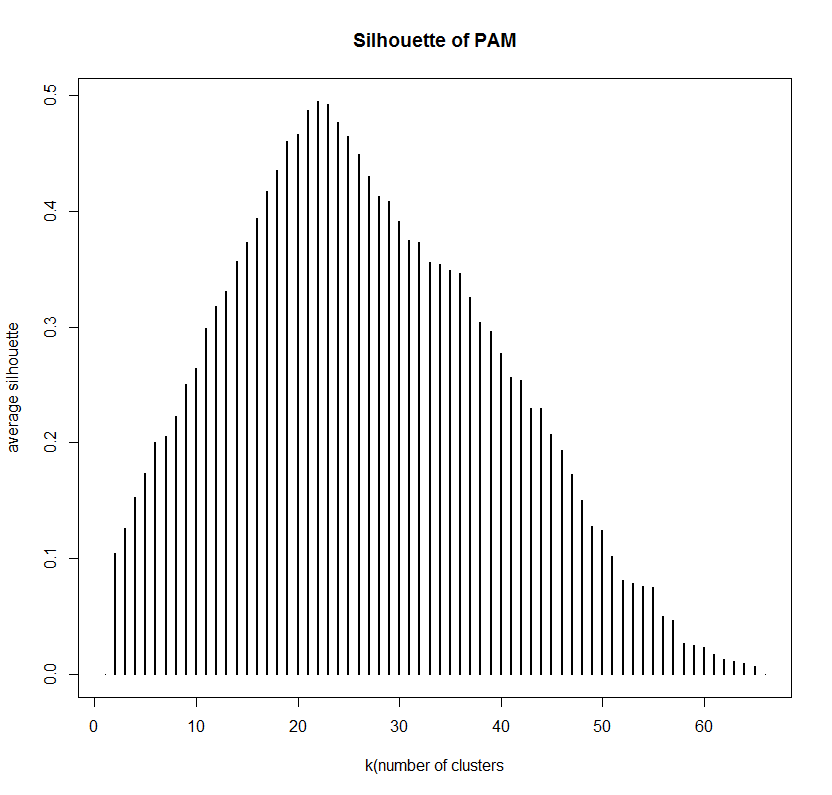
當k=22時取得最高的輪廓寬度,這與事實是相符的,因為我們所用數據的66個樣品采自22個樣品點,每個點3個平行樣。但總體來看,輪廓寬度值很高,因此不一定挑選k=22,這里只是為pamk()函數判斷結果作參考。
感謝各位的閱讀,以上就是“非層次聚類中clusplot()函數怎么用”的內容了,經過本文的學習后,相信大家對非層次聚類中clusplot()函數怎么用這一問題有了更深刻的體會,具體使用情況還需要大家實踐驗證。這里是億速云,小編將為大家推送更多相關知識點的文章,歡迎關注!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。