如何處理報表中的舍位平衡

在報表的數據統計中，常常會根據精度呈現或者單位換算等要求，需要對數據執行四舍五入的操作，這種操作稱為舍位處理。簡單直接的舍位處理有可能會帶來隱患，原本平衡的數據關系可能會被打破。

為了保證報表中數據關系的正確，就需要調整舍位之后的數據，使得數據重新變得平衡，這樣的調整就叫做舍位平衡。在這里我們就討論一下如何利用集算器來處理舍位平衡問題。

舍位處理往往會采取四舍五入計算，這時就會產生誤差，而如果報表中有這些數據的合計數值，那么舍位時產生的誤差就會積累，有可能導致舍位過的數據與其合計值無法匹配。例如，保留一位小數的原始的數據是4.5+4.5=9.0，而四舍五入只保留整數部分后，平衡關系就變為5+5=9了，看上去明顯是荒謬的。在這樣的情況下，需要在保持合計值正確的條件下，調整非合計數據舍位后的結果，使得數據關系重新平衡，例如調整為4+5=9。這個簡單的例子就是典型舍位平衡。

1. 單向舍位平衡

如果在數據統計時，每個數據只用于一次合計，那么在處理舍位平衡時，只需要根據合計值的誤差，調整使用的各項數據就可以了，這屬于比較簡單的情況。例如：

A1的序列中存儲了一些數據,在B1中計算了它們的合計值，結果如下：

現在，將數據取整，重新統計。A2中將序列中每個數據用round函數四舍五入取整，得到新的序列。在B2中則將B1中的結果取整，這是數據取整后應該獲得的結果。在C2中則只是簡單地用取整后的數據來求和。A2，B2和C2中結果分別如下：

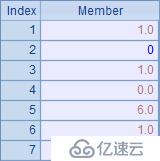
顯然，舍位后誤差的累積導致數據不再平衡，將原始數據分別四舍五入后，總和由12變成了10。那么，能不能把合計數直接改為10呢？這是不行的，因為這樣會使得最終結果與真實值完全不符。因此，為了保證舍位后仍然能夠保持平衡關系，應該分別改變各個原始數據舍位后的結果。

舍位后總計產生的誤差，稱為“平衡差”，舍位平衡其實就是消除平衡差的過程。處理舍位平衡的規則有很多，下面我們分別進行研究：

(1) 將平衡差整理到第一個數據中。即：

B2中，把平衡差折算到舍位后的第一個數據中。整理后，在C2中重新計算了舍位平衡處理后的合計值。A2和C2中的結果如下：

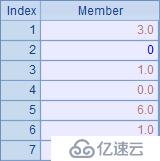
這種舍位平衡的處理規則最為簡單。但是，舍位后第1個數據由1.48變為了3，明顯偏移了很多，因此這樣的處理不夠合理，特別是在數據很多的情況下，平衡差也有可能會累積的很大，進而致使第1個數據產生非常荒謬的偏移結果。

(2) 將平衡差按照“最小調整值”，對絕對值比較大的數據進行分擔調整。

所謂最小調整值，就是舍位后最小精度的單位值，例如在取整時，最小精度就是個位，最小調整值就是1或者-1。如果舍位后合計值變小，則需要將數據調大，那么最小調整值就是1；如果舍位后合計值變大，則需要將數據調小，最小調整值就是-1。而調整只針對絕對值比較大的數據，這樣它們的相對偏差就會比較小。具體調整幾個數，那就是合計值偏差除以最小調整值。

在這種規則下，前面問題的舍位平衡處理如下：

因為只是取整操作，因此C2中計算的最小調整值就是合計值偏差的正負；

A3中，根據原始數據的絕對值從大到小做了一個排序，結果就是排序后的序號。

B3是最主要的，因為只是取整操作，所以B2中的偏差絕對值是多少，就調整幾個數。以此循環，依照原始值的絕對值大小，依次分配最小調整值。

C3是對調整后的A2重新驗證了合計值。

調整后，A2和C3中的結果如下：

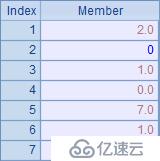
在這種方案中，平衡差由多個數據分擔，而選擇絕對值最大的數據會使得數據的相對變動最小。在結果中，1.48舍位后變為了2，6.48舍位后變為了7，調整平衡的結果還是比較理想的。

這種方案需要將數據按絕對值排序，執行效率不是很好，特別是在數據量比較大的情況下，排序會耗費較多時間。

(3) 將平衡差按照最小調整值，由不為0的數據依次分擔。

在上一種調整舍位平衡的方案中，將誤差由絕對值最大的一些數據來分擔。在實際操作中，為了提高效率，減少排序操作，就可以適當簡化，改為由順序排在前幾位的數據來分擔。考慮到在四舍五入時，0并不會產生誤差，而且如果修改數據中的0，這樣的變動會比較明顯，因此在調整時將保留原始數據中的0不變。

在這種規則下，前面問題的舍位平衡處理如下：

A3中選擇出原始數據中非0成員的序號，在B3中調整舍位后數據時，按順序分擔。調整后，A2和C3中的結果如下：

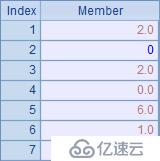
在結果中，1.48舍位后變為了2，1.42舍位后變為了2，調整平衡的結果比較合理。同時這種方案避免了排序操作，效率較高，因此這種舍位平衡的規則最為常用。

在處理單向舍位平衡時，并非只有對一組序列求和的情況。更多的情況下，是對一批數據來求和，如下面的SalesRecord.txt中存儲的序表：

現在，需要統計每位員工4個月的總銷售額，統計時以千元為單位，并處理舍位平衡。代碼如下：

分步執行代碼，A1中讀入序表后，在B1中添加合計字段Sum，結果如下：

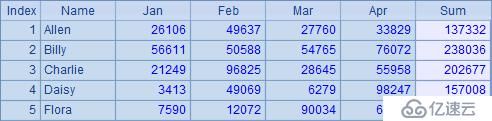
在C1中將上面的序表復制，并在B1中將序表中的第2至第6個字段執行舍位計算到以千為單位。此時，有可能由于四舍五入計算破壞平衡，在B2中再添加一個字段Sum2，計算舍位后4個月的合計值。B2中的序表如下：

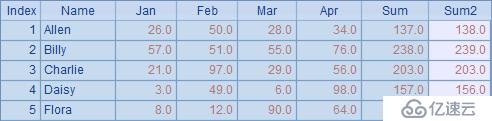
可以看到，在此時，Sum與Sum2字段是有區別的，說明需要調整舍位平衡。在這里雖然需要調整計算后序表中的數據，但是每個數據只用于計算員工合計，因此仍然屬于單向舍位平衡。

A5中的子程序用來處理一條記錄的舍位平衡，B5中計算平衡差，C5中計算出最小調整值。在B6中循環，將平衡差拆分到記錄中前幾個數據中，這里簡單處理，并未判斷數據是否非零。

在A3中，循環序表B2中的記錄，分別調整舍位平衡。調整完畢后，在A4中再添加Sum3字段來驗證舍位平衡結果，A4中結果如下：

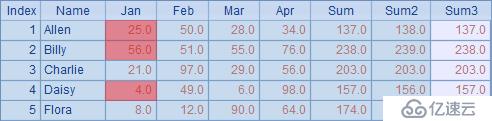
對比Sum與Sum3可以確認，結果調整，數據舍位后重新達成了平衡。

2. 雙向舍位平衡

如果數據在行向和列向兩個方向同時需要計算合計值，同時還需要計算所有數據的總計值，這種情況下處理舍位平衡時就復雜得多了。此時處理舍位平衡時，不僅要求最終的總計值準確，同時行向和列向計算的合計值也要與對應行、列的數據平衡，這種情況下的舍位平衡稱為雙向舍位平衡。如在SalesRecord.txt的數據中，需要再統計每個月的總銷售額，代碼如下：

A1中讀入序表，并在B1中添加一條記錄，用來在D1中計算各月總銷售額。再在A2中添加字段計算每位員工的銷售總額，以及總合計值后，結果如下：

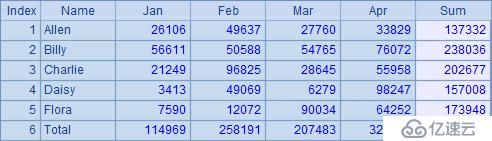
在C2中根據上面的匯總數據，將結果舍位到以千元為單位。再根據舍位后的數據，在A3中添加字段Sum2計算舍位后的員工合計值，在B3中添加字段Diff員工合計的平衡差。最后，再添加2條記錄，分別用來計算每個月的舍位合計值，以及平衡差。計算完成后，B3中結果如下：

可以看到，當橫向和縱向分別做匯總時，舍位后需要解決的平衡問題就復雜得多了。此時修改任何一個舍位數據，都會同時影響橫向和縱向兩個方向的合計計算，這樣的問題稱為雙向舍位平衡。在上面的計算中，有一些平衡差只與合計值相關，如Total這一行中最右側的平衡差，只與各月的合計有關，這樣的平衡差稱為合計平衡差。在雙向舍位平衡表中，只存在一橫一縱兩個合計平衡差。其它的平衡差都會和具體數據相關，如Feb這個月最下方的平衡差，這種平衡差稱為非合計平衡差。

我們先從一些比較簡單的情況開始研究雙向舍位平衡：

(1)橫向與縱向的非合計平衡差符號相同。如下面的情況：

上面的表格中，存儲著2行2列的初始數據，同時計算出了各行各列的合計值，以及所有數據的總計值。下面將這些數據四舍五入取整，并計算每一行/列的平衡差，結果如下：

這里的“非合計平衡差”是指涉及原始數據的平衡差，此時合計數據及總計值都不需要調整。可以看到，此時只是第1行和第1列的合計值不平衡，而且都是合計值比舍位數據的和大1，這種情況下，只需要調整交叉點處的數據，根據平衡差符號加減最小調整值即可。具體操作是把交叉點處，即第1行第1列的數據舍位結果+1，就可獲得平衡，結果如下：

(2)同向的2個非合計平衡差符號相反。如下面的情況：

將這些數據四舍五入取整，并計算每一行/列的平衡差，結果如下：

這種情況下，仍然不需要調整總計值。由于第1列和第2列中的平衡差一正一負，只需要任選一行平衡差為0的數據，將這兩列的數分別根據按平衡差的符號加減最小調整值。如選擇第1行，將第1列的舍位結果+1，將第2列的舍位結果-1，就可獲得平衡，結果如下：

(3)某個合計平衡差與另一方向的非合計平衡差符號相反。如下面的情況：

將這些數據四舍五入取整，并計算每一行/列的平衡差，結果如下：

這種情況下，說明交叉點處的合計數據需要調整，只需要調整交叉點處的合計數據，根據合計平衡差的符號加減最小調整值。在這里，即修改第1列的合計結果，根據橫向的合計平衡差，將其-1，即可獲得平衡，結果如下：

(4)某個合計平衡差與同方向的非合計平衡差符號相同。如下面的情況：

將這些數據四舍五入取整，并計算每一行/列的平衡差，結果如下：

在這里是列向的合計平衡差與另一列的平衡差符號相同，在這種情況下，可以任選1行平衡差為0的數據，同時調整這2列的數據。如果選擇第1行，即同時調整第1行第1列，以及第1行的合計值，將它們分別+1即可獲得平衡，結果如下：

(5)兩個方向合計平衡差的符號相同。如下面的情況：

將這些數據四舍五入取整，并計算每一行/列的平衡差，結果如下：

此時，只有合計數據影響了結果的平衡。在這種情況下，可以任選一個非合計值，根據合計平衡差的符號加減最小調整值，同樣調整這個數據的橫向和縱向合計值。在上面例子中，可以任意選擇1個數據，如第2行第2列的值，根據平衡差將它+1，同時將第2行以及第2列的合計值同時都+1，這樣就可以獲得平衡，如下：

由于是任選數據，也有其它的處理方式，如選擇第1行第2列的數據修改，同樣可以獲得平衡，結果如下：

在處理雙向舍位平衡時，只有上面的5種情況可以調整平衡。對于其它的情況，說明計算有誤，是無法通過1次調整達成舍位平衡的。但是在實際處理中，上面的情況往往是混合出現的。因此，可以先處理第(1)種情況，即所有非合計行列平衡差符號相同的情況，再處理第(2)種情況，將非合計行/列中不同符號的平衡差消除。全部調整理完畢后，非合計行與非合計列的平衡差只能各為一種符號。此時再處理第(3)種和第(4)種情況，將非合計行/列的平衡差與合計行/列的平衡差配合消除。最后，如果兩個方向行/列的平衡差仍未消除，再按照第(5)中情況處理。這樣，就可以對一般性的表格完成雙向舍位平衡處理了。

再回到這一節開始時的銷售數據表，下面的代碼將處理其中的舍位平衡：

程序比較復雜，下面簡要說明一下功能。A26處的子程序用來修改序表中的1條記錄，將其指定位置的數據加上所需的調整值。由于用于計算的序表中，第一列為Name，實際并不參與計算，因此整理數據時將其跳過。C5和D5中分別獲得橫向和縱向的平衡差序列。在第6、7行，循環處理第(1)種情況，如果兩個方向的平衡差符號相同，改變交叉點處的舍位結果。在第8~13行，分橫縱兩種情況，處理第(2)種情況，如果同向的兩個平衡差符號相反時，修改這兩行/列中的舍位結果。第14~17行，處理第(3)種情況，當合計平衡差與另一方向的非合計平衡差符號相反時，調整交叉點處的合計結果。在第18~23行，處理第(4)種情況，當合計平衡差與同方向的非合計平衡差符號相同時，修改這兩行/列中的數據。最后，在第24和25行，判斷前面的修改完成后，是否仍然存在兩個合計平衡差，此時相應調整第1個數據的舍位結果，同時調整第1行和第1列的合計值。

雙向舍位平衡處理完成后，在B2中可以查看最終結果：

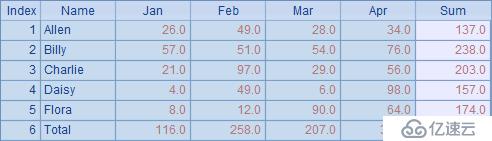
運算時，處理過程如下：

執行第(1)步處理，將不同方向上符號相同的非合計平衡差消除后，結果如下：

這個例子中，執行第(1)步處理后，并沒有符號相反的非合計平衡差，不需執行第(2)步處理。在第(3)步處理中，查找合計平衡差是否與另一方向上的非合計平衡差符號相反的情況，同樣不存在。

在第(4)步處理中，查找合計平衡差與同向的非合計平衡差符號相同的情況，處理結果如下：

此時，所有的平衡差已經都變為了0，說明各個方向上的計算已經恢復平衡，舍位平衡處理完成。如果仍未平衡，則需要進一步執行第(5)步處理。