您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要講解了“SLAM Noob的同時本地化和映射方法是什么”,文中的講解內容簡單清晰,易于學習與理解,下面請大家跟著小編的思路慢慢深入,一起來研究和學習“SLAM Noob的同時本地化和映射方法是什么”吧!
即時定位與地圖構建(simultaneous localization and mapping,簡寫成SLAM),用于環境模型(map)的并行構建,以及在其中移動的機器人的狀態估算。換句話說,SLAM為你提供了一種實時跟蹤機器人在世界上的位置、并識別地標(例如建筑物,樹木,巖石和其他世界特征)的位置的方法。除了本地化之外,我們還希望建立機器人環境的模型,這樣我們就有了一個物體的概念,以及圍繞機器人的地標,以便我們可以使用此地圖數據來確保機器人在世界各地移動時走在正確的道路上。因此,構建地圖的關鍵是機器人本身可能會由于其運動不確定性而失去對其位置的跟蹤,因為不存在現有的地圖,并且我們正在用機器人并行構建地圖。而這就是SLAM發揮作用的地方。
同時定位和地圖繪制(SLAM)的基礎是從機器人的傳感器和隨時間推移的運動中收集信息,然后使用有關測量和運動的信息來重建世界地圖。在這種情況下,我們將機器人定位在2D網格世界中,因此,基于圖的SLAM方法通過提取原始傳感器測量值來構造簡化的估計問題。這些原始測量值將替換為圖中的邊緣,然后可以將其視為虛擬測量值。 假設我們有一個機器人和初始位置 x0 = 0 和 y0 = 0 。對于此示例,為了保持簡單,我們并不關心方向。讓我們假設機器人在X方向上向右移動了10。所以,在理想世界中,你會了解到 x1,運動后的位置與x0 + 10相同,即x1 = x0 + 10,同理,y1與y0相同。
如圖,機器人在x方向上的位移為10:
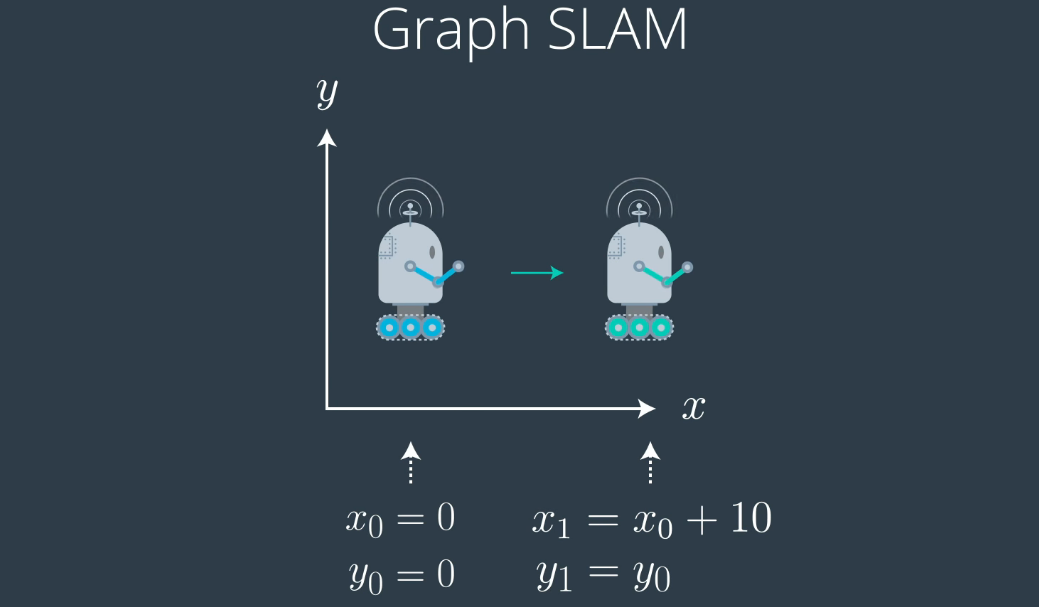
但是根據卡爾曼濾波器和其他各種機器人技術,我們已經知道位置實際上是不確定的。因此,與其假設我們的XY坐標系中的機器人精確地向右移動了10個位置,不如理解成它在x1 = x0 + 10運動更新后的實際位置是以(10,0)為中心的高斯分布,但是機器人也可能在其他地方。
如圖:運動更新后,高斯以機器人的位置為中心

這是x變量的高斯的數學公式: 當這兩個條件相同時,與其將x1設置為x0+10,不如用高斯函數來表示,此時高斯函數達到峰值。。因此,如果你減去x1-x0-10,把它變成一個正方形,然后將其轉換為高斯,我們將得到與x1和x0相關的概率分布。我們可以對y做同樣的轉換。根據我們的運動y不變,因此y1和y0盡可能靠近。

這兩個高斯的乘積現在是我們的約束條件。目標是在位置x0為(0,0)的情況下最大化位置x1的可能性。因此,Graph SLAM所做的是,它使用一系列此類約束條件來定義概率。 假設我們有一個在某個空間中移動的機器人,GRAPH SLAM會收集其初始位置(0,0),最初也稱為“初始約束”,然后收集許多相對約束,這些相對約束會將每個機器人姿態與之前的機器人姿態相關聯作為相對運動約束。例如,讓我們使用機器人可以在各個位置看到的地標,這是每次機器人看到地標時的相對測量約束。因此,Graph SLAM收集這些約束,以便找到最可能的機器人路徑配置以及地標位置,即映射過程。
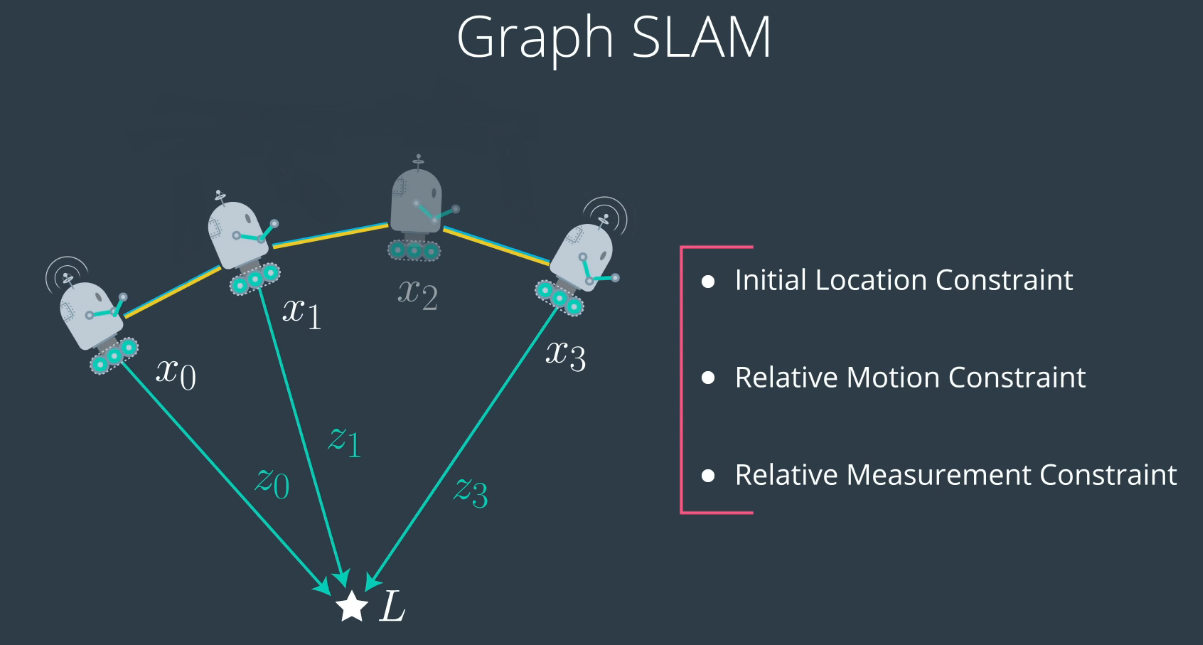
我們將生成一個帶有地標的2D世界網格,然后通過將機器人放置在該世界中,并在一定數量的時間步長上移動和感應來生成數據。實例化的機器人在世界中移動和感知時,將收集數據。我們的SLAM函數將把這些數據作為輸入。因此,讓我們首先創建此數據,并探索它如何代表我們的機器人進行運動和傳感器測量。
除了數據之外,我們的slam函數還具有:
N:機器人將要移動和感應的時間步數。
num_landmarks:世界上的地標數量。
world_size:你的世界的大小(w / h)。
motion_noise:與運動相關的噪聲;運動的更新置信度應為1.0/motion_noise.
measurement_noise:與測量/傳感相關的噪聲;測量的更新權重應為1.0/measurement_noise.
import numpy as np from helpers import make_data #slam的實現應該使用以下輸入 #請隨意更改這些輸入值并查看其響應方式! # 世界參數 num_landmarks = 5 # number of landmarks N = 20 # time steps world_size = 100.0 # size of world (square) # 機器人參數 measurement_range = 50.0 # range at which we can sense landmarks motion_noise = 2.0 # noise in robot motion measurement_noise = 2.0 # noise in the measurements distance = 20.0 # distance by which robot (intends to) move each iteratation # make_data實例化一個機器人,并為給定的世界大小和給定數量的地標生成隨機地標 data = make_data(N, num_landmarks, world_size, measurement_range, motion_noise, measurement_noise, distance)
讓我們編寫兩個主要功能,這些功能可以使機器人四處移動,幫助定位地標并在2D地圖上測量它們之間的距離:
Move:嘗試按dx,dy移動機器人。
Sense:返回可見范圍內地標的x和y距離。
class robot: #move function def move(self, dx, dy): x = self.x + dx + self.rand() * self.motion_noise y = self.y + dy + self.rand() * self.motion_noise if x < 0.0 or x > self.world_size or y < 0.0 or y > self.world_size: return False else: self.x = x self.y = y return True #sense function def sense(self): measurements = [] for landmark_index, landmark in enumerate(self.landmarks): landmark_distance_x = landmark[0] landmark_distance_y = landmark[1] random_noise = self.rand() cal_dx = self.x - landmark_distance_x + random_noise * self.measurement_noise cal_dy = self.y - landmark_distance_y + random_noise * self.measurement_noise is_not_in_measurement_range = self.measurement_range == -1 if(is_not_in_measurement_range) or ((abs(cal_dx) <= self.measurement_range) and (abs(cal_dy) <= self.measurement_range)): measurements.append([landmark_index, cal_dx, cal_dy]) return measurements
為了實現Graph SLAM,引入了一個矩陣和一個向量(分別為ω和xi)。矩陣是正方形的,標有所有機器人姿勢(xi)和所有地標。例如,每次進行觀察時,當你在兩個姿勢之間移動某個距離dx,并可以關聯這兩個位置時,可以將其表示為這些矩陣中的數值關系。 讓我們編寫函數,以便它為機器人的起始位置返回omega和xi約束。我們尚不知道的所有值都應使用0進行初始化。我們可以假設我們的機器人以100%的置信度在世界的正中間開始。
def initialize_constraints(N, num_landmarks, world_size): ''' This function takes in a number of time steps N, number of landmarks, and a world_size, and returns initialized constraint matrices, omega and xi.''' middle_of_the_world = world_size / 2 ## 建議:在變量中定義和存儲約束矩陣的大小(行/列) rows, cols = 2*(N + num_landmarks), 2*(N + num_landmarks) ## TODO: 用兩個初始“strength”值定義約束矩陣Omega omega = np.zeros(shape = (rows, cols)) ## 我們機器人最初的x,y位置 #omega = [0] omega[0][0], omega[1][1] = 1,1 ## TODO: Define the constraint *vector*, xi ## 假設機器人以100%的置信度在世界的正中間開始。 #xi = [0] xi = np.zeros(shape = (rows, 1)) xi[0][0] = middle_of_the_world xi[1][0] = middle_of_the_world return omega, xi
## slam接受6個參數并返回mu, ## mu是機器人穿過的整個路徑(所有x,y姿勢)和所有地標位置 def slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise): ## TODO: 使用你的初始化創建約束矩陣 omega, xi = initialize_constraints(N, num_landmarks, world_size) ## TODO:遍歷數據中的每個時間步驟 for time_step in range(len(data)): ## 每次迭代時獲取所有的運動和測量數據 measurement = data[time_step][0] motion = data[time_step][1] x dx = motion[0] # 本次沿x移動的距離 dy = motion[1] # 本次沿y移動的距離 #假設機器人在這個時間從(x0,y0)移動到(x1,y1) #omega的偶數列對應于x值 x0 = (time_step * 2) #x0 = 0,2,4,... x1 = x0 + 2 #x1 = 2,4,6,... # omega 的奇數列對應于y值 y0 = x0 + 1 #y0 = 1,3,5,... y1 = y0 + 2 #y1 = 3,5,7,... actual_m_noise = 1.0/measurement_noise actual_n_noise = 1.0/motion_noise ## TODO: 更新約束矩陣/向量(Omega/xi)以解釋所有*measurements* ## 這應該是一系列考慮測量噪聲的附加值 for landmark in measurement: lM = landmark[0] # 地標 id dx_lM = landmark[1] # 沿x與當前位置分離 dy_lM = landmark[2] # 沿y與當前位置分離 L_x0 = (N*2) + (lM*2) # 偶數列有x個地標值 L_y0 = L_x0 + 1 # 奇數列有y個地標值 # 更新對應于x0和Lx0之間測量值的omega值 omega[x0][x0] += actual_m_noise omega[L_x0][L_x0] += actual_m_noise omega[x0][L_x0] += -actual_m_noise omega[L_x0][x0] += -actual_m_noise # 更新對應于y0和Ly0之間測量值的omega值 omega[y0][y0] += actual_m_noise omega[L_y0][L_y0] += actual_m_noise omega[y0][L_y0] += -actual_m_noise omega[L_y0][y0] += -actual_m_noise # 更新X0和LX0之間的測量值對應的xi值 xi[x0] -= dx_lM/measurement_noise xi[L_x0] += dx_lM/measurement_noise # 更新y0和Ly0之間的測量值對應的xi值 xi[y0] -= dy_lM/measurement_noise xi[L_y0] += dy_lM/measurement_noise ## TODO: 更新約束矩陣/向量(omega/XI),以解釋從(x0,y0)到(x1,y1)和運動噪聲的所有*運動*。 omega[x0][x0] += actual_n_noise omega[x1][x1] += actual_n_noise omega[x0][x1] += -actual_n_noise omega[x1][x0] += -actual_n_noise omega[y0][y0] += actual_n_noise omega[y1][y1] += actual_n_noise omega[y0][y1] += -actual_n_noise omega[y1][y0] += -actual_n_noise xi[x0] -= dx/motion_noise xi[y0] -= dy/motion_noise xi[x1] += dx/motion_noise xi[y1] += dy/motion_noise ## TODO: 在遍歷所有數據之后 ## 計算姿勢和地標位置的最佳估計值 ##使用公式,omega_inverse * Xi inverse_of_omega = np.linalg.inv(np.matrix(omega)) mu = inverse_of_omega * xi return mu
讓我們打印函數產生的估計姿勢和界標位置。我們定義了一個提取姿勢和地標位置,并將它們作為自己的單獨列表返回。
def get_poses_landmarks(mu, N):
# 創建一個姿勢列表
poses = []
for i in range(N):
poses.append((mu[2*i].item(), mu[2*i+1].item()))
# 創建一個地標列表
landmarks = []
for i in range(num_landmarks):
landmarks.append((mu[2*(N+i)].item(), mu[2*(N+i)+1].item()))
# 返回完成的列表
return poses, landmarks
def print_all(poses, landmarks):
print('\n')
print('Estimated Poses:')
for i in range(len(poses)):
print('['+', '.join('%.3f'%p for p in poses[i])+']')
print('\n')
print('Estimated Landmarks:')
for i in range(len(landmarks)):
print('['+', '.join('%.3f'%l for l in landmarks[i])+']')
# 調用你的slam實現,并傳入必要的參數
mu = slam(data, N, num_landmarks, world_size, motion_noise, measurement_noise)
# 打印出地標和姿勢結果
if(mu is not None):
# 獲取姿勢和地標列表
# 并打印出來
poses, landmarks = get_poses_landmarks(mu, N)
print_all(poses, landmarks)如圖:估計的機器人姿勢和地標 
# 導入函數
from helpers import display_world
# 顯示最終世界!
# 定義圖形大小
plt.rcParams["figure.figsize"] = (20,20)
# 檢查姿勢是否已創建
if 'poses' in locals():
# 打印出最后一個姿勢
print('Last pose: ', poses[-1])
# 顯示機器人的最后位置和地標位置
display_world(int(world_size), poses[-1], landmarks)如圖:輸出量 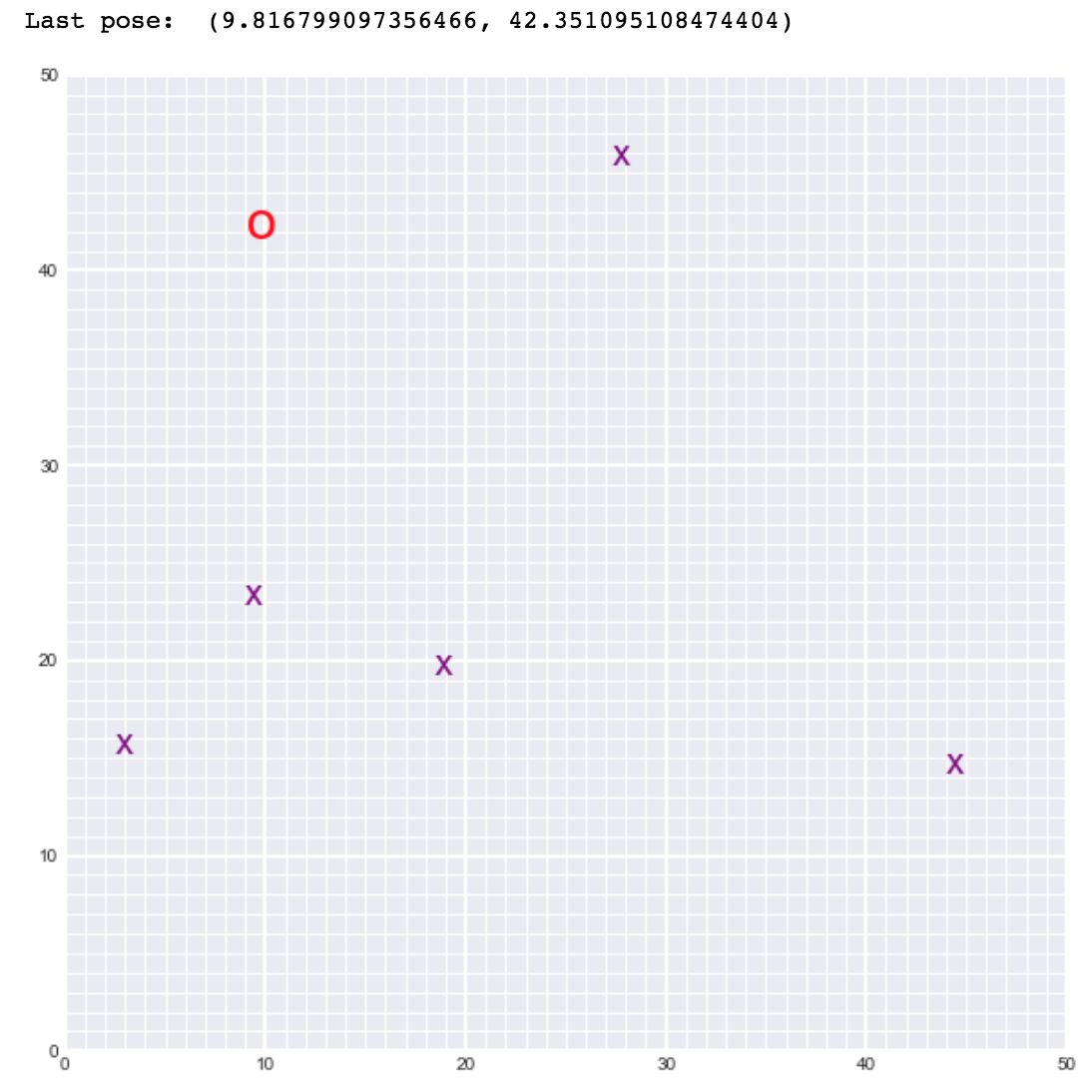
感謝各位的閱讀,以上就是“SLAM Noob的同時本地化和映射方法是什么”的內容了,經過本文的學習后,相信大家對SLAM Noob的同時本地化和映射方法是什么這一問題有了更深刻的體會,具體使用情況還需要大家實踐驗證。這里是億速云,小編將為大家推送更多相關知識點的文章,歡迎關注!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。