您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章給大家分享的是有關ID3、C4.5、CART三種決策樹的區別是什么的內容。小編覺得挺實用的,因此分享給大家做個參考,一起跟隨小編過來看看吧。
一棵決策樹包含一個根結點、若干個內部結點和若干個葉結點;葉結點對應于決策結果,其他每個結點則對應一個屬性測試;每個結點包含的樣本結合根據屬性測試的結果被劃分到子結點中;根結點包含樣本全集,從根結點到每個葉結點的每個葉結點的路徑對應一個判定測試序列。決策樹學習的目的是為了產生一棵泛化能力強,也就是能夠處理未見實例的決策樹。
信息熵是度量樣本集合純度最常用的一種指標。假設樣本集合D中第k類樣本所占的比重為pk,那么信息熵的計算則為下面的計算方式
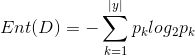
當這個Ent(D)的值越小,說明樣本集合D的純度就越高
有了信息熵,當我選擇用樣本的某一個屬性a來劃分樣本集合D時,就可以得出用屬性a對樣本D進行劃分所帶來的“信息增益”
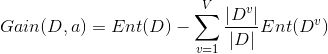
一般來講,信息增益越大,說明如果用屬性a來劃分樣本集合D,那么純度會提升,因為我們分別對樣本的所有屬性計算增益情況,選擇最大的來作為決策樹的一個結點,或者可以說那些信息增益大的屬性往往離根結點越近,因為我們會優先用能區分度大的也就是信息增益大的屬性來進行劃分。當一個屬性已經作為劃分的依據,在下面就不在參與競選了,我們剛才說過根結點代表全部樣本,而經過根結點下面屬性各個取值后樣本又可以按照相應屬性值進行劃分,并且在當前的樣本下利用剩下的屬性再次計算信息增益來進一步選擇劃分的結點,ID3決策樹就是這樣建立起來的。
C4.5決策樹的提出完全是為了解決ID3決策樹的一個缺點,當一個屬性的可取值數目較多時,那么可能在這個屬性對應的可取值下的樣本只有一個或者是很少個,那么這個時候它的信息增益是非常高的,這個時候純度很高,ID3決策樹會認為這個屬性很適合劃分,但是較多取值的屬性來進行劃分帶來的問題是它的泛化能力比較弱,不能夠對新樣本進行有效的預測。
而C4.5決策樹則不直接使用信息增益來作為劃分樣本的主要依據,而提出了另外一個概念,增益率
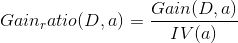
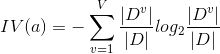
但是同樣的這個增益率對可取值數目較少的屬性有所偏好,因此C4.5決策樹先從候選劃分屬性中找出信息增益高于平均水平的屬性,在從中選擇增益率最高的。
CART決策樹的全稱為Classification and Regression Tree,可以應用于分類和回歸。
采用基尼系數來劃分屬性
基尼值
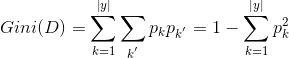
基尼系數

因此在候選屬性中選擇基尼系數最小的屬性作為最優劃分屬性。
感謝各位的閱讀!關于“ID3、C4.5、CART三種決策樹的區別是什么”這篇文章就分享到這里了,希望以上內容可以對大家有一定的幫助,讓大家可以學到更多知識,如果覺得文章不錯,可以把它分享出去讓更多的人看到吧!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。