您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
今天給大家介紹一下Harris特征點是什么。文章的內容小編覺得不錯,現在給大家分享一下,覺得有需要的朋友可以了解一下,希望對大家有所幫助,下面跟著小編的思路一起來閱讀吧。
1)Moravec算子各向異性響應
Moravec算子僅僅在8個方向(水平、垂直和四個對角方向)計算灰度變化,為了對其擴展,有必要設計一個可以在任何方向對灰度變化進行測度的函數。1988年,Harris和Stephen通過對Moravec算子進行展開,推導得到了Prewitt算子,也即Harris算子。
我們先來看看與Harris相關的背景知識。通常,Prewitt算子被用來對圖像的梯度進行近似。然而,在實際應用中,一階梯度通過下圖中的公式來進行近似:
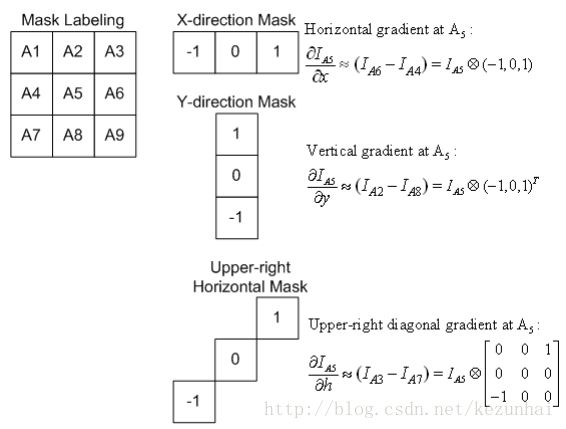
對Morevec算子進行分析可以得到:兩個Morevec窗口中對應像素差的和可以作為圖像梯度的合理近似。我們再來看下圖:

通過對上圖的分析,我們有可以進一步得到:morevec算子中的灰度變化可以采用圖像梯度進行近似。
通過上面的分析,灰度的變化可以表示為圖像梯度的函數,公式表示如下:

其中,(u,v)表示滑動,x方向為(1,0),y方向為(0,1),微分的計算如上圖所示。
到這里,大家非常明了:上式可以對moravec算子中的灰度變化計算進行精確的逼近。但是又與Moravec算子中灰度變化不同的是通過合理的選擇(u,v)可以對任何方向的灰度變化進行測度。
2)噪聲響應
在Moravec算子中,滑動窗采用的是方形的,方形窗使得不同方向上的中心像素與邊界像素的歐式距離是變化的。為了克服這個問題,Harris&Stephen提出只需將方向窗改成圓窗。同時,窗中的每個像素是同等地位的,理論上應該是離中心越近的權重越大,而離中心越遠,權重越小,因此我們加入高斯權重。因此,灰度變化的新測度方式可以通過下圖來表示:
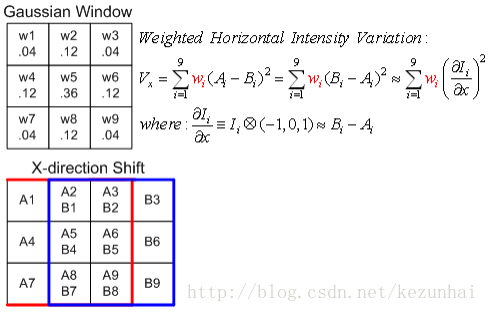
通過公式表示如下:
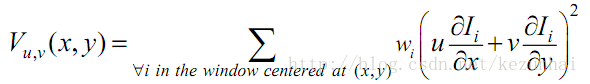
其中,wi表示位置i處的高斯權重。
邊緣的強響應
因為Moravec算子在邊緣處很容易出現誤檢,Harris&Stephen通過考慮不同方向的灰度度量形成新的角度性測度(cornerness measure)。接著,我們對上面的式子進行變換,如下式:
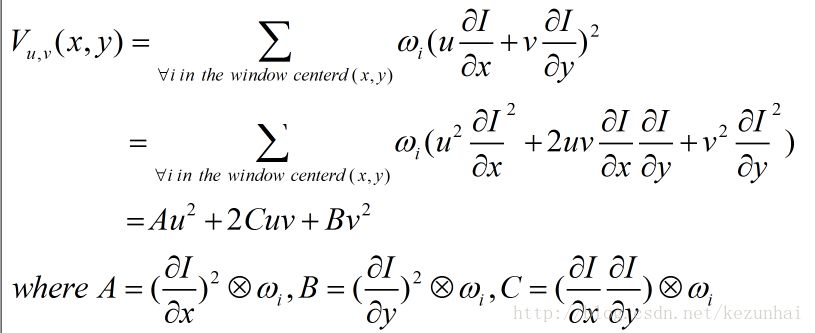
Harris&Stephen同時也注意到,上式可以寫成:
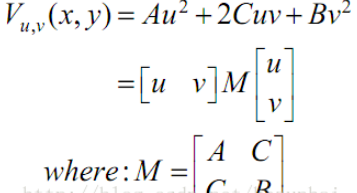
對上面的矩陣M,其特征值與圖像表面的主曲率是成正比的,并且形成了對M的旋轉不變的描述(Proportional to the principle curvature of the image surface and form a rotationally invariant description of M)。然后,由于M是通過水平和垂直方向的梯度來近似的,他們不是真正的旋轉不變。
同樣,與Moravec算子一樣,我們再來看下面的四張張圖:
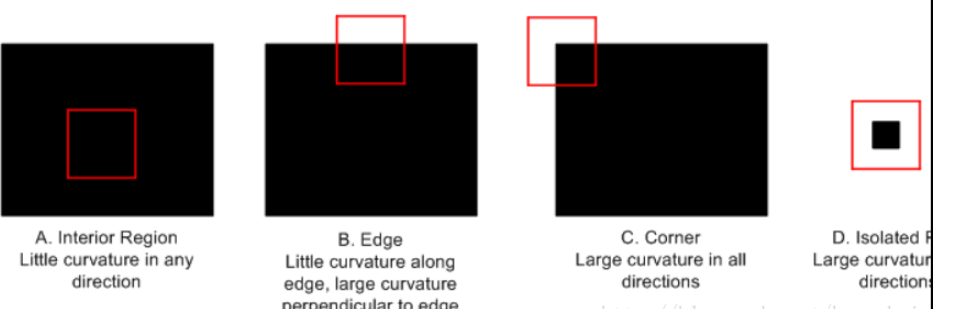
圖中A表示在一個物體的內部或背景上,窗口內的灰度值相對不變,因此該窗口表面上幾乎沒有曲率,因此M的特征值相對很小;B窗口在一個邊緣處,垂直于邊緣的地方將有明顯很大的曲率,而平行于邊緣的地方幾乎沒什么曲率,因此該形式下M的特征值一個會比較大,另一個較小;C和D對應于角度和離散點,在兩個方向都會有很大的曲率,因此,M的特征值都將會很大。假設r1和r2是M的兩個特征值,通過上面的分析,可以將一個平面表示為以下三個可區分的區域:
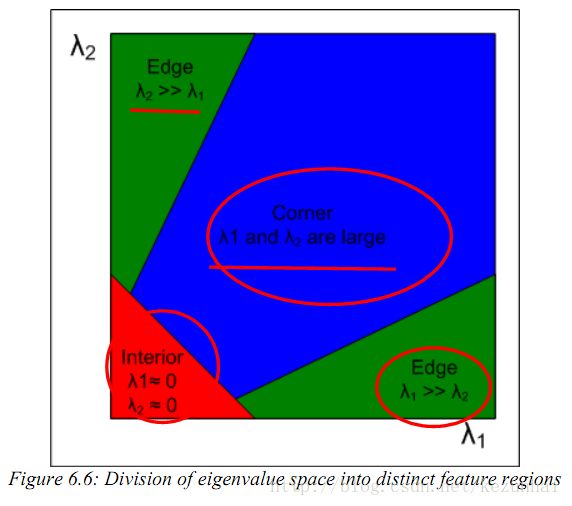
Harris&Stephen提出下面的角點性測度: k一般取值04~0.6。
最后,我們來總結下Harris算子的計算步驟:
( 1)對每一個像素計算自相關矩陣M
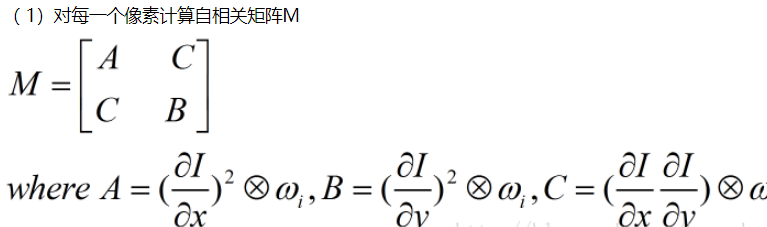
(2)構造角點性映射圖(Construct cornerness map)
(3)閾值化,對得到的C(x,y)進行閾值
(4)非極大值抑制
以上就是Harris特征點是什么的全部內容了,更多與Harris特征點是什么相關的內容可以搜索億速云之前的文章或者瀏覽下面的文章進行學習哈!相信小編會給大家增添更多知識,希望大家能夠支持一下億速云!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。