1 二分圖

二分圖：又稱作二部圖，是圖論中的一種特殊模型。 設G=(V,E)是一個無向圖，如果頂點V可分割為兩個互不相交的子集(A,B)，并且圖中的每條邊   所關聯的兩個頂點i和j分別屬于這兩個不同的頂點集(i∈A, j∈B)，則稱圖G為一個二分圖。  

簡單來說，如果圖中所有頂點可以被分為兩個集合，圖中所有的邊的頭和尾不屬于同一個頂點集合，而是跨越兩個集合，則這個圖是一個二分圖。

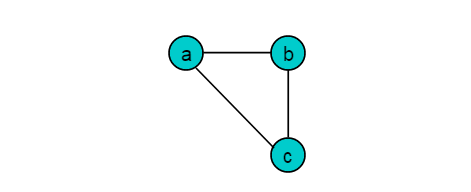
例如：圖1.1所示的圖，無論如何劃分頂點集合，也不能保證所有邊的頭和尾隸屬于不同集合，因此，圖1.1所示的圖不是二分圖。

 

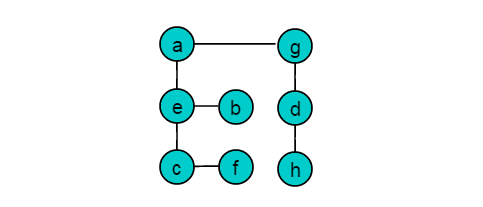
例如：圖1.2所示的無向圖：

 

將頂點a，b，c，d作為集合A，將e，f，g，h作為集合B，將圖1.2轉化為圖1.3所示：

 

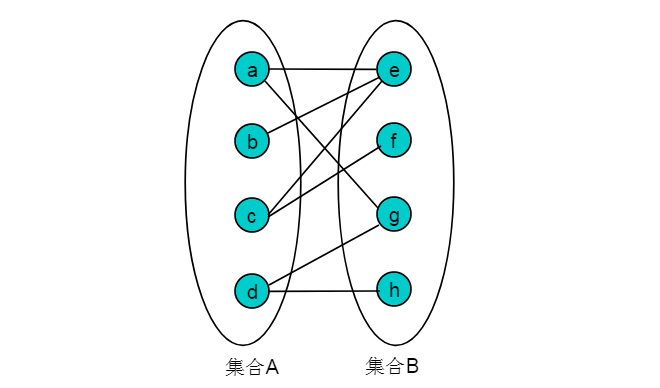
可以看出，圖中頂點可以劃分為A，B兩個集合，而任意一條邊的頭和尾又分別隸屬于集合A和集合B，因此，此圖為二分圖。

2 匹配

匹配：在圖論中，一個匹配（matching）是指一個邊的集合，其中任意兩條邊都沒有公共頂點。
例如：圖2.1中紅色的邊，可以為圖1.3所示圖的一個匹配。

 

3 最大匹配

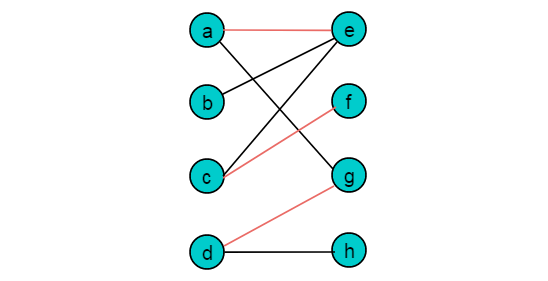
最大匹配：一個圖所有匹配中，所含匹配邊數最多的匹配，稱為這個圖的最大匹配。圖 3.1是一個最大匹配，它包含4條匹配邊。

 

4 完美匹配

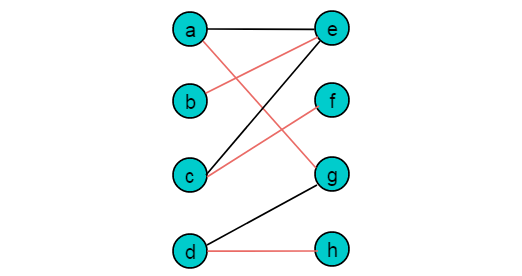
完美匹配：如果一個圖的某個匹配中，所有的頂點都是匹配點，那么它就是一個完美匹配。完美匹配一定是最大匹配（完美匹配的任何一個點都已經匹配，添加一條新的匹配邊一定會與已有的匹配邊沖突），但并非每個圖都存在完美匹配。

5 交替路徑

交替路徑：從一個未匹配點出發，依次經過非匹配邊、匹配邊、非匹配邊…形成的路徑稱為交替路徑。

6 增廣路徑

增廣路徑：從一個未匹配點出發，走交替路，如果途徑另一個未匹配點（出發的點不算），則這條交替路稱為增廣路（agumenting path）。

增廣路徑性質：
????（1）P的路徑長度必定為奇數，第一條邊和最后一條邊都不屬于M，因為兩個端點分屬兩個集合，且未匹配。
????（2）P經過取反操作可以得到一個更大的匹配M’。
????（3）M為G的最大匹配當且僅當不存在相對于M的增廣路徑。

7 匈牙利算法

匈牙利算法：利用增廣路徑求二分圖的最大匹配算法稱作匈牙利算法。（匈牙利數學家Edmonds于1965年提出）。
基本思想：通過尋找增廣路徑，把增廣路徑中的匹配邊和非匹配邊的相互交換，這樣就會多出一條匹配邊，直到找不到增廣路徑為止。

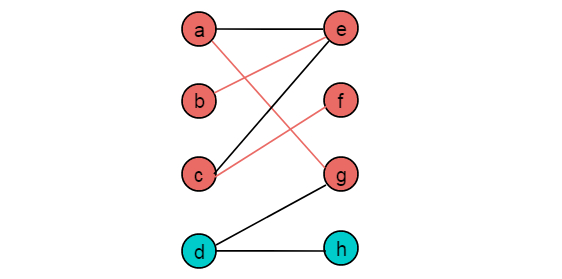
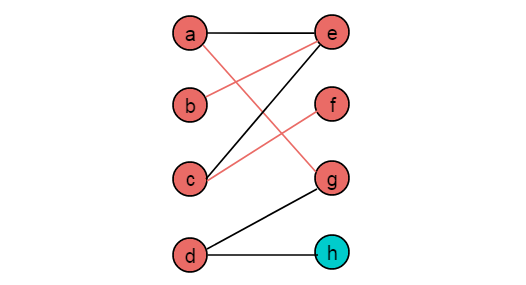
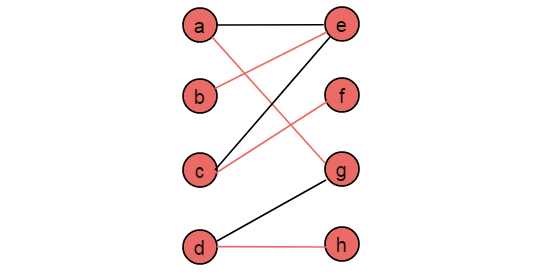
例如：以圖2.1所示的二分圖為例，使用匈牙利算法求解圖的最大匹配。
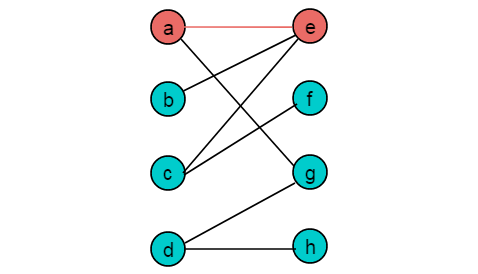
（1）從頂點a出發，按照交替路徑前進，第一個非匹配邊為       ，到達頂點e，e為非匹配點，構成增廣路徑。令          為匹配邊，頂點a，e為匹配頂點。    
   

 

，到達頂點e，選擇匹配邊，到達a，選擇非匹配邊          ，g為非匹配點，找到一條增廣路徑。    
   

   

（3）交換增廣路徑中的匹配邊與非匹配邊，得到如下匹配。    
   

   

（4）從頂點c出發，第一非匹配邊為，到達頂點e，然后按照交替路徑前進，到達頂點b，無法繼續前進。      
     

     

（5）從頂點c出發，選擇第二條非匹配邊。      
     

     

（6）從頂點d出發，選擇非匹配邊，到達頂點g，選擇匹配邊，到達頂點a，選擇非匹配邊到達頂點e，選擇匹配邊，到達頂部b，沒有可以選擇的邊，且沒有找到增廣路徑。          
         

         

（7）繼續從頂點d出發，選擇非匹配邊，找到增廣路徑，將邊變為匹配邊，算法結束。

8 結語

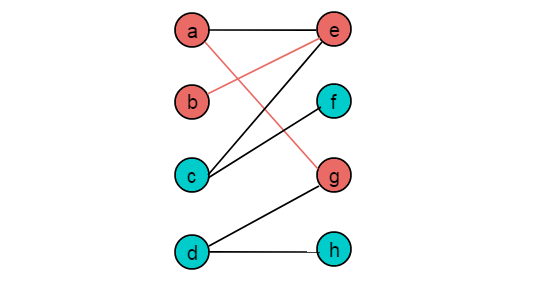
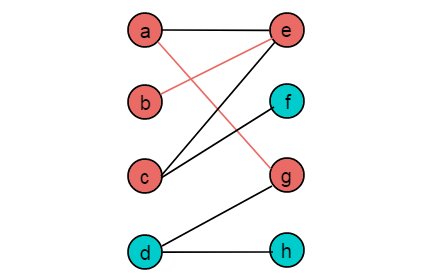
匈牙利算法多用于指派問題中，例如任務匹配問題。通過轉化為二分圖的形式，求解最大匹配，保證實現最優分配。