一、二分法

二分法的思想很簡單，就是從0到N不斷的去縮小范圍來找一個一個滿足精度的最佳值。我們舉一個函數的例子：

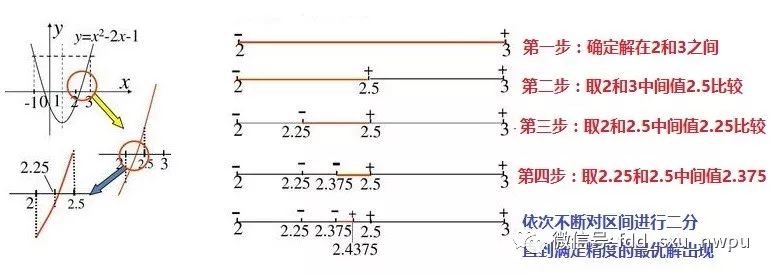
這就是二分法的思想，求平方根也是，我們從0到value取出中間值，然后不斷地比較，假設value=10，查找區間為（0，10），這時候取（0,10）的中間值mid=5，mid*mid再和value比較之后，確定下一次查找的區間變為（0，5），依次類推。一直到滿足我們需要的精度即可。下面我們使用java代碼實現一下：

    static double MySqrt(int value, double t){
        if (value < 0 || t<0)
            return 0;
        double left = 0;
        double right = value;
        double mid = (right + left) / 2;
        double offset = 2*t ;
        while (offset>t){
            double temp = mid*mid;
            if (temp > value){
                right = (left + right) / 2;
                offset = temp - value;
            }
            if (temp <= value){
                left = (left + right) / 2;
                offset = value - temp;
            }
            mid = (left + right) / 2;
        }
        return mid;
    }

在這里value就是我們要求的數字，t表示的是精度。這個方法在這，大家可以測試一遍。不過在這里有一個小小的問題需要我們去注意：

如果我們對整數9取平方根，結果不是3，這里有精度損失，損失的原因之一是和計算機有關的，因為計算機的底層其實只有0和1，所以會無限的接近，而不能精確表示。

以上就是二分法求解的思想，這個思想很簡單，不過實現的方法卻是有一點點麻煩。在這里我們開始介紹第二種方法，那就是牛頓的微積分思想

二、牛頓迭代法

牛頓的微積分的思想就是無限接近，在這里提一句，如果你是數學大佬就不要追究思想到底是啥了。對于求平方根來說，使用切線來無限逼近的方式有時候能起到意想不到的效果。

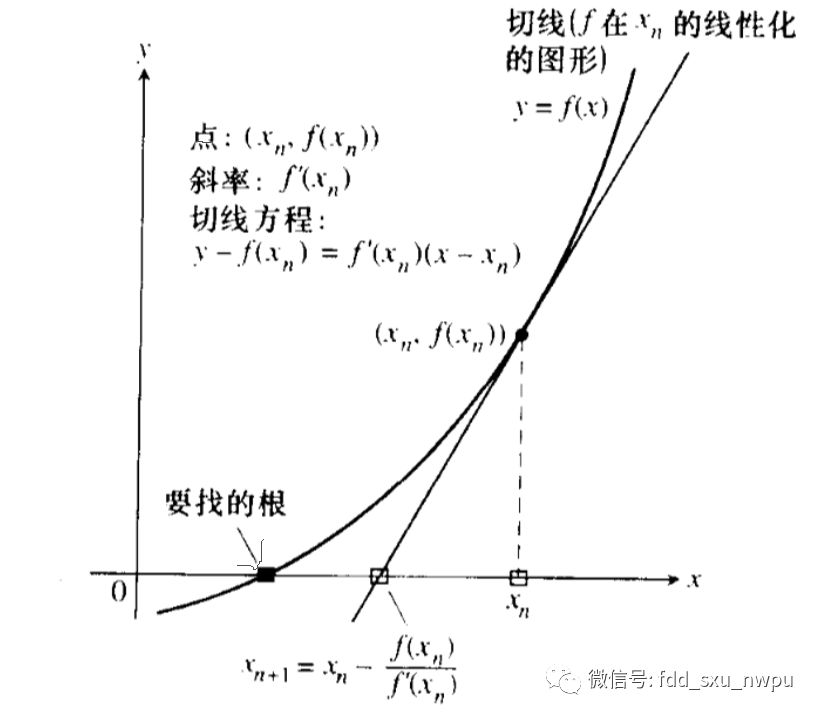
設r是f(x) = 0的根，選取x0作為r初始近似值，過點（x0,f(x0)）做曲線y = f(x)的切線L，

L的方程為y = f(x0)+f'(x0)(x-x0)，求出L與x軸交點的橫坐標 x1 = x0-f(x0)/f'(x0)，稱x1為r的一次近似值。

過點（x1,f(x1)）做曲線y = f(x)的切線，并求該切線與x軸交點的橫坐標 x2 = x1-f(x1)/f'(x1)，稱x2為r的二次近似值。

重復以上過程，得r的近似值序列，其中x(n+1)=x(n)－f(x(n))/f'(x(n))，稱為r的n+1次近似值，上式稱為牛頓迭代公式。

我們使用一張圖來演示一下：

這種方式也很好理解。所以我們直接來看實現：

static double SqrtIterator(int value,double t){
    double temp = value;
    while (fabs(temp*temp-value)>t){
        temp=(temp+value/temp) / 2.0;
    }
    return temp;
}
//取絕對值
private static double fabs(double a) {
    return (a < 0) ? -a : a;
}