您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
數學相關的知識:
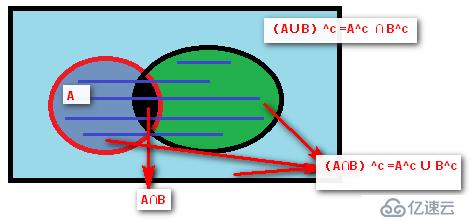
集合:是指具有某種特定性質的事物的總體,組成集合的事物稱為元素。
?通常使用大寫表示集合,小寫表示元素;列舉法,描述法
?列舉法:A={a1,a2,a3,...,an},a1∈A
?描述法:B={x|x^2-1=0},{x|x具有的性質},方程的解即是組成B集合元素
函數
奇偶函數:f(-x)=-f(x),f(x)=f(-x)
初等函數:
冪函數:y=X^u u∈常數
指數函數:y=a^x;(a>0且a≠0)
對數函數:y=logaX (a>0且a≠0,a=e時y=ln x)
三角函數:y=sin x ,y=cos x,y=tan x
反三角函數:y=arcsin x,y=arccos x,y=arctan x閉區間連續函數的性質
有界性與最大值和最小值定理
區間I上有定義的f(x),x0∈I,使得對于任一x∈I,都有f(x)≤f(x0),f(x0)≥f(x),即f(x0)是f(x)在區間I上的最大值和最小值。
導數
切線問題,在曲線上取一點M(x0,y0),當在曲線取另外一點N任意變化,但直線與曲線線切時,即相交于一點,|MN|->0,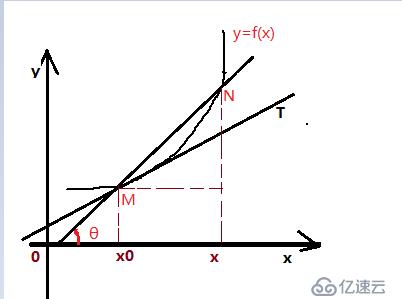
MN直線的斜率:tanθ=(y-y0)/(x-x0)=[f(x)-f(x0)]/(x-x0)
既有但x->x0時此時直線與曲線線切
?f `(x0)=lim(△y/△x)=lim [ f(x0+△x) - f(x0)] / △x
?也可記作:y*|x=x0 ,dy/dx |x=x0
導數幾何意義:切線的斜率
常用初等函數導數
1.(C)'=0
2.(x^u)'=ux^(u-1)
3.(sinx)'=cosx
4.(cosx)'=-sinx
5.(tanx)'=sec^2 x
6.(cotx)'=-csc^2 x
7.(a^x)'=a^x *lna
8.(e^x)'=e^x
9.(logaX)'=1/(x*lna)
10.(lnx)'=1/x
11.(1/x)'=1/(x^2)求導法則:復合函數求導
[ u(x) ± v(x) ] ' =u'(x) ± v'(x)
[ u(x)·v(x) ] ' =u'(x)v(x) + u(x)v'(x)
[ u(x) / v(x) ] '= [ u'(x)v(x) - u(x)v'(x) ] / v^2(x)
dy/dx=(dy/du)*(du/dx)
微分定義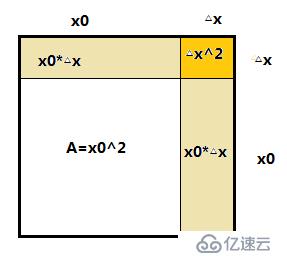
設此薄片的邊長為x0,面積為A,由于薄片受溫度變化的影響時面積發生改變,對應長度增加△x,此時面積對應增加△A
△A=(x0+△x)^2 - x0^2=2x0△x + (△x)^2
==>一般的:△y=A△x + 0(△x)--->替代(△x)^2即(△x)很小時,
當△x高階無窮小時A≠0,△y=A△x
函數表示為:△y=f(x0+△x) - f(x0)=A△x + 0(△x),稱函數y=f(x)在點x0是可微的,而A△x叫做函數在點x0相應于自變量△x的微分,記作dy ,dy=A△x
當△x-->0時;△y/△x=A+ o(△x)/△x ==>A=lim (△y/△x)=f '(x0)由此可見函數f(x)在x0處可微的充分必要條件是函數在點x0處可導:dy=f '(x0)△x-->dy=f '(x)dx

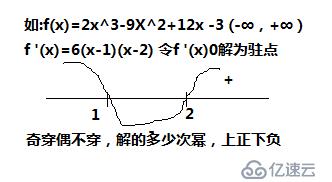
偏導數
?研究一元函數時,我們從研究函數變化率引入了導數概念,對于多元函數同樣研究它的變化率,但多元函數的自變量不止一個,因變量與自變量比一元函數復雜多。這時自變量當個逐一考慮,另外的自變量當做常數考慮。這時的導數稱為偏導數。與一元函數定義類似。
?對應一元的微分,多元引入全微分:dz=(?z/?x)·△x+(?z/?y)·△y :△x-->dx
?二元函數的極值問題,一般可以利用偏導數來解決,跟一元類似處理。
多元函數與一元函數類似,我們可以利用函數的極值來求函數的最大值和最小值
例如:某廠要用鋼板做成一個體積為2立方米的有蓋長方形水箱。問當長寬高各取什么樣的尺寸才最省材料?
?設長x m,寬y m,高為2/(xy)
?A=2( xy+y2/(xy) +x2/(xy) ),(x>0,y>0)
?Ax=2(y-2/(x^2))=0,Ay=2(x-2/(y^2))=0==>x y的值
| 順序編號i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 時間ti/h | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 刀具厚度yi/mm | 27.0 | 26.8 | 26.5 | 26.3 | 26.1 | 25.7 | 25.3 | 24.8 |
為了確定時間與刀具厚度的關系,描點法在直角坐標系觀察數據: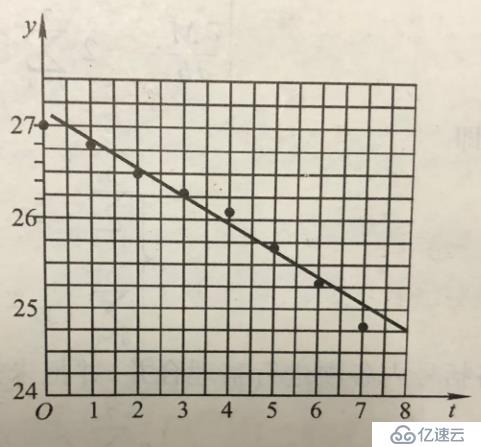
圖中點大致接近于直線,線性負相關,可以設:f(t)=at+b,a,b常數
?因為這些點本來就不在一條直線上,那么只能要求函數在實驗各點的取值盡量與實驗的結果相差都很小,即要使各點誤差最小:▲=yi-f(ti) (i=0,1,2,...7)
是否可以通過偏差求和來保證每個偏差最小:∑[yi-f(ti)] (i=0,1,2,...7) ?,從圖中可以看出數據點分布在直線兩側,若通過求和方法,偏差有正負之分,會相互抵消。可通過取絕對值避免抵消偏差:∑ |yi-f(ti)]| (i=0,1,2,...7),但不便于分析討論。任何實數的平方都是正數或零:M=∑[yi-f(ti)]^2 (i=0,1,2,...7) 這種方法即最小二乘法。
?這時即求何時M取最小值,a,b為何值:由于yi,ti已知,把函數歸結為M=M(a,b)求解,自變量看作a,b:上述的偏導數極值討論:
?Ma(a,b)=0
?Mb(a,b)=0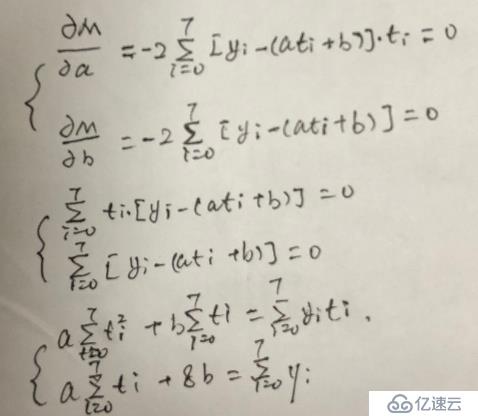

?此時計算出a,b相關項即可求出:y=at+b**
向量:既有大小又有方向(矢量)
向量的大小叫做向量的模;注這里粗體表示向量,i, j, k空間直角坐標系單位向量
向量線性運算:起點-->終點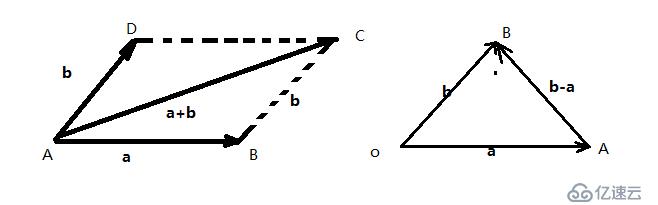
a+b=AB+BC=c
b+a=AD+DC=AC
AB=AO+OB=OB-OA=b-a
設a=(ax,ay,az) b=(bx,by.bz)==> a=axi+ayj+azk
a+b等于對應坐標相加
向量的模-勾股定理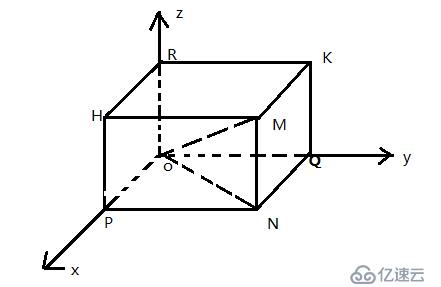
設 r=(x,y,z)=OM ,OP=xi ,OQ=yi ,OR=zi
OM=OP+OQ+OR
|r|=|OM|=√[|OP|^2+|OQ|^2+|OR|^2 ]
|r|=√x^2+y^2+z^2

對數運算
性質: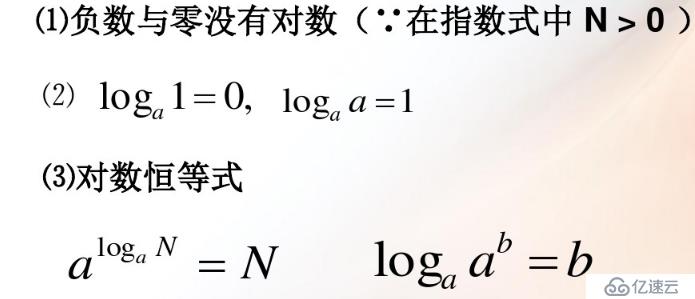
對數的乘法性質:log(ab)=loga+logb
對數的除法性質:log(a/b)=loga-logb
對數的乘方性質:log(b^n)=(n/m)logb ,m為對數底的乘方
換底公式:log(b)=log(b)/log(a)
常用的有:log(b)=log(b)/log(a) (以10為底)
log(b)=ln(b)/ln(a) (以e為底)linux中使用:
log( x ) 返回 x 的自然對數e
如求10的自然對數:
awk 'BEGIN { fl=log(10); print fl }'
如果求log(2,10),以2為底,10的對數:
awk 'BEGIN { fl=(log(10)/log(2)); print fl }'
#awk 'BEGIN{a=(log(4)/log(2));printf "%d\n" ,a/0.5}'矩陣
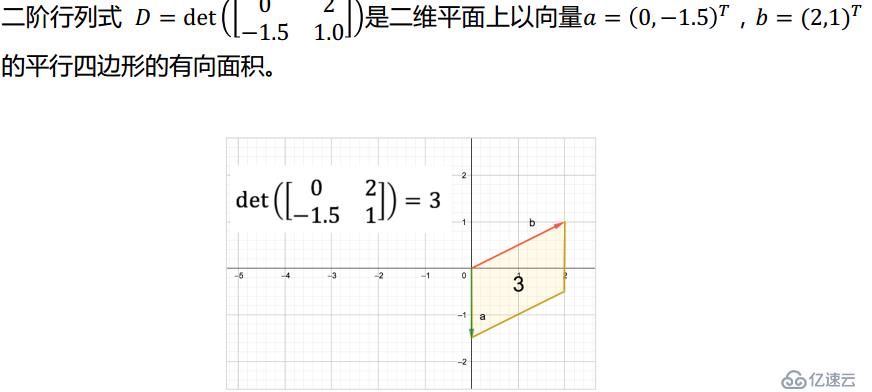
行列式運算
主對角線-副對角線
高階轉換為低階3--》2
在三階行列式中,將元素aij所在的第i行和第j列劃去后,剩下的元素按元次序構成二階行列式,稱為aij的代數余子式,記為Mij,余子式前再冠之符號(-1)的(i+j)次方
則三階行列式的值等于該行列式的任意一行或一列的所有元元素與他們的代數余子式乘積之和。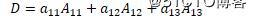
克拉默法則解線性方程
高斯消元法,n個未知變量和方程如何求解
注:克拉默法則只適用于未知數的個數與方程的個數相等的線性方程組,若不相等時不適用該法則。
推論:
如果齊次線性方程組有非零解,則其系數行列式D必須等于0.


免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。