溫馨提示×
您好，登錄后才能下訂單哦！
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好，登錄后才能下訂單哦！
本篇文章給大家分享的是有關最短路徑Dijkstra的圖示化證明是怎么樣的，小編覺得挺實用的，因此分享給大家學習，希望大家閱讀完這篇文章后可以有所收獲，話不多說，跟著小編一起來看看吧。
先看圖，后面分析
現在將圖與之前學的最短路徑證明算法聯系起來。
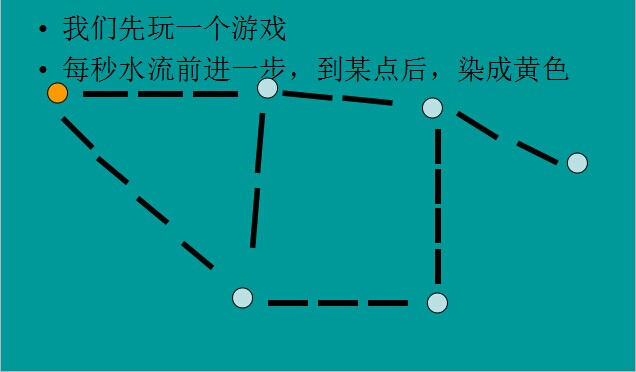
首先起點A是水立刻到達的，假設剩下的一些點B,C,D,E,F全部是村莊，
那么此時遭受水淹的危險的村莊是與起點直接相連的2個節點B和C.
我們此時可以算出這2個節點與起點A的最短距離。
此時這2個節點中最短距離就是水最先淹沒的村莊，在圖中是B.
也就是過了3秒鐘后，B被染成了黃色。
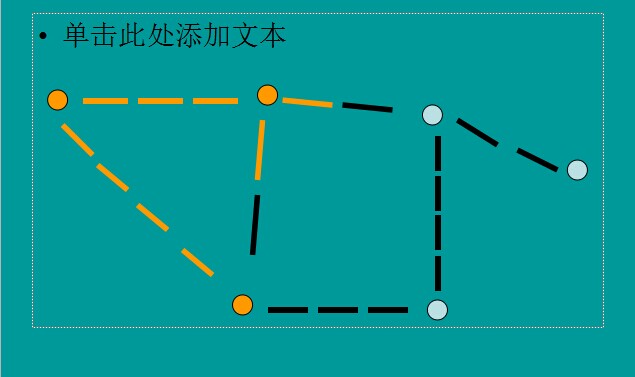
進入下一個階段，既然B被淹沒，此時與B直接相連的2個節點C和D都是下一步被淹沒的村莊之一。
因為B的水正在向它們流動。
但是這里不要忘記A的水之前已經在向C流動了，
所以，我們稱，與A和B系統直接相連的所有節點(C,D)是下一步可能遭受威脅的節點群。
這就是為什么當B被染成黃色后，要重新計算C先遭受B的水淹沒的可能性大還是遭受A的水淹沒的可能性大。放在算法里就是重新計算路徑。
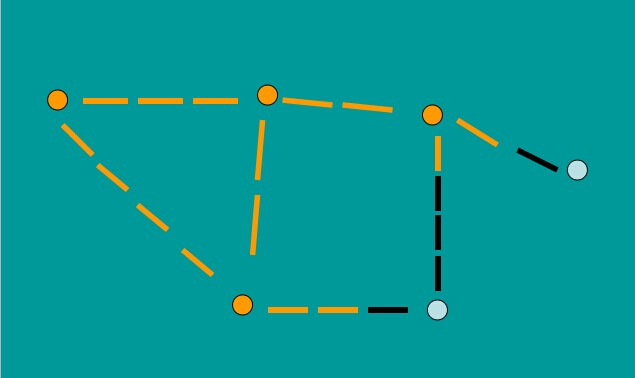
這里，C節點先遭受A的水淹沒。那么此后B的水再來也無濟于事，C已經被淹沒了。
當C淹沒后，與C直接相連的節點E也就被加入潛在淹沒村莊群了。
此時潛在淹沒村莊群的集合是(D,E).
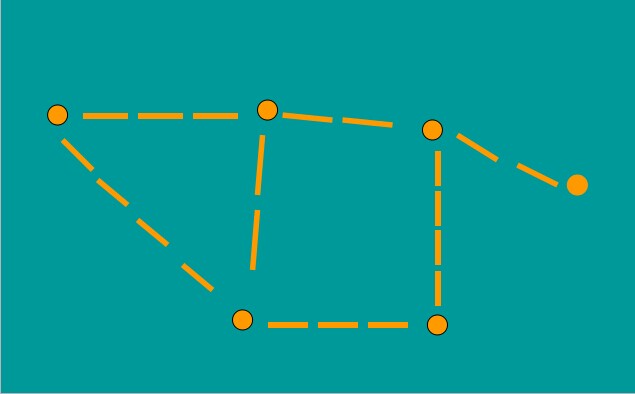
此時就可以重新計算(D,E) 中每個節點通過已經淹沒群(A,B,C)與A的距離。
實際上每次只要計算最后一個加入的節點對潛在淹沒村莊群的影響就可以。
按照這樣的思路，你是否對算法里的最短路徑Dijkstra有了更深的理解了呢？
不用死記硬背了，真正從原理上理解！
以上就是最短路徑Dijkstra的圖示化證明是怎么樣的，小編相信有部分知識點可能是我們日常工作會見到或用到的。希望你能通過這篇文章學到更多知識。更多詳情敬請關注億速云行業資訊頻道。
免責聲明：本站發布的內容（圖片、視頻和文字）以原創、轉載和分享為主，文章觀點不代表本網站立場，如果涉及侵權請聯系站長郵箱：is@yisu.com進行舉報，并提供相關證據，一經查實，將立刻刪除涉嫌侵權內容。
