您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章將為大家詳細講解有關大數據中從概念到應用理解決策樹的示例分析,文章內容質量較高,因此小編分享給大家做個參考,希望大家閱讀完這篇文章后對相關知識有一定的了解。
盡管決策樹在機器學習中的使用已經存在了一段時間,但該技術仍然強大且受歡迎。向您展示如何構建決策樹,計算重要的分析參數以及繪制結果樹。

決策樹是我學到的流行且功能強大的機器學習算法之一。這是一種非參數監督學習方法,可用于分類和回歸任務。目的是創建一個模型,該模型通過學習從數據特征推斷出的簡單決策規則來預測目標變量的值。對于分類模型,目標值本質上是離散的,而對于回歸模型,目標值由連續值表示。與黑盒算法(例如神經網絡)不同, 決策樹 比較容易理解,因為它共享內部決策邏輯(您將在下一節中找到詳細信息)。
盡管許多數據科學家認為這是一種舊方法,但由于過度擬合的問題,他們可能對其準確性有所懷疑,但最近的基于樹的模型(例如,隨機森林(裝袋法),梯度增強(提升方法) )和XGBoost(增強方法)建立在決策樹算法的頂部。因此,決策樹 背后的概念和算法 非常值得理解!
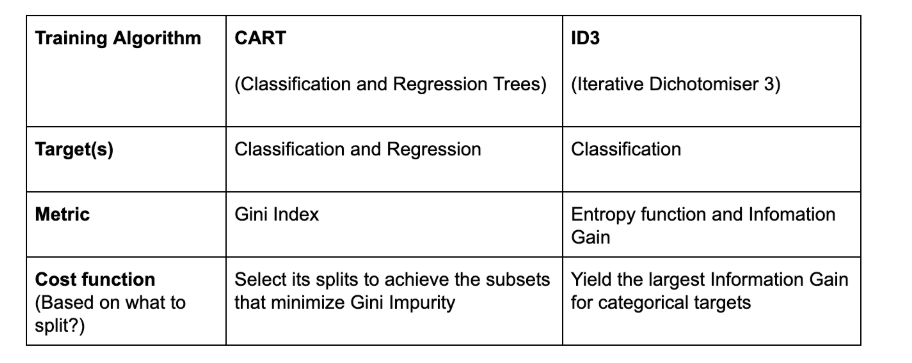
決策樹算法有4種流行類型: ID3, CART(分類樹和回歸樹), 卡方和 方差減少。
在此文章中,我將僅關注分類樹以及ID3和CART的說明。
想象一下,您每個星期日都打網球,并且每次都邀請您最好的朋友克萊爾(Clare)陪伴您。克萊爾有時會加入,但有時不會。對她而言,這取決于許多因素,例如天氣,溫度,濕度和風。我想使用下面的數據集來預測克萊爾是否會和我一起打網球。一種直觀的方法是通過決策樹。
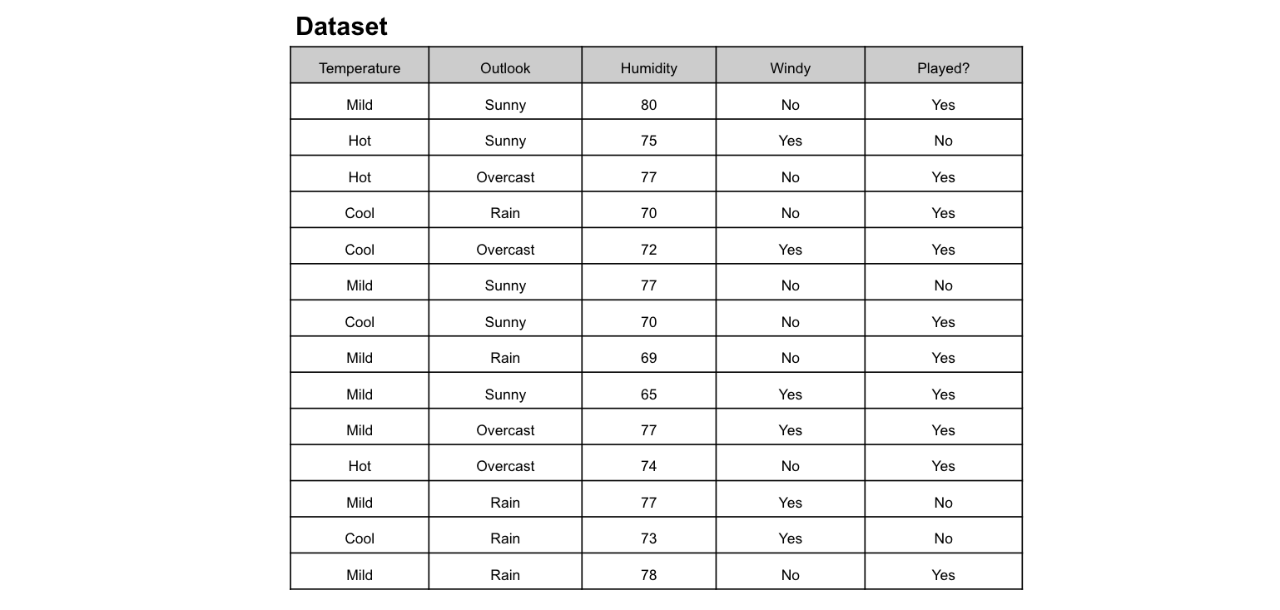
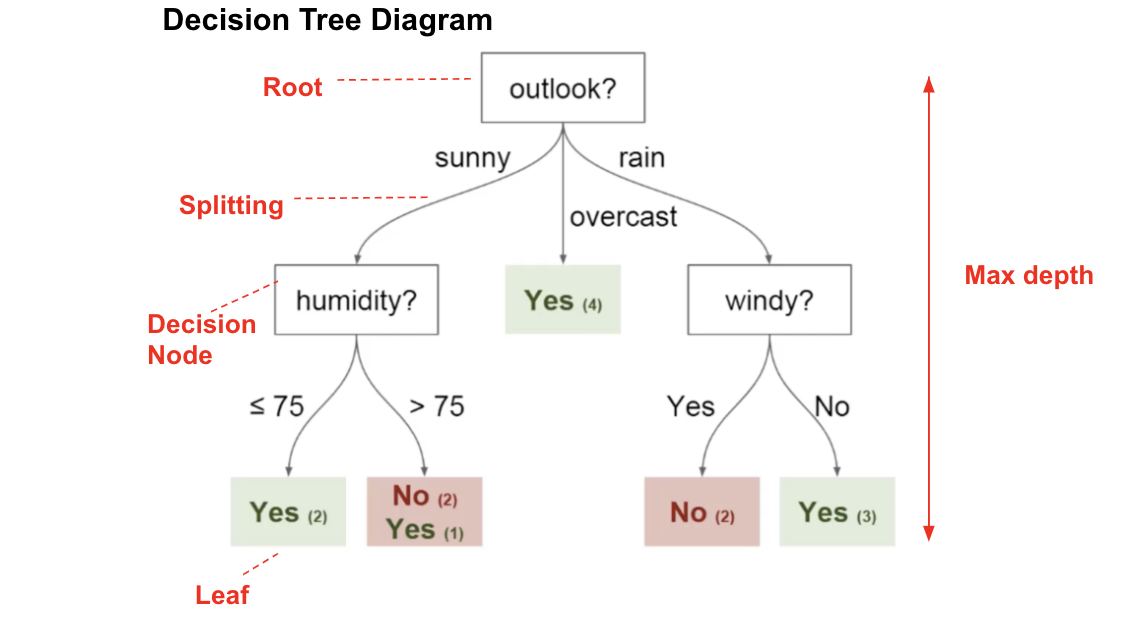
在此 決策樹 圖中,我們具有:
根節點:決定整個總體或樣本數據的第一個拆分應進一步分為兩個或更多同構集合。在我們的例子中,是Outlook節點。
拆分:這是將一個節點分為兩個或多個子節點的過程。
決策節點:該節點決定是否/何時將一個子節點拆分為其他子節點。在這里,我們有Outlook節點,Humidity節點和Windy節點。
葉子:預測結果(分類或連續值)的終端節點。有色節點(即“是”和“否”節點)是葉子。
問題:基于哪個屬性(功能)進行拆分?最佳分割是什么?
答:使用具有最高的屬性 信息增益 或 基尼增益
ID3決策樹算法使用信息增益來確定分裂點。為了衡量我們獲得了多少信息,我們可以使用 熵 來計算樣本的同質性。
問題:什么是“熵”?它的功能是什么?
答:這是對數據集中不確定性量的度量。 熵控制決策樹如何決定拆分 數據。它實際上影響決策樹如何 繪制邊界。
熵方程:

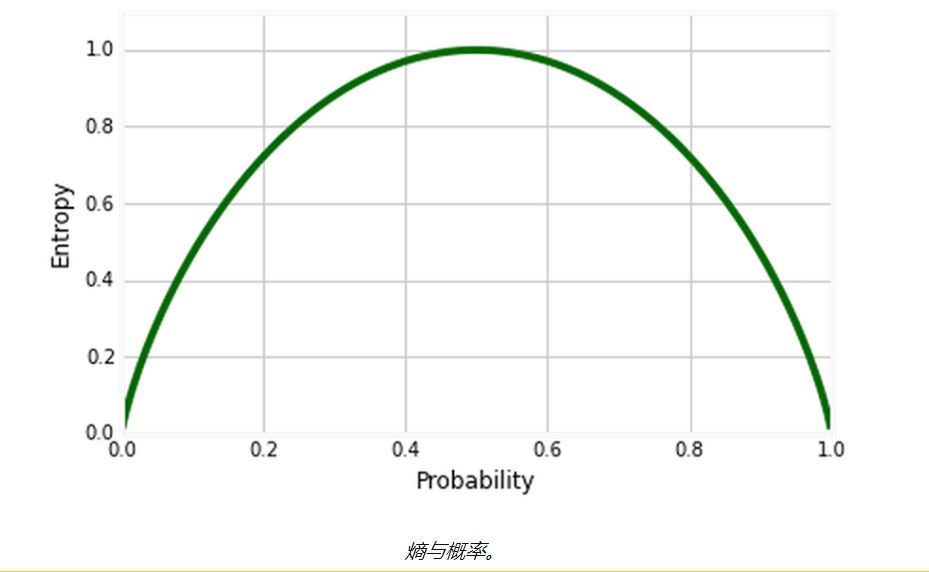
定義:決策樹中的熵代表同質性。
如果樣本是完全均勻的,則熵為0(概率= 0或1),并且如果樣本均勻地分布在各個類別中,則其熵為1(概率= 0.5)。
下一步是進行拆分,以最大程度地減少熵。我們使用 信息增益 來確定最佳拆分。
讓我向您展示在打網球的情況下如何逐步計算信息增益。在這里,我僅向您展示如何計算Outlook的信息增益和熵。
步驟1:計算一個屬性的熵—預測:克萊爾將打網球/克萊爾將不打網球
在此示例中,我將使用此列聯表來計算目標變量的熵:已播放?(是/否)。有14個觀測值(10個“是”和4個“否”)。'是'的概率(p)為0.71428(10/14),'否'的概率為0.28571(4/14)。然后,您可以使用上面的公式計算目標變量的熵。
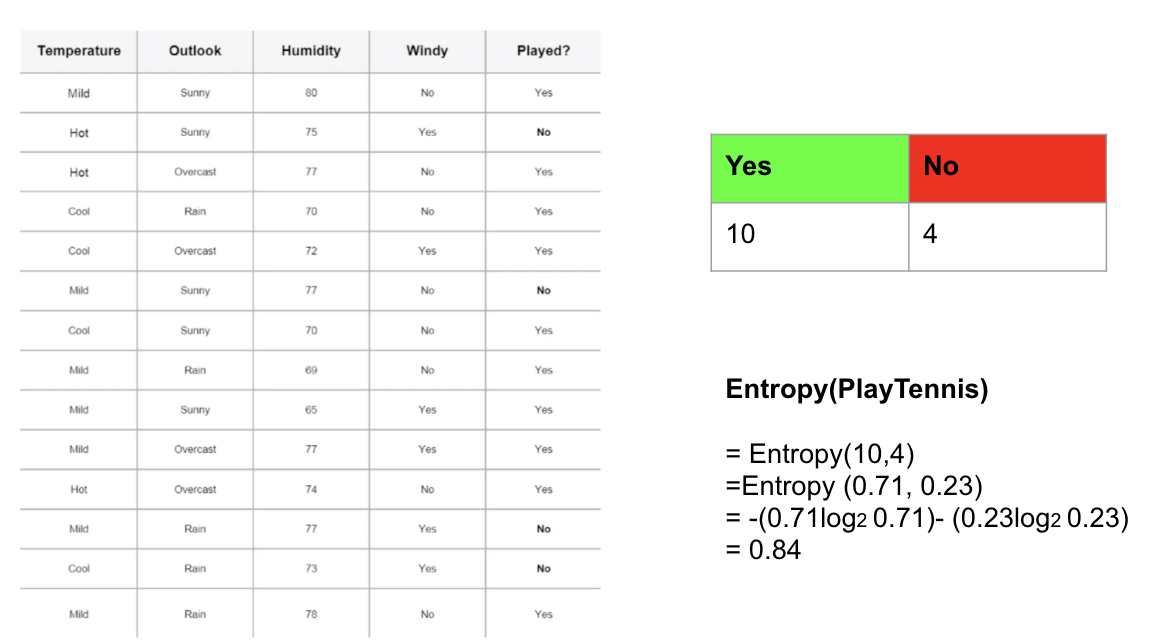
步驟2:使用列聯表計算每個特征的熵
為了說明這一點,我以Outlook為例,說明如何計算其熵。共有14個觀測值。匯總各行,我們可以看到其中5個屬于Sunny,4個屬于陰雨,還有5個屬于Rainy。因此,我們可以找到晴天,陰天和多雨的概率,然后使用上述公式逐一計算它們的熵。計算步驟如下所示。
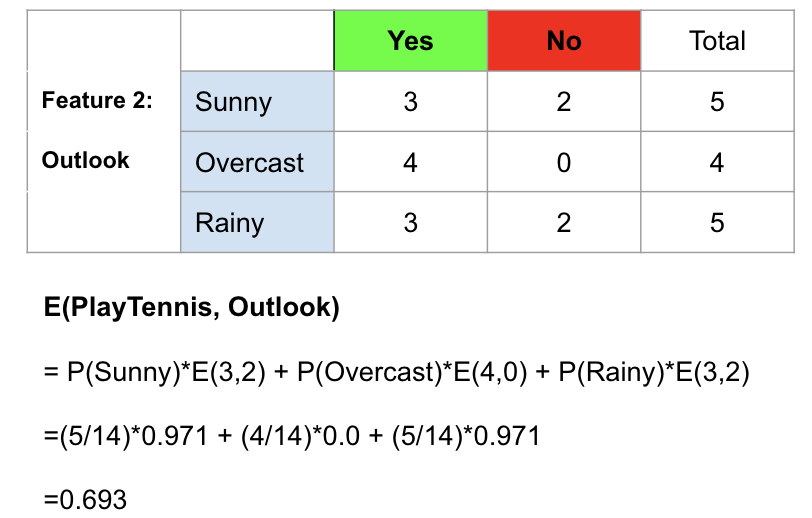
計算特征2(Outlook)的熵的示例。
定義:信息增益 是節點分裂時熵值的減少或增加。
信息增益方程式:
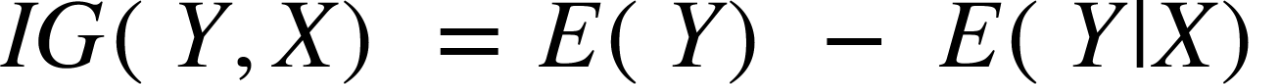
X在Y上獲得的信息

sklearn.tree。DecisionTreeClassifier: “熵”表示獲取信息
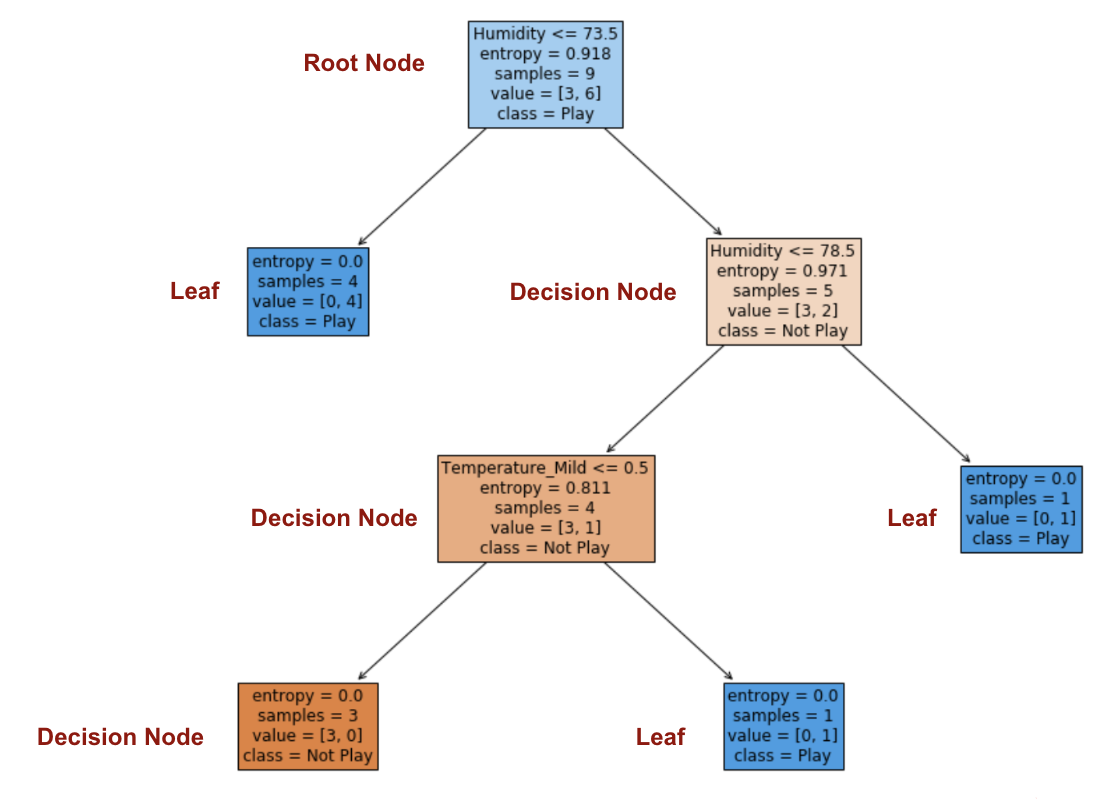
為了可視化如何使用信息增益構建決策樹 ,我僅應用了sklearn.tree。DecisionTreeClassifier 生成圖。
步驟3:選擇信息增益最大的屬性 作為根節點
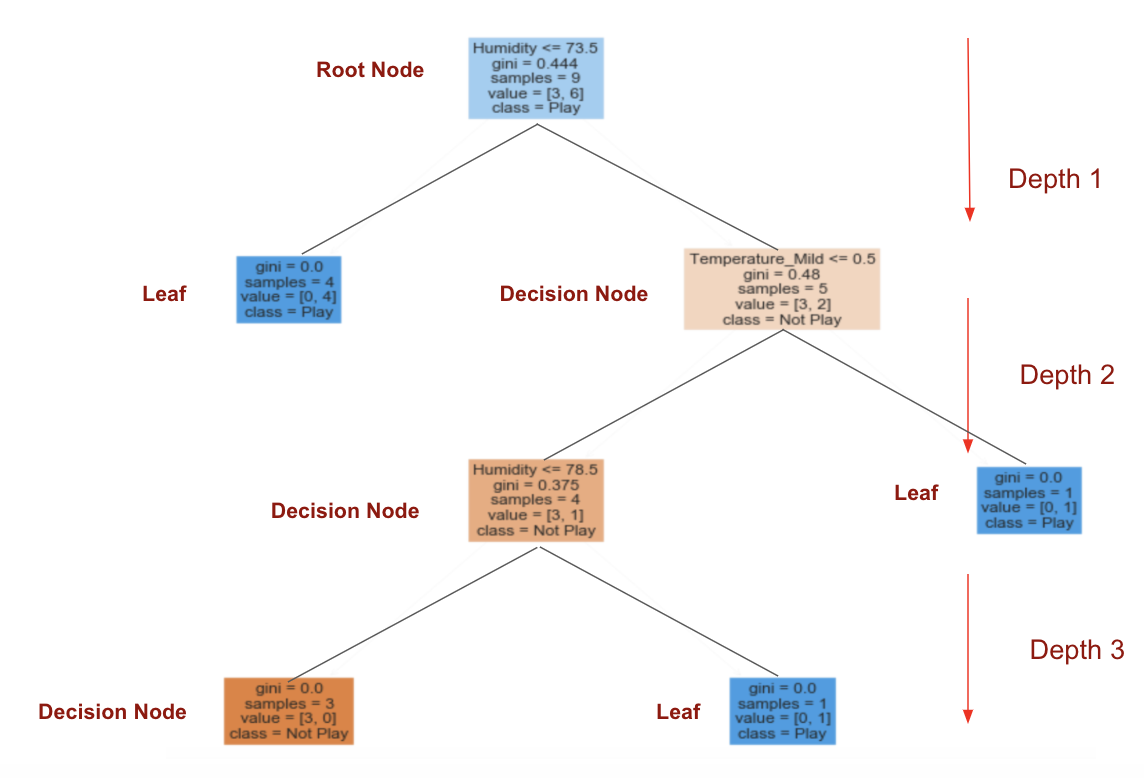
“濕度”的信息增益最高,為0.918。濕度是根節點。
步驟4: 熵為0的分支是葉節點,而熵大于0的分支需要進一步拆分。
步驟5:以ID3算法遞歸地增長節點,直到對所有數據進行分類。
您可能聽說過C4.5算法,對ID3的改進使用了“ 增益比” 作為信息增益的擴展。使用增益比的優點是通過使用Split Info標準化信息增益來處理偏差問題。在這里我不會詳細介紹C4.5。有關更多信息,請在此處簽出 (DataCamp)。
CART的另一種決策樹算法使用 Gini方法 創建分割點,包括Gini索引(Gini雜質)和Gini增益。
基尼系數的定義:通過隨機選擇標簽將錯誤的標簽分配給樣品的概率,也用于測量樹中特征的重要性。
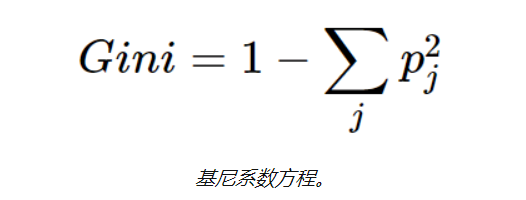

在為每個屬性計算Gini增益后,創建sklearn.tree。DecisionTreeClassifier 將選擇具有最大Gini增益的屬性 作為根節點。 甲 以0基尼分支是葉節點,而具有基尼分支大于0需要進一步分裂。遞歸地增長節點,直到對所有數據進行分類為止(請參見下面的詳細信息)。
如前所述,CART還可以使用不同的分割標準來處理回歸問題:確定分割點的均方誤差(MSE)。回歸樹的輸出變量是數字變量,輸入變量允許連續變量和分類變量混合使用。您可以通過DataCamp查看有關回歸樹的更多信息 。
大!您現在應該了解如何計算熵,信息增益,基尼系數和基尼增益!
問題:那么……我應該使用哪個?基尼系數還是熵?
答:通常,結果應該是相同的……我個人更喜歡基尼指數,因為它不涉及計算量更大的 日志 。但是為什么不都嘗試。
讓我以表格形式總結一下!
Scikit Learn 是針對Python編程語言的免費軟件機器學習庫。
步驟1:導入數據

步驟2:將分類變量轉換為虛擬變量/指標變量

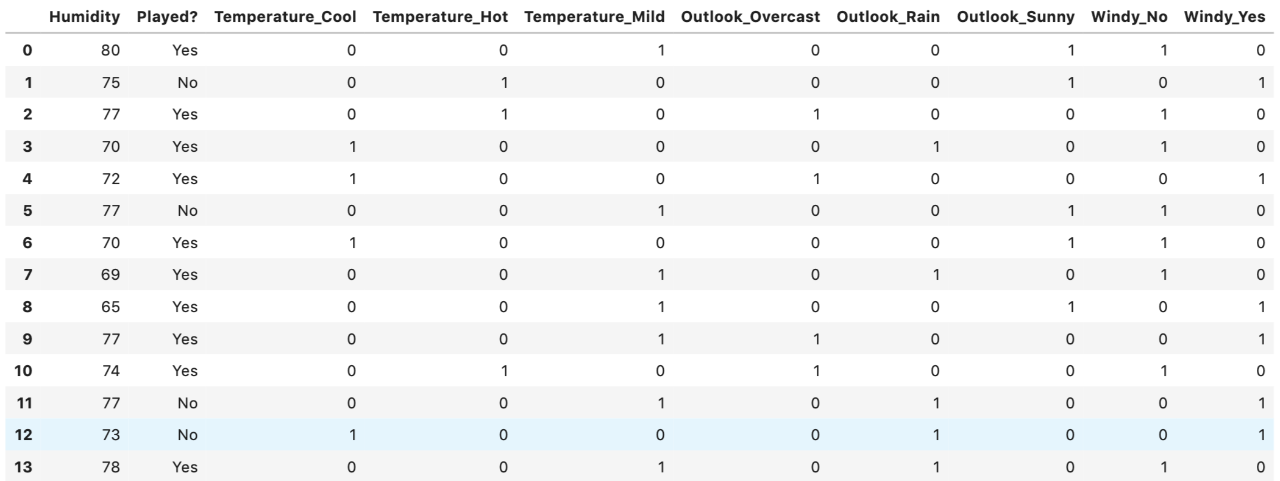
“溫度”,“ Outlook”和“風”的類別變量都轉換為虛擬變量。
步驟3:將訓練集和測試集分開

第4步:通過Sklean導入決策樹分類器

步驟5:可視化決策樹圖

有關代碼和數據集,請點擊此處查看。

為了提高模型性能(超參數優化),應調整超參數。有關更多詳細信息,請在 此處查看。
決策樹的主要缺點是過擬合,尤其是當樹特別深時。幸運的是,最近的基于樹的模型(包括隨機森林和XGBoost)建立在決策樹算法的頂部,并且它們通常具有強大的建模技術,并且比單個決策樹更具動態性,因此性能更好。因此,了解背后的概念和算法 決策樹 完全 是構建學習數據科學和機器學習打下良好的基礎超級有用。
關于大數據中從概念到應用理解決策樹的示例分析就分享到這里了,希望以上內容可以對大家有一定的幫助,可以學到更多知識。如果覺得文章不錯,可以把它分享出去讓更多的人看到。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。