您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“如何理解分布式系統中的哈希算法”,在日常操作中,相信很多人在如何理解分布式系統中的哈希算法問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”如何理解分布式系統中的哈希算法”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
Hash也稱散列、哈希,原理是把任意長度的字符串當作輸入,然后通過Hash算法變成固定長度輸出。Hash是一個映射的過程,因此是一定會產生沖突的,一般使用鏈地址法,開放尋址法等方法來解決hash沖突。
在分布式的情景下,為了解決數據和請求的定向問題,我們也會常常使用到哈希算法。接下來,就會介紹幾種常常在分布式環境下運用的hash算法。
哪怕是在分布式的環境下,我們也可以使用最簡單的hash算法,通過設定好每臺服務器對應的結果值,在請求或者數據進來時進行計算,將數據分別映射到相應的服務器上,由于計算規則是一致的,因此無論進行多少次的計算,數據的映射是不會進行變化的。
這種普通的哈希的方式優缺點分明,優點是實現簡單,清晰明了。缺點是由于分布式系統中的節點充滿了不確定性,可能會縮容或者擴容或者節點宕機,如果在這些情況下,意味著哈希的映射將會發生變化,同時之前的那些映射的數據需要進行遷移,以便之后能夠正確的訪問。而這種方式的哈希在這種情況下產生的數據遷移量將會是非常巨大的。
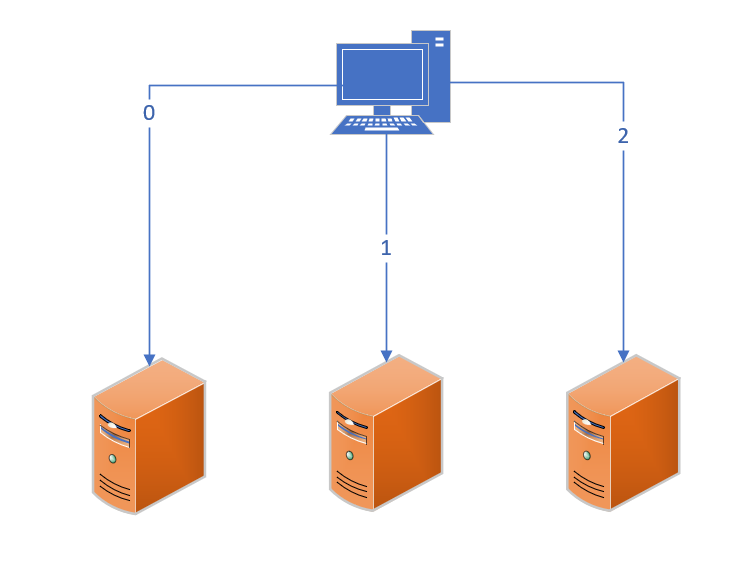
上圖是一個普通的分布式系統的哈希映射關系,3臺服務器分別接受哈希值為0,1,2的請求(一般為計算%2的值)。
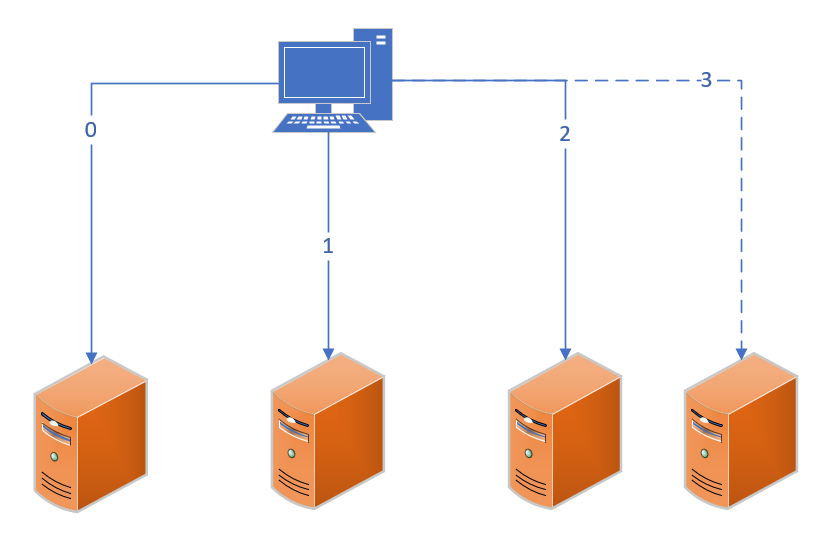
于是當我們新增一臺服務器之后,原本3臺服務器變成了4臺,哈希映射需要隨之修改,大量的數據需要遷移。
一致性哈希是為了解決之前說到的哈希造成的大量數據遷移的問題。
一致性哈希和普通哈希相比,同樣是有一定的映射關系的,但是不同的是,我們會在開始創建一個哈希環,在環上分布著大量的節點值,一般的范圍為0 ~ 2^32-1

之后我們會根據一定的規則,將服務器節點落在環上,如下圖
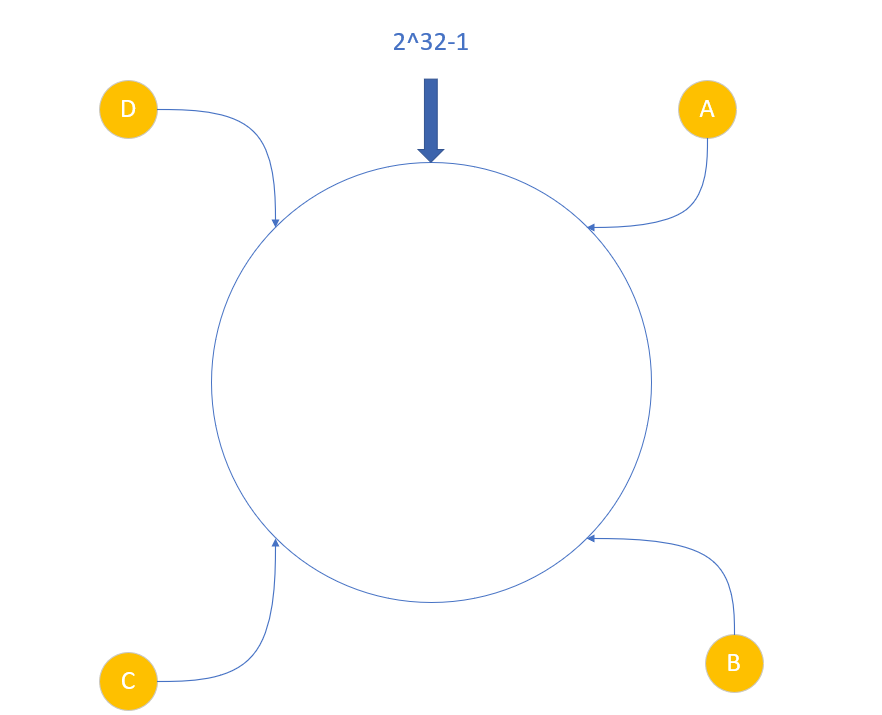
之后的邏輯就比較簡單了,當請求發往服務器后,經過計算找到其在環上的對應位置,然后檢查該位置上是否有對應服務器節點,如果有就將請求轉發過去,如果沒有就沿著哈希環順時針尋找,直到找到節點位置。
這樣設計的好處是顯而易見的,如果我們需要新增或者刪除節點的時候,每次只會影響至多2個節點的數據,相比較之前的普通哈希,消耗顯然是更少的。并且當某些服務器因故障突然宕機的時候,請求也可以順延到下個節點進行處理。
一致性哈希的特點決定了如果節點分布的不夠均勻會導致其中部分節點壓力過大,而部分節點有很多資源的空閑。如下圖
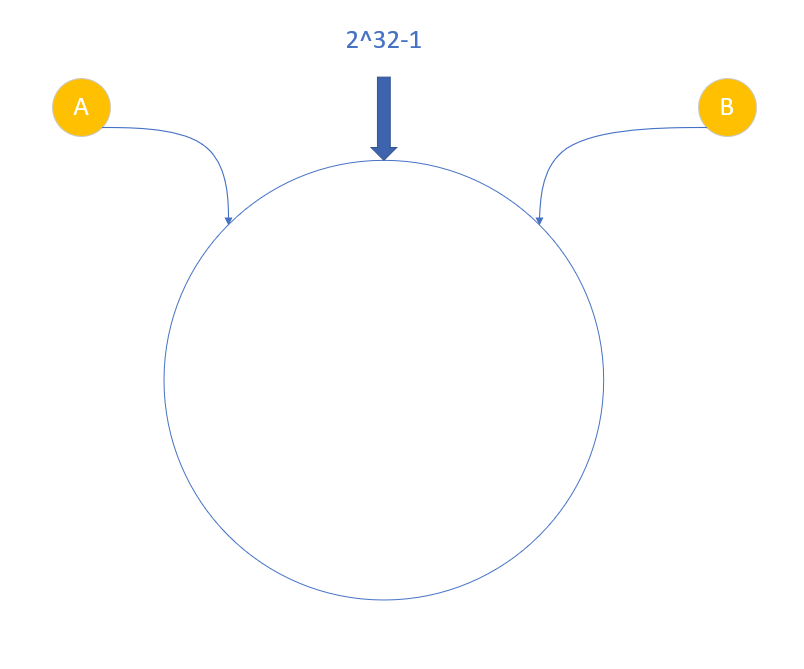
圖中的A,B節點顯然是不均衡的,請求會更多地發往A節點而B節點只能獲取A節點約1/3的請求。
于是一致性哈希往往會引入這么一個概念:虛擬節點。盡管我們的服務器分布不夠均勻,但是我們可以認為的創建一些虛擬節點,并且創建相應的映射,幫助虛擬節點把請求轉發到實際節點。
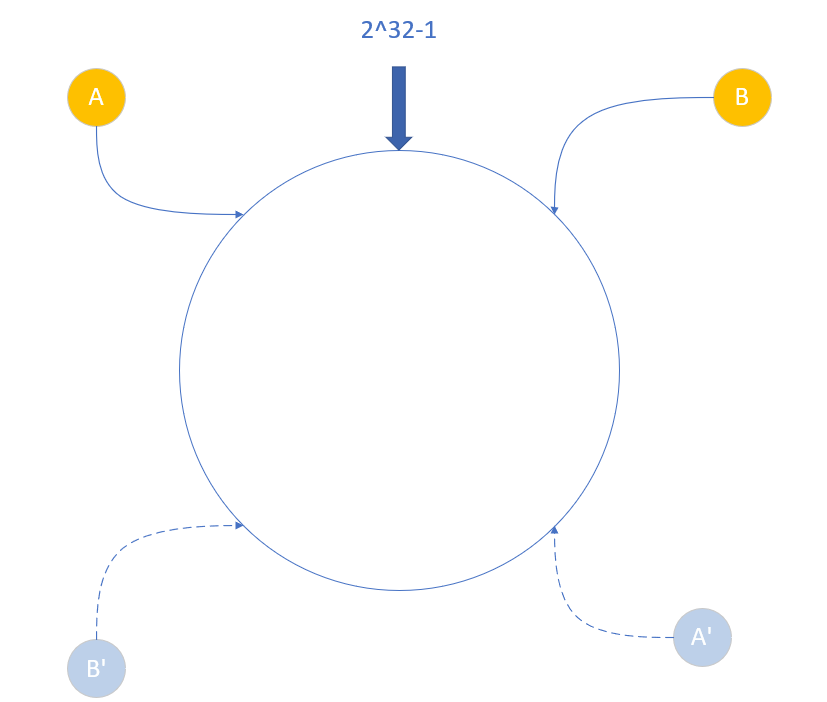
如圖,我們可以創建對應的虛擬節點A',B',然后把發往B'的請求轉發到B,A'的請求轉發到A,這樣就不會存在失衡的問題了。
哈希槽的典型是redis的分布式實現。
redis的分布式實現中,會在啟動集群的時候確認所有的服務器數量,然后將數量為16384的哈希槽平均分配給所有的master服務器,然后所有的數據都會存放在指定的節點之中。
redis的哈希槽的實現和一致性哈希有相同之處,也有不同之處。最主要的原因是redis采用了不同的高可用策略。一致性哈希在服務器宕機時會把流量轉到下一個服務器,但是redis不同,redis的集群模式會保證服務器節點擁有的主備模式。備份節點不會直接參與到哈希槽的分配中,但是當主節點宕機后,從節點會頂替主節點處理任務。
分布式哈希表(DHT)是一種分布式的哈希手段。和一致性哈希不同的是,DHT不需要中心節點來分配數據的流向。他有自己的一套機制保證無論數據剛開始走的是哪一個服務器,都可以找到自己需要前往的正確服務器。
Kademlia算法是一種典型的分布式的哈希表算法,多用于p2p網絡的構建,由Petar Maymounkov 和 David Mazieres共同創造。Kademlia論文源地址:Kademlia
分布式環境下的哈希表的難點在于以下幾點:
分布式環境下每個服務器不可能掌握所有服務器的情況,因此如何保證你的請求能在沒有中央節點定位的情況下找到對應的服務器是一大難點。
同樣由于分布式環境的服務器的掌握信息有限,那么服務器的加入和退出如何能夠被集群知曉也是一大難點。
那么我們來看Kademlia算法是如何解決這些問題的吧。
Kademlia使用到了異或來進行距離的計算。我們先來看看異或的定義。
異或的運算法則為:0⊕0=0,1⊕0=1,0⊕1=1,1⊕1=0(同為0,異為1)
然后我們來看看為什么用異或來計算距離。
a⊕b = b⊕a // 異或符合交換律,a節點到b節點的距離和b節點到a結點的距離相同 a⊕a = 0 // 自己和自己的距離為0 a⊕b >= 0 // 兩個節點之間的距離大于0 a⊕b + b⊕c >= a⊕c // a到b再到c的距離大于等于直接到c的距離
根據上述的一些異或的規則,我們可以發現異或和距離的一些特性可以說是絕配,真的很佩服算法的作者能夠想到如此精巧的設計。
確定了用異或來計算距離后,那么具體集群是如何構建并存儲信息使得可以查找到正確的信息呢?
Kademlia算法理論中每個集群的節點都會存儲一部分節點的信息(不可能存儲所有節點的信息,因為效率會低,并且無法保證實時性)。
所有的節點會構建成一棵獨特的二叉樹如下圖:
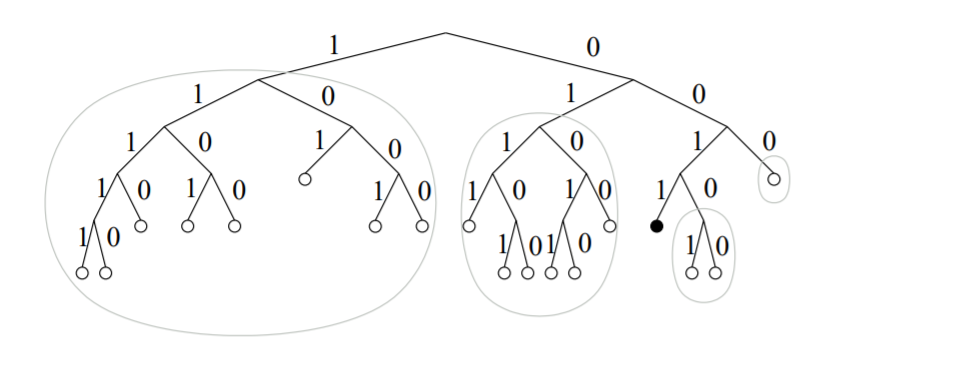
首先把每個節點的id經過一定的哈希計算得到該節點的一串01字符串以表示其在樹中的位置,從高位開始,1則往左子樹走,0往右子樹走,直到結束。可以看出圖中的黑色節點的哈希值為0011
Kademlia的二叉樹中的每一個節點都可以根據自己的視角進行二叉樹的拆分
拆分規則是從根節點開始依次把不包含自己的子樹拆分出來,以此類推,最后只剩下自己。之前的二叉樹拆分如之前的圖。對于黑色節點來說,外部有拆分出了四個不包含自己的子樹。
在二叉樹拆分之后每一個拆分過后的子樹實際上對應的就是一個一個bucket,每個bucket對于當前節點的距離是不同的范圍,距離越遠,高位不同,因此異或結果差距越大(距離越遠):
| K-bucket | 距離區間 |
|---|---|
| 0 | [2^0, 2^1) |
| 1 | [2^1, 2^2) |
| 2 | [2^2, 2^3) |
| 3 | [2^3, 2^4) |
| 4 | [2^4, 2^5) |
所以實際上每一個節點再進行拆分后只需要在對應的每個bucket中存儲一份該bucket的節點就可以遍歷整個二叉樹(集群)。當然為了容錯,一般來說每個bucket的節點都會保留幾個,而不僅僅是一個。
大致了解了原理之后,我們回過頭來看每次請求是如何定位節點的。
首先一個請求進入集群中的某個服務器。然后我們將請求帶著的目的地服務器的id和當前服務器的id計算兩者的距離。然后計算出了一個值,之后從服務器的bucket列表中尋找對應的bucket(即這個距離范圍對應的bucket)。我們的目標服務器就可以鎖定在了那個bucket的范圍之內,之后,在bucket中尋找距離該節點最近的K個服務節點(此參數可以自行設定大小),將請求重定向到這幾個節點。之后重復上述的步驟,如果該集群中真的有目標節點,那么就可以成功的返回。
基本的機制如此,當然在實際的環境中我們考慮到現實情況會對請求做超時處理,避免大量的節點間的查詢造成不必要的負載。
一個新節點是想加入網絡,首先有一個前提條件:他需要有一個處于網絡中的節點的信息,然后才能開啟加入流程。
加入流程:
新節點A以之前就有的節點T為起點,將其加入自己的K-bucket中,并且生成一個自己的節點id
節點A項節點B進行請求,以自己的id為參數請求節點定位自己的位置
之后就是查詢結點的流程了,每一個路經的節點都會找到自己節點中存儲的距離節點最近的節點,然后A把這些節點放入自己的bucket中以完善自己的路由表。同時,這些路經節點也會把A節點放入自己的路由表中,以待后用。
等到大部分節點返回后,A的路由表建立完成,一些節點也已經將A節點加入自己的路由表。至此A節點加入網絡成功。
算法中我們用到的一些參數其實是可以自己定義的:
k-bucket中的k:定義了每一層bucket會存儲k個節點信息
每一次請求會向s個節點發送信息
id的長度也是可以自定義的,注意id的長度會決定二叉樹的高度
到此,關于“如何理解分布式系統中的哈希算法”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。